An orientable manifold is a topological space that has a consistent choice of orientation throughout, allowing for the definition of volume and integration in a coherent manner. This property is crucial in fields like differential geometry and physics, where it ensures that vectors and tensors behave predictably under transformations. Explore the article to gain a deeper understanding of orientable manifolds and their significance in various mathematical contexts.
Table of Comparison
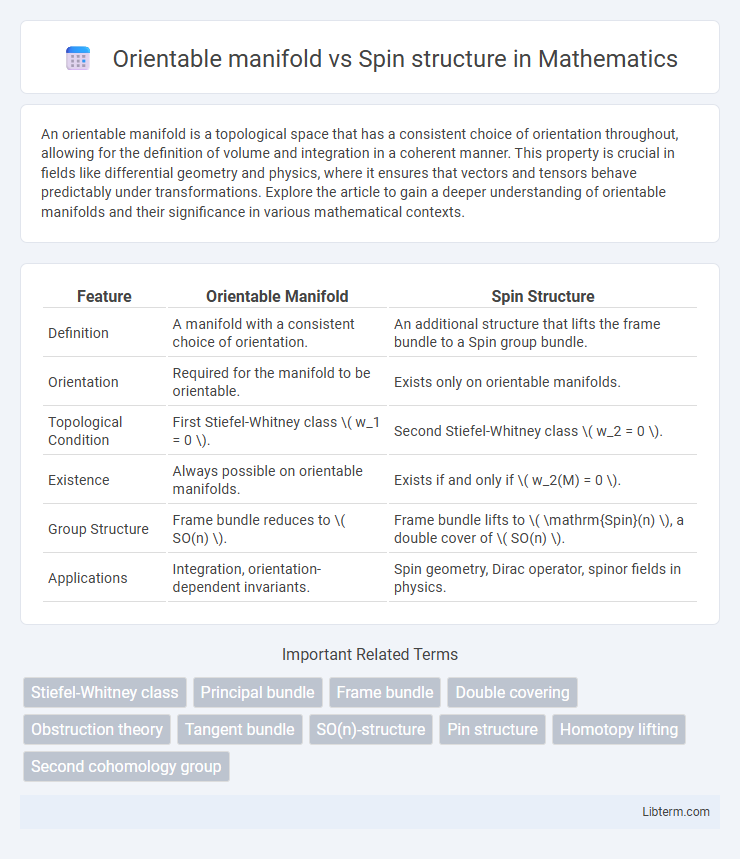
| Feature | Orientable Manifold | Spin Structure |
|---|---|---|
| Definition | A manifold with a consistent choice of orientation. | An additional structure that lifts the frame bundle to a Spin group bundle. |
| Orientation | Required for the manifold to be orientable. | Exists only on orientable manifolds. |
| Topological Condition | First Stiefel-Whitney class \( w_1 = 0 \). | Second Stiefel-Whitney class \( w_2 = 0 \). |
| Existence | Always possible on orientable manifolds. | Exists if and only if \( w_2(M) = 0 \). |
| Group Structure | Frame bundle reduces to \( SO(n) \). | Frame bundle lifts to \( \mathrm{Spin}(n) \), a double cover of \( SO(n) \). |
| Applications | Integration, orientation-dependent invariants. | Spin geometry, Dirac operator, spinor fields in physics. |
Introduction to Orientable Manifolds
An orientable manifold is a type of differentiable manifold that allows a consistent choice of orientation across its entire structure, which means it has a globally defined non-vanishing volume form. This property is fundamental in differential geometry and topology because it enables the definition of integrals and other orientation-dependent constructs on the manifold. Spin structures refine orientability by providing a lifting of the frame bundle to the Spin group, crucial for studying manifold properties in contexts like quantum field theory and index theorems.
Defining Spin Structures in Geometry
A spin structure on an orientable manifold is a lifting of its oriented orthonormal frame bundle from the special orthogonal group SO(n) to its double cover, the spin group Spin(n), enabling the consistent definition of spinor fields. Orientability ensures the reduction of the frame bundle to SO(n), which is a prerequisite for the existence of spin structures, characterized by a nontrivial second Stiefel-Whitney class w_2. The presence of a spin structure refines geometric and topological information beyond orientability, allowing the study of spin geometry and applications in quantum field theory and index theory.
Key Differences: Orientability vs Spin Structure
Orientable manifolds possess a consistent choice of orientation throughout the entire space, which means they admit a nowhere-vanishing top-dimensional form; this property is purely topological and ensures that one can define integration over the manifold. Spin structures, on the other hand, refine orientability by providing a lift of the frame bundle from the special orthogonal group SO(n) to its double cover Spin(n), allowing the definition of spinor fields crucial in quantum field theory and differential geometry. The key difference lies in that all manifolds admitting a spin structure are necessarily orientable, but not all orientable manifolds admit a spin structure, as the existence of a spin structure depends on vanishing of the second Stiefel-Whitney class \(w_2 = 0\), whereas orientability requires the first Stiefel-Whitney class \(w_1 = 0\).
Topological Requirements for Spin Structures
The topological requirement for a manifold to admit a Spin structure is that it must be orientable and its second Stiefel-Whitney class \(w_2\) must vanish. An orientable manifold has a trivial first Stiefel-Whitney class \(w_1 = 0\), ensuring the existence of an orientation. The absence of the obstruction \(w_2 = 0\) allows lifting the principal \(SO(n)\)-bundle of orthonormal frames to a principal \(Spin(n)\)-bundle, defining the Spin structure.
Examples of Orientable Manifolds Without Spin Structures
Certain orientable manifolds lack spin structures due to topological obstructions reflected in their second Stiefel-Whitney class, w2. A classic example is the complex projective plane CP2, which is orientable but does not admit a spin structure because w2(CP2) 0. Another example includes lens spaces L(p,q) with specific values of p and q, where despite orientability, the non-triviality of the second Stiefel-Whitney class prevents the existence of spin structures.
The Role of Stiefel-Whitney Classes
Stiefel-Whitney classes play a crucial role in distinguishing orientable manifolds from those admitting a spin structure by encoding topological obstructions. The first Stiefel-Whitney class \( w_1 \in H^1(M; \mathbb{Z}_2) \) detects orientability, where \( w_1 = 0 \) implies the manifold is orientable. The second Stiefel-Whitney class \( w_2 \in H^2(M; \mathbb{Z}_2) \) provides the obstruction to lifting the frame bundle to a spin structure; vanishing \( w_2 = 0 \) indicates the existence of a spin structure on an orientable manifold.
Spin Manifolds in Mathematical Physics
Spin manifolds, essential in mathematical physics, extend orientable manifolds by incorporating spin structures that allow the definition of spinor fields crucial for describing fermions in quantum field theory. A spin structure refines the orientability condition by lifting the frame bundle from the special orthogonal group SO(n) to its double cover Spin(n), enabling consistent formulation of spinor bundles and Dirac operators on the manifold. This additional structure is pivotal for the analysis of topological quantum field theories and the study of anomalies in gauge theories.
Applications in Topology and Geometry
Orientable manifolds form the fundamental framework in topology and geometry by enabling well-defined notions of direction and integration, crucial for classifying manifolds and studying their global properties. Spin structures refine orientability by allowing the definition of spinor fields, which are essential in understanding Dirac operators, index theory, and the topology of high-dimensional manifolds. Applications in geometry include the analysis of characteristic classes, the study of gauge theories, and the investigation of manifolds with special holonomy, where spin structures facilitate deeper insights into curvature and topological invariants.
Obstructions to Admitting a Spin Structure
An orientable manifold admits a consistent choice of orientation, but a Spin structure requires lifting the frame bundle to a Spin group, which introduces additional topological constraints. The primary obstruction to admitting a Spin structure on an orientable manifold is the second Stiefel-Whitney class \( w_2 \in H^2(M, \mathbb{Z}_2) \); the Spin structure exists if and only if \( w_2 = 0 \). Failure of \( w_2 \) to vanish prevents the manifold from having a Spin structure, highlighting a finer topological invariant beyond orientability.
Summary: Choosing Between Orientability and Spin Structure
An orientable manifold allows for a consistent choice of orientation across its entire surface, which is essential for defining volume forms and integration. A spin structure is a refinement that exists only on orientable manifolds with vanishing second Stiefel-Whitney class, enabling the definition of spinor fields critical in quantum field theory and differential geometry. Choosing between orientability and spin structure depends on the application's requirements, where orientability addresses basic topological consistency, while spin structure supports advanced geometric and physical frameworks.
Orientable manifold Infographic
 libterm.com
libterm.com