A projective variety is a fundamental concept in algebraic geometry, defined as the set of common zeros of a collection of homogeneous polynomials in a projective space. Its geometric structure reveals essential properties related to dimension, singularities, and morphisms, which are central to understanding complex algebraic varieties. Explore the rest of the article to discover how projective varieties shape modern geometric theories and their applications.
Table of Comparison
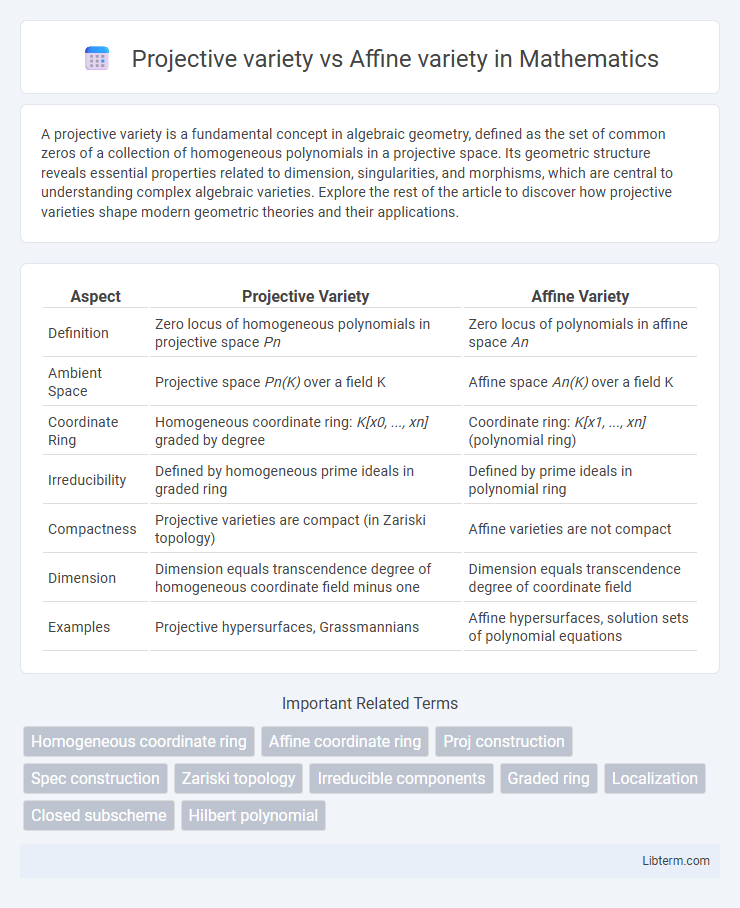
| Aspect | Projective Variety | Affine Variety |
|---|---|---|
| Definition | Zero locus of homogeneous polynomials in projective space Pn | Zero locus of polynomials in affine space An |
| Ambient Space | Projective space Pn(K) over a field K | Affine space An(K) over a field K |
| Coordinate Ring | Homogeneous coordinate ring: K[x0, ..., xn] graded by degree | Coordinate ring: K[x1, ..., xn] (polynomial ring) |
| Irreducibility | Defined by homogeneous prime ideals in graded ring | Defined by prime ideals in polynomial ring |
| Compactness | Projective varieties are compact (in Zariski topology) | Affine varieties are not compact |
| Dimension | Dimension equals transcendence degree of homogeneous coordinate field minus one | Dimension equals transcendence degree of coordinate field |
| Examples | Projective hypersurfaces, Grassmannians | Affine hypersurfaces, solution sets of polynomial equations |
Introduction to Algebraic Varieties
Affine varieties are solution sets of polynomial equations defined over affine space \(\mathbb{A}^n\), characterized by their coordinate rings that capture algebraic structures without points at infinity. Projective varieties extend affine varieties to projective space \(\mathbb{P}^n\), incorporating points at infinity and enabling a more comprehensive geometric framework that is invariant under scaling. The study of algebraic varieties involves analyzing these sets as geometric manifestations of polynomial ideals, with projective varieties providing compactifications of affine varieties critical for understanding their global properties.
Defining Affine Varieties
Affine varieties are algebraic sets defined as the common zeros of a set of polynomial equations within an affine space \(\mathbb{A}^n\). These varieties correspond to prime ideals in the polynomial ring \(k[x_1, \ldots, x_n]\), providing a direct algebraic-geometric correspondence via the Nullstellensatz. Unlike projective varieties, affine varieties are not compact and lack the homogeneous coordinate condition, which distinguishes their geometric and algebraic properties fundamentally.
What Are Projective Varieties?
Projective varieties are algebraic sets defined as the zero locus of homogeneous polynomials in projective space, which extends affine space by adding points at infinity to handle directions and ratios rather than just coordinates. Unlike affine varieties confined to \(\mathbb{A}^n\), projective varieties reside in \(\mathbb{P}^n\) and are crucial for studying properties invariant under projective transformations, such as degree and dimension. They provide a compactification framework essential for intersection theory, enabling a more complete geometric and topological analysis of algebraic varieties.
Key Differences: Projective vs Affine Varieties
Projective varieties are defined as the zero sets of homogeneous polynomials in projective space, whereas affine varieties arise from polynomial equations in affine space. Projective varieties include points at infinity, allowing for a compactification of affine varieties which do not inherently cover points at infinity. The key difference lies in their geometric settings and coordinate systems: projective varieties use homogeneous coordinates and capture global geometric properties, while affine varieties utilize standard coordinates focusing on local geometry.
Homogeneous Coordinates and Projective Space
Projective varieties are defined as the zero sets of homogeneous polynomials in projective space \( \mathbb{P}^n \), where points are represented by homogeneous coordinates \([x_0 : x_1 : \cdots : x_n]\) that are invariant under scalar multiplication. Affine varieties, on the other hand, correspond to zero sets of polynomials in affine space \( \mathbb{A}^n \), using standard coordinates \( (x_1, \ldots, x_n) \) without the projective scaling property. The use of homogeneous coordinates in projective varieties enables the compactification of affine varieties, allowing the study of geometric properties at infinity and ensuring compatibility with the projective transformations of \( \mathbb{P}^n \).
Charts, Coverings, and Localization
Projective varieties are defined by homogeneous polynomials in projective space and are covered by affine charts obtained through standard open subsets where a coordinate is nonzero, allowing local study via localization of their coordinate rings. Affine varieties correspond to zero sets of polynomials in affine space with a global coordinate ring, and their topology is given by Zariski open subsets that enable localization at prime ideals to analyze local properties. The key difference lies in projective varieties requiring multiple affine charts for cover and localization, while affine varieties have a single global chart and inherent localization in their coordinate ring structure.
Points at Infinity: Projective Completion
Projective varieties extend affine varieties by adding points at infinity, enabling a complete geometric description and resolving issues like parallel lines never intersecting. Affine varieties are defined by polynomial equations within affine space, lacking these points, while projective completion involves homogenizing these polynomials to embed the affine variety into projective space. This process ensures every projective variety includes the affine variety as a dense subset, with the added points embodying directions and limits at infinity.
Morphisms in Projective and Affine Varieties
Morphisms between affine varieties correspond to regular maps defined by polynomial functions, preserving the affine coordinate ring structure and allowing explicit algebraic descriptions. Projective variety morphisms involve homogeneous coordinate rings, with maps given by homogeneous polynomial functions that respect the projective equivalence classes, ensuring well-defined behavior on points at infinity. The distinction in morphisms reflects the underlying geometry: affine morphisms handle varieties embedded in affine space, while projective morphisms manage varieties in projective space, accommodating compactifications and global intersections.
Applications in Algebraic Geometry
Projective varieties, defined as zero sets of homogeneous polynomials in projective space, allow algebraic geometers to study properties invariant under scaling, facilitating the analysis of compactifications and intersections at infinity. Affine varieties, arising from polynomials over affine space, provide explicit coordinate descriptions suited for solving polynomial equations locally and computational applications like algorithmic algebraic geometry. The interplay between projective and affine varieties underpins key results in dimension theory, singularity analysis, and the classification of algebraic curves and surfaces.
Summary: Choosing Between Projective and Affine Approaches
Projective varieties offer a more complete geometric framework by including points at infinity, which resolves issues like intersection behavior and compactness absent in affine varieties. Affine varieties are simpler to handle computationally and are suitable for local or explicit calculations within Euclidean space. Choosing between projective and affine approaches depends on the problem's nature: projective methods excel in global geometric properties, while affine techniques are preferred for explicit algebraic computations.
Projective variety Infographic
 libterm.com
libterm.com