An algebraic set is a fundamental concept in algebraic geometry, defined as the collection of solutions to a system of polynomial equations over a given field. These sets can vary in complexity, encompassing anything from simple curves to higher-dimensional varieties, and their properties reveal deep connections between geometry and algebra. Explore the rest of the article to understand how algebraic sets shape the study of polynomial equations and geometric structures.
Table of Comparison
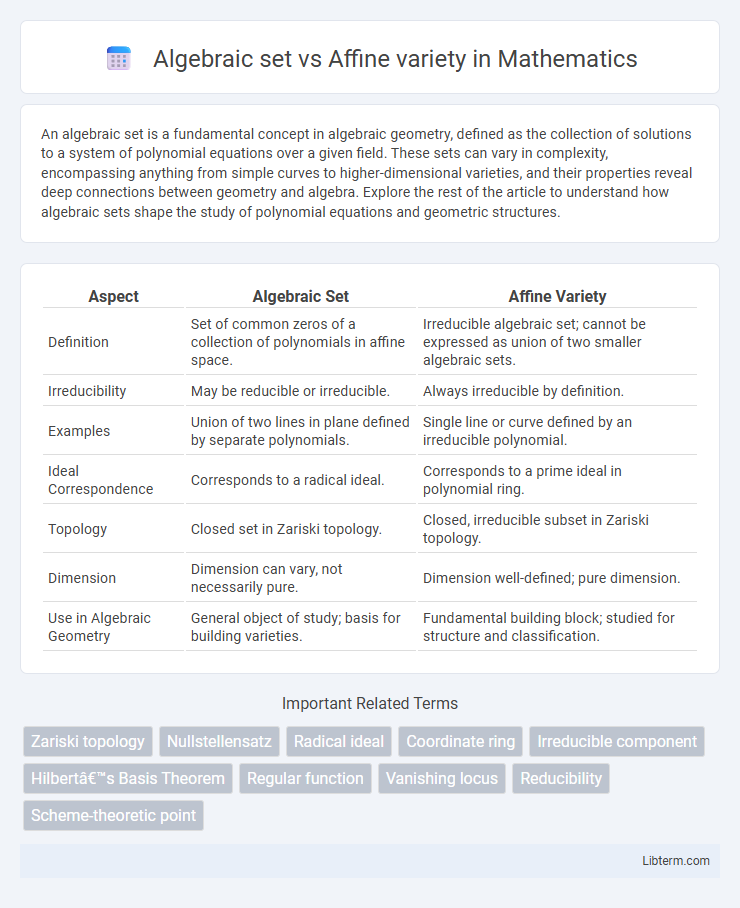
| Aspect | Algebraic Set | Affine Variety |
|---|---|---|
| Definition | Set of common zeros of a collection of polynomials in affine space. | Irreducible algebraic set; cannot be expressed as union of two smaller algebraic sets. |
| Irreducibility | May be reducible or irreducible. | Always irreducible by definition. |
| Examples | Union of two lines in plane defined by separate polynomials. | Single line or curve defined by an irreducible polynomial. |
| Ideal Correspondence | Corresponds to a radical ideal. | Corresponds to a prime ideal in polynomial ring. |
| Topology | Closed set in Zariski topology. | Closed, irreducible subset in Zariski topology. |
| Dimension | Dimension can vary, not necessarily pure. | Dimension well-defined; pure dimension. |
| Use in Algebraic Geometry | General object of study; basis for building varieties. | Fundamental building block; studied for structure and classification. |
Introduction to Algebraic Sets and Affine Varieties
Algebraic sets are the solution sets of polynomial equations in affine space, defined by the common zeros of a collection of polynomials over an algebraically closed field. Affine varieties are irreducible algebraic sets, meaning they cannot be expressed as the union of two smaller algebraic sets, and serve as the fundamental objects of study in algebraic geometry. The distinction between algebraic sets and affine varieties lies in reducibility, where affine varieties provide a more refined and structured approach to understanding geometric properties of polynomial equations.
Foundations of Algebraic Geometry
An algebraic set in algebraic geometry is defined as the set of common zeros of a collection of polynomials in affine space, serving as a fundamental object for studying solution loci. An affine variety is an irreducible algebraic set, meaning it cannot be expressed as the union of two smaller algebraic sets, providing a core building block in the classification of geometric structures. The distinction stems from foundational concepts like the Nullstellensatz, which links ideals in polynomial rings to algebraic sets, underpinning the correspondence between geometric objects and algebraic ideals.
Defining Algebraic Sets
Algebraic sets are defined as the solution sets of systems of polynomial equations over an algebraically closed field, forming the foundation for studying varieties in algebraic geometry. Affine varieties represent irreducible algebraic sets, meaning they cannot be expressed as the union of two smaller algebraic sets, highlighting their geometric and algebraic significance. Understanding these definitions is crucial for exploring the properties and classification of geometric objects in affine space.
Understanding Affine Varieties
Affine varieties are specific types of algebraic sets defined as the common zeros of a set of polynomials over an algebraically closed field, ensuring irreducibility and minimal polynomial description. Understanding affine varieties involves studying their geometric structure through coordinate rings and ideals, which correspond to the polynomial equations defining them. Unlike general algebraic sets, affine varieties are irreducible, meaning they cannot be written as a union of two smaller algebraic sets, highlighting their fundamental role in algebraic geometry.
Key Differences Between Algebraic Sets and Affine Varieties
Algebraic sets are defined as the common zeros of a collection of polynomials in an affine space, encompassing both reducible and irreducible components, whereas affine varieties specifically refer to irreducible algebraic sets. The key difference lies in irreducibility: affine varieties cannot be decomposed into simpler algebraic sets, while algebraic sets may be unions of several affine varieties. This distinction impacts their algebraic and geometric properties, influencing how solutions to polynomial equations are studied in algebraic geometry.
Zariski Topology and Its Role
Algebraic sets in affine space are subsets defined as the common zeros of a collection of polynomials, forming the closed sets in the Zariski topology. Affine varieties are irreducible algebraic sets, meaning they cannot be written as the union of two proper algebraic subsets, which corresponds to connected, irreducible closed sets under the Zariski topology. The Zariski topology's role is crucial as it provides the foundational framework to study algebraic sets and affine varieties, emphasizing their geometric and algebraic structures through its closed sets defined by polynomial vanishing.
Irreducibility in Algebraic Sets and Affine Varieties
Irreducibility in algebraic sets refers to a set that cannot be expressed as the union of two proper algebraic subsets, ensuring a single "piece" in the solution space. Affine varieties are prime examples of irreducible algebraic sets defined as the zero locus of a prime ideal in a polynomial ring, emphasizing their algebraic structure. Understanding this irreducibility distinction is crucial for studying geometric properties and decomposition within algebraic geometry.
The Importance of Coordinate Rings
Coordinate rings serve as fundamental algebraic objects that encapsulate the structure of algebraic sets and affine varieties, enabling a deeper understanding of their geometric properties through ring-theoretic methods. For an algebraic set, the coordinate ring is derived from the polynomial ring modulo the ideal of all polynomials vanishing on the set, while for an affine variety--a maximal algebraic set--the coordinate ring is an integral domain, reflecting the variety's irreducibility. Studying these coordinate rings allows for translating geometric problems into algebraic ones, facilitating classification, morphisms, and dimension theory within algebraic geometry.
Examples Illustrating Algebraic Sets vs Affine Varieties
An algebraic set in affine space is defined as the common zeros of a set of polynomials, such as the set of points satisfying \(x^2 + y^2 - 1 = 0\), representing a circle, which may include reducible components or singularities. In contrast, an affine variety is an irreducible algebraic set, exemplified by a parabola defined by \(y - x^2 = 0\), which cannot be decomposed into simpler algebraic sets. The distinction is critical in algebraic geometry, as algebraic sets can be unions of several varieties, while affine varieties serve as fundamental building blocks characterized by prime ideals in the coordinate ring.
Applications and Implications in Modern Mathematics
Algebraic sets form the foundational geometric objects defined as the common zeros of polynomial systems, playing a critical role in computational algebraic geometry and symbolic computation. Affine varieties, being irreducible algebraic sets, serve as essential building blocks in modern algebraic geometry, enabling precise classification and manipulation of solution spaces in areas such as cryptography, coding theory, and robotic motion planning. Their interplay profoundly impacts modern mathematical research, particularly in understanding geometric structures underlying polynomial equations and optimizing algorithms for solving systems of polynomial equations.
Algebraic set Infographic
 libterm.com
libterm.com