Topological properties focus on spatial relationships and continuity, examining how objects remain invariant under continuous transformations such as stretching or bending. This branch of mathematics plays a crucial role in various scientific fields, including physics, computer science, and biology, by helping to understand complex structures and systems. Dive into the rest of the article to explore how topological concepts can enhance Your knowledge and problem-solving skills.
Table of Comparison
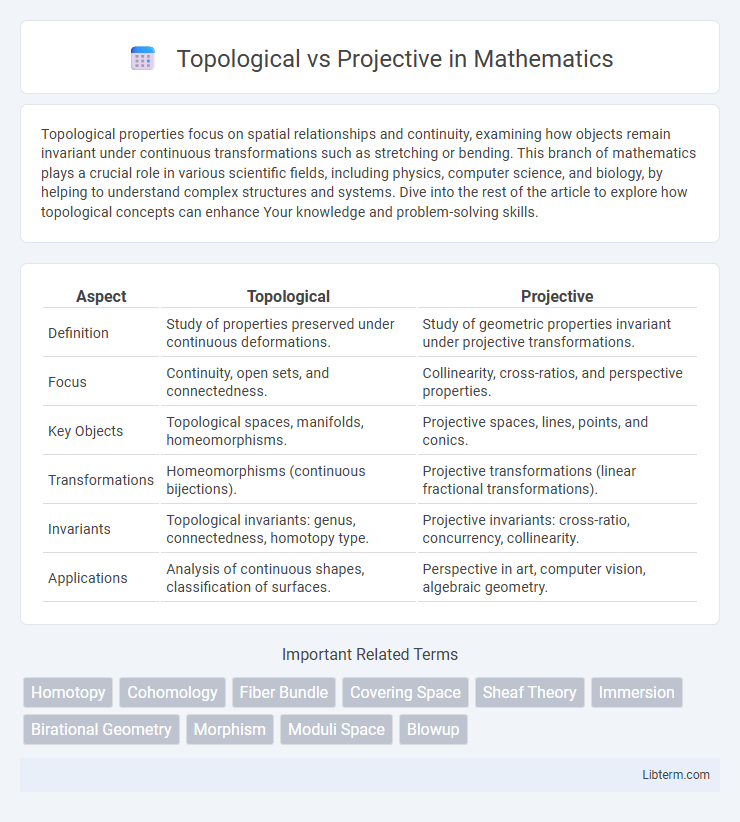
| Aspect | Topological | Projective |
|---|---|---|
| Definition | Study of properties preserved under continuous deformations. | Study of geometric properties invariant under projective transformations. |
| Focus | Continuity, open sets, and connectedness. | Collinearity, cross-ratios, and perspective properties. |
| Key Objects | Topological spaces, manifolds, homeomorphisms. | Projective spaces, lines, points, and conics. |
| Transformations | Homeomorphisms (continuous bijections). | Projective transformations (linear fractional transformations). |
| Invariants | Topological invariants: genus, connectedness, homotopy type. | Projective invariants: cross-ratio, concurrency, collinearity. |
| Applications | Analysis of continuous shapes, classification of surfaces. | Perspective in art, computer vision, algebraic geometry. |
Introduction to Topological and Projective Concepts
Topological concepts involve properties of space that are preserved under continuous deformations such as stretching or bending, emphasizing the study of open sets, continuity, and convergence. Projective concepts focus on properties invariant under projective transformations, involving elements like points, lines, and planes in projective geometry, where parallel lines meet at a point at infinity. Understanding the distinction between topological and projective frameworks is essential for applications in geometry, algebraic topology, and computer graphics.
Defining Topological Spaces
Topological spaces are defined by a set equipped with a topology, a collection of open sets satisfying union, finite intersection, and inclusion of the empty set and the entire space. Projective spaces, however, originate from linear algebra and geometry, constructed as the set of lines through the origin in a vector space, inheriting a topology from quotienting spheres or affine spaces. Understanding the defining structures of topological spaces clarifies their role in continuity, convergence, and boundary concepts, differentiating them fundamentally from projective spaces used in geometric transformations and perspectives.
Understanding Projective Spaces
Projective spaces extend topological spaces by incorporating points at infinity, enabling the treatment of lines intersecting at a common point without exceptions. Unlike purely topological spaces, projective spaces are characterized by homogeneous coordinates and equivalence classes, which provide a framework for studying geometric properties invariant under projection. Understanding projective spaces is crucial for applications in algebraic geometry, computer vision, and complex analysis, where transformations and intersections require a comprehensive model beyond Euclidean constraints.
Historical Evolution of Topological vs Projective Approaches
The historical evolution of topological and projective approaches reveals distinct mathematical paradigms, with topology emerging in the late 19th century focused on properties preserved under continuous deformations. Projective geometry, rooted in the Renaissance era and formalized during the 19th century, centers on invariants under projection and perspective transformations. This divergence reflects differing aims: topology addresses qualitative spatial properties, while projective geometry emphasizes relations invariant under projection, shaping modern mathematical and geometric theories.
Fundamental Differences Between Topological and Projective Properties
Topological properties refer to features of a space that remain invariant under continuous deformations such as stretching or bending, including connectedness and compactness. Projective properties arise from projective geometry and involve invariants under projective transformations, focusing on properties like collinearity and cross-ratio that are preserved under projection. Unlike topological properties concerned with intrinsic spatial relations, projective properties emphasize perspective and alignment aspects in geometric figures.
Key Applications in Mathematics and Physics
Topological methods are crucial in studying properties preserved under continuous deformations, making them fundamental in areas like algebraic topology, quantum field theory, and condensed matter physics for analyzing phase transitions and spatial properties. Projective geometry plays a key role in computer graphics, perspective theory, and string theory, where it facilitates the understanding of transformations, invariants, and compactified dimensions. The interplay between topological invariants and projective spaces enables advancements in modern physics, particularly in gauge theories and the classification of quantum states.
Advantages and Limitations of Topological Methods
Topological methods excel in capturing intrinsic geometric properties invariant under continuous deformations, facilitating robust analysis in fields like data science, robotics, and network theory. Their advantages include stability to noise, the ability to identify global features such as holes and connected components, and applicability to high-dimensional data without embedding constraints. Limitations arise from computational complexity in large datasets, challenges in interpreting abstract topological invariants, and potential loss of metric information critical for certain applications.
Benefits and Challenges of Projective Techniques
Projective techniques unlock deeper insights by revealing unconscious attitudes and emotions, making them valuable in market research and psychology for accessing hidden motivations. Their benefits include eliciting genuine responses and enabling creativity, but challenges arise from subjective interpretation, requiring skilled analysts to avoid bias. Projective methods often demand more time and resources, complicating standardization and quantitative analysis compared to topological approaches.
Real-World Examples: Topological vs Projective Models
Topological models emphasize properties preserved under continuous deformations, such as stretching or bending, making them ideal for analyzing networks like social connections or transportation systems where connectivity matters more than precise distances. Projective models focus on properties invariant under projection transformations, particularly useful in computer vision and graphics for rendering 3D scenes onto 2D planes, as seen in camera imaging or architectural blueprints. Real-world applications demonstrate topological models in urban transit mapping, while projective models underpin perspective illusions in art and photogrammetry.
Conclusion: Choosing Between Topological and Projective Perspectives
Selecting between topological and projective perspectives depends on the specific goals of your analysis; topological approaches emphasize the intrinsic connectivity and continuity of structures, while projective methods highlight spatial relationships and perspectives. Topological models are optimal for understanding properties invariant under continuous transformations, whereas projective perspectives excel in applications involving perspective, projection, and visual representation. The decision should align with whether the focus is on abstract structural properties or on spatial geometry and visualization contexts.
Topological Infographic
 libterm.com
libterm.com