Pure Hodge structures provide a fundamental framework in algebraic geometry, characterizing the decomposition of cohomology groups of smooth projective varieties into complex subspaces with specific weight and Hodge filtrations. These structures are essential to understanding the interplay between topology and complex analysis, revealing deep insights about the geometric and arithmetic properties of varieties through Hodge theory. Explore the rest of this article to uncover the intricate details and applications of pure Hodge structures in modern mathematics.
Table of Comparison
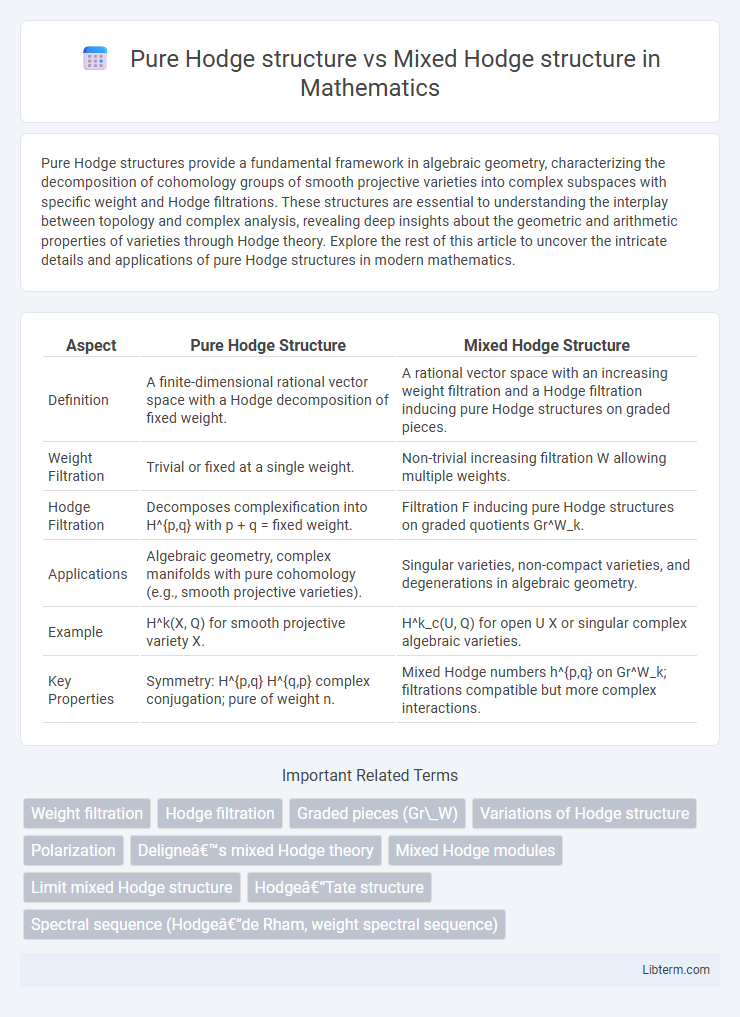
| Aspect | Pure Hodge Structure | Mixed Hodge Structure |
|---|---|---|
| Definition | A finite-dimensional rational vector space with a Hodge decomposition of fixed weight. | A rational vector space with an increasing weight filtration and a Hodge filtration inducing pure Hodge structures on graded pieces. |
| Weight Filtration | Trivial or fixed at a single weight. | Non-trivial increasing filtration W allowing multiple weights. |
| Hodge Filtration | Decomposes complexification into H^{p,q} with p + q = fixed weight. | Filtration F inducing pure Hodge structures on graded quotients Gr^W_k. |
| Applications | Algebraic geometry, complex manifolds with pure cohomology (e.g., smooth projective varieties). | Singular varieties, non-compact varieties, and degenerations in algebraic geometry. |
| Example | H^k(X, Q) for smooth projective variety X. | H^k_c(U, Q) for open U X or singular complex algebraic varieties. |
| Key Properties | Symmetry: H^{p,q} H^{q,p} complex conjugation; pure of weight n. | Mixed Hodge numbers h^{p,q} on Gr^W_k; filtrations compatible but more complex interactions. |
Introduction to Hodge Structures
Hodge structures provide a powerful framework in algebraic geometry and complex analysis, encoding information about the cohomology of smooth projective varieties through a decomposition into subspaces indexed by pairs of integers. Pure Hodge structures arise from smooth projective varieties and exhibit a single weight filtration, reflecting a uniform level of complexity in cohomological data. Mixed Hodge structures generalize this concept to include singular or non-compact varieties, featuring multiple weight filtrations that capture intricate layers of topological and geometric information.
What Is a Pure Hodge Structure?
A pure Hodge structure is a mathematical framework in algebraic geometry and complex analysis characterized by a finite-dimensional complex vector space with a decomposition into subspaces indexed by pairs of integers (p, q) that satisfies specific symmetry properties, reflecting the geometric and topological features of smooth projective varieties. This decomposition, called the Hodge decomposition, encodes the cohomology of a smooth projective variety with each piece corresponding to harmonic forms of type (p, q), leading to a pure Hodge structure of weight n when the sum p + q equals n. Pure Hodge structures are fundamental in understanding the Hodge theory of smooth projective varieties, providing a rich interplay between complex geometry, topology, and number theory.
Properties and Examples of Pure Hodge Structures
Pure Hodge structures are characterized by a decomposition of the complexified cohomology group into a direct sum of subspaces \( H^{p,q} \) where \( p+q = n \), with \( n \) being the fixed weight, and satisfying the condition \( \overline{H^{p,q}} = H^{q,p} \). Key properties include the purity of the Hodge filtration and compatibility with complex conjugation, making them fundamental in the study of Kahler manifolds and smooth projective varieties. Examples of pure Hodge structures arise naturally from the singular cohomology groups of smooth projective algebraic varieties, such as the classical Hodge decomposition on the cohomology of complex algebraic curves or surfaces.
Defining Mixed Hodge Structures
Mixed Hodge structures extend pure Hodge structures by allowing a finite increasing weight filtration alongside the decreasing Hodge filtration, encoding more complex geometrical and topological data. Unlike pure Hodge structures characterized by a single weight with decomposition into (p,q)-components, mixed Hodge structures accommodate singularities and non-compact spaces through successive graded pieces of pure Hodge structures. This sophisticated framework was developed to analyze the cohomology of arbitrary algebraic varieties, blending algebraic, differential, and topological methods.
Filtrations in Mixed Hodge Theory
In Mixed Hodge Theory, filtrations play a crucial role in defining Mixed Hodge structures, characterized by two increasing filtrations: the weight filtration \(W_\bullet\) and the Hodge filtration \(F^\bullet\). The weight filtration \(W_\bullet\) is an increasing filtration on a rational vector space that reflects the complexity or "mixedness" of the structure, while the Hodge filtration \(F^\bullet\) provides a decreasing filtration on the complexification compatible with the weight filtration, encoding the pure Hodge decomposition on graded pieces \( \mathrm{Gr}^W_n \). Unlike Pure Hodge structures, which only involve a single Hodge filtration satisfying the Hodge decomposition on a fixed weight, Mixed Hodge structures require the interplay between both filtrations to capture phenomena in the cohomology of singular or non-compact algebraic varieties.
Key Differences: Pure vs. Mixed Hodge Structures
Pure Hodge structures consist of a single weight with a decomposition of complexified cohomology into Hodge components \(H^{p,q}\) satisfying \(p + q = n\), whereas Mixed Hodge structures involve a filtration by weights allowing multiple weights to coexist, reflecting more complex geometric or topological features. Pure structures appear in smooth, projective varieties, while mixed structures naturally arise in singular or non-compact varieties, capturing additional layers of complexity. The key difference lies in the presence of a weight filtration in mixed Hodge structures absent in pure Hodge structures, enabling a finer analysis of the associated cohomological data.
Applications in Algebraic Geometry
Pure Hodge structures are fundamental in understanding the cohomology of smooth projective varieties, offering a clear decomposition of cohomology groups that reflects complex geometric properties. Mixed Hodge structures extend these ideas to singular or non-compact varieties, enabling the study of cohomological invariants in more general algebraic geometric contexts, such as degenerations and resolutions. Applications include analyzing the topology of algebraic varieties, studying variations of Hodge structures in moduli problems, and providing tools for the decomposition theorems and weight filtrations critical in modern algebraic geometry.
Role in Cohomology and Topology
Pure Hodge structures arise in the study of smooth projective varieties and provide a direct decomposition of cohomology groups into types (p,q), reflecting the algebraic and topological properties of these varieties. Mixed Hodge structures extend this framework to singular or non-compact varieties, capturing more complex topological features through a weight filtration combined with the Hodge filtration. Both structures play a crucial role in understanding the topology of algebraic varieties by encoding how cohomology groups vary with geometric singularities and compactifications.
Recent Advances and Research Directions
Recent advances in Hodge theory emphasize the intricate interplay between pure and mixed Hodge structures, particularly in understanding degenerations of algebraic varieties and their cohomological properties. Cutting-edge research explores the extension of pure Hodge structures to mixed settings, leveraging tools like the weight filtration and limiting mixed Hodge structures to analyze singularities and moduli problems. Emerging directions focus on categorical and motivic aspects, enhancing the application of mixed Hodge theory in arithmetic geometry and mirror symmetry.
Conclusion: Comparing Pure and Mixed Hodge Structures
Pure Hodge structures exhibit a well-defined, single-weight grading, facilitating clear decompositions of cohomology groups into Hodge components with fixed weights, essential for understanding smooth projective varieties. Mixed Hodge structures, by contrast, incorporate a filtration by weights allowing components of varying weights, which is crucial for studying singular or non-compact algebraic varieties with more complex topology. The comparison reveals that mixed Hodge structures generalize pure ones, providing a powerful framework to capture geometric and topological nuances beyond the scope of pure Hodge theory.
Pure Hodge structure Infographic
 libterm.com
libterm.com