The universal set encompasses all elements under consideration within a particular discussion or problem, serving as the foundational basis for set theory operations. It includes every possible member relevant to a specific context, allowing for clear definitions of subsets, complements, and intersections. Explore the rest of the article to deepen Your understanding of how the universal set functions in various mathematical and practical applications.
Table of Comparison
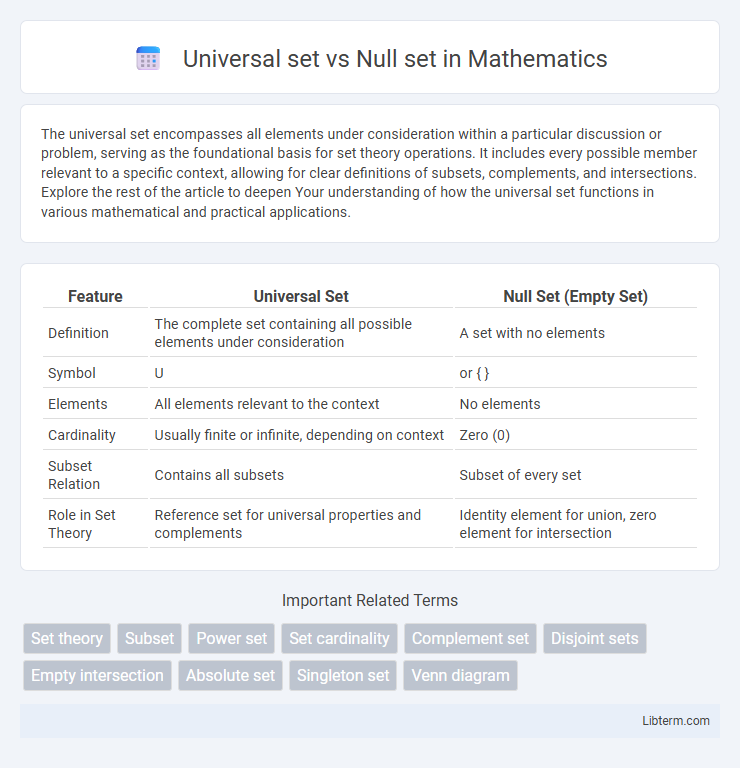
| Feature | Universal Set | Null Set (Empty Set) |
|---|---|---|
| Definition | The complete set containing all possible elements under consideration | A set with no elements |
| Symbol | U | or { } |
| Elements | All elements relevant to the context | No elements |
| Cardinality | Usually finite or infinite, depending on context | Zero (0) |
| Subset Relation | Contains all subsets | Subset of every set |
| Role in Set Theory | Reference set for universal properties and complements | Identity element for union, zero element for intersection |
Introduction to Universal Set and Null Set
The Universal Set, often denoted by U, contains all possible elements under consideration within a particular discussion or problem domain, serving as the foundational reference for set theory operations. The Null Set, also known as the Empty Set and represented by , is a unique set that contains no elements, highlighting the concept of emptiness or absence within the universal context. Understanding both the Universal Set and Null Set is essential for grasping the fundamentals of subsets, complements, and set relations in mathematical logic and theory.
Definitions: Universal Set vs Null Set
The universal set, often denoted by U, contains all elements under consideration in a particular discussion or problem domain, while the null set, also known as the empty set and denoted by , contains no elements at all. The universal set serves as the complete reference set from which subsets are derived, whereas the null set represents the unique subset that contains zero elements. These foundational definitions establish the universal set as the superset of all possible elements and the null set as the minimal subset with an absence of elements.
Notation and Symbols Used
The universal set is commonly denoted by the symbol \( U \) and contains all possible elements under consideration, serving as the reference set in set theory. The null set, also called the empty set, is represented by the symbol \( \emptyset \) or \( \{\} \) and contains no elements. These notations are fundamental in expressing relationships such as complements, intersections, and unions within the framework of sets.
Properties of the Universal Set
The Universal set, denoted by U, contains all possible elements under consideration within a particular discussion or problem, making it the superset of every other set including the Null set, which contains no elements. Key properties of the Universal set include its status as the identity element for intersection operations, where the intersection of U with any set A equals A itself (U A = A), and its role as the absorbing element in unions, where the union of U with any set equals U (U A = U). The Universal set is also unique in that every set is a subset of U, and its complement in itself is the Null set, symbolized as U = .
Properties of the Null Set
The null set, also known as the empty set, contains no elements and is a subset of every set, including the universal set. Its cardinality is zero, meaning it has no members, and it plays a crucial role in set theory as the identity element for the union operation. The null set is unique, denoted by , and does not affect the membership status of other elements in operations involving sets.
Differences Between Universal Set and Null Set
The universal set contains all possible elements under consideration within a particular context, while the null set, or empty set, contains no elements at all. The universal set is often denoted by the symbol U or x, encompassing every member of the domain, whereas the null set is represented by or {}. In set theory, the null set is a subset of every set, including the universal set, highlighting their fundamental difference in element inclusion and scope.
Relationship with Other Sets
The universal set contains all elements under consideration, making every other set a subset within it, while the null set, or empty set, contains no elements and is a subset of every set, including the universal set. The relationship between these sets forms the foundation for set operations and logic, as the null set represents the absence of elements and the universal set represents the complete collection. In set theory, intersections involving the null set always result in the null set, and unions with the universal set always result in the universal set.
Examples of Universal Set and Null Set
The universal set includes all possible elements within a particular context, such as the set of all natural numbers {1, 2, 3, ...} when discussing number theory, whereas the null set or empty set contains no elements, denoted as or {}. For example, in the study of geometric shapes, a universal set can be defined as all polygons, while the null set might be the set of polygons with exactly five sides and exactly six sides simultaneously, which is impossible and thus empty. In probability theory, if the universal set represents all outcomes of rolling a six-sided die {1, 2, 3, 4, 5, 6}, then the null set could represent rolling a seven, an event with no outcomes.
Applications in Set Theory and Mathematics
The Universal set contains all objects or elements under consideration, serving as the foundational domain in set theory, while the Null set (empty set) contains no elements, representing the absence of objects. In mathematical proofs, the Universal set provides a reference space for defining complements and relative sets, whereas the Null set is crucial in concepts like intersections and limits where the result is an empty collection. Applications in probability theory and logic utilize the Null set to denote impossible events and contradictions, whereas the Universal set frames the total sample space or logical universe.
Summary: Universal Set vs Null Set
The universal set contains all possible elements within a particular context, representing the complete collection under consideration, while the null set, or empty set, contains no elements at all, symbolizing the absence of any member. In set theory, the universal set is denoted by U and serves as the reference for defining subsets, whereas the null set is denoted by O and acts as the identity element for union operations. Understanding their relationship is fundamental to concepts such as complements, intersections, and unions in mathematics and logic.
Universal set Infographic
 libterm.com
libterm.com