Automorphism represents a fundamental concept in mathematics, describing a structure-preserving map from an object to itself, highlighting symmetries within algebraic structures like groups, rings, and graphs. Understanding automorphisms allows you to uncover intrinsic properties and invariants critical to various fields such as cryptography, geometry, and theoretical physics. Dive deeper into this article to explore how automorphisms shape mathematical theory and practical applications.
Table of Comparison
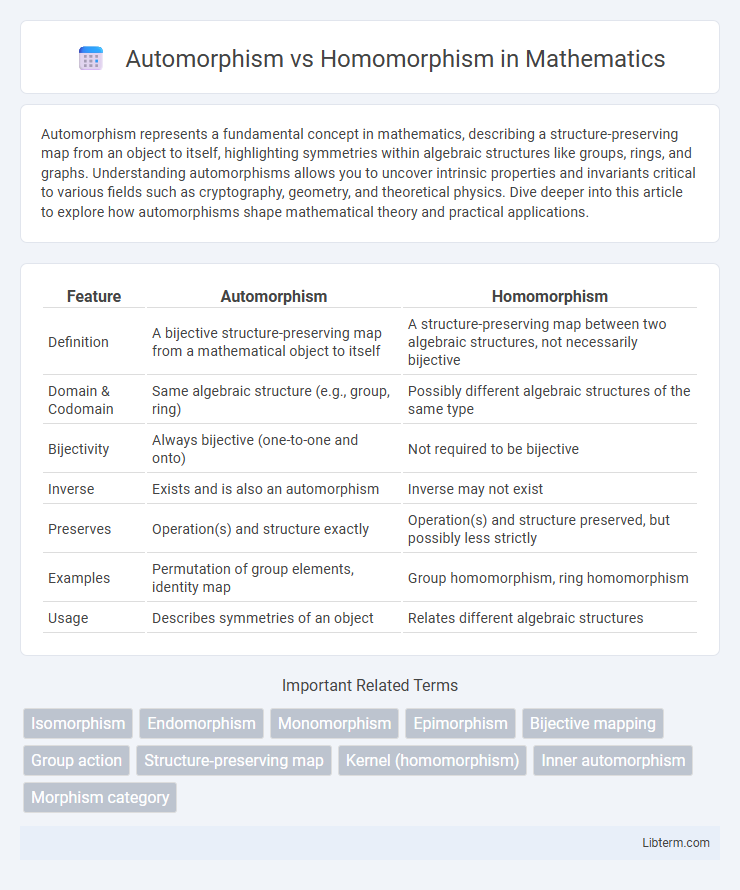
| Feature | Automorphism | Homomorphism |
|---|---|---|
| Definition | A bijective structure-preserving map from a mathematical object to itself | A structure-preserving map between two algebraic structures, not necessarily bijective |
| Domain & Codomain | Same algebraic structure (e.g., group, ring) | Possibly different algebraic structures of the same type |
| Bijectivity | Always bijective (one-to-one and onto) | Not required to be bijective |
| Inverse | Exists and is also an automorphism | Inverse may not exist |
| Preserves | Operation(s) and structure exactly | Operation(s) and structure preserved, but possibly less strictly |
| Examples | Permutation of group elements, identity map | Group homomorphism, ring homomorphism |
| Usage | Describes symmetries of an object | Relates different algebraic structures |
Introduction to Automorphism and Homomorphism
Automorphisms are structure-preserving isomorphisms from a mathematical object to itself, highlighting symmetries within the object. Homomorphisms are mappings between two algebraic structures that preserve operations such as addition or multiplication, enabling the study of structure relationships. Understanding automorphisms and homomorphisms is fundamental in fields like group theory, ring theory, and linear algebra for analyzing algebraic systems and their transformations.
Definitions: Automorphism Explained
An automorphism is a bijective homomorphism from a mathematical structure to itself that preserves all operations and relations intrinsic to the structure. It acts as an isomorphism within the same structure, ensuring the object's internal symmetry by mapping elements while maintaining algebraic properties. Automorphisms play a crucial role in group theory, ring theory, and other algebraic systems by describing the structure's self-similar transformations.
What is a Homomorphism?
A homomorphism is a structure-preserving map between two algebraic structures, such as groups, rings, or vector spaces, that respects the operations defined on those structures. It ensures that the image of an operation applied to elements equals the operation applied to the images of those elements, maintaining algebraic properties. Unlike automorphisms, which are bijective homomorphisms mapping a structure onto itself, homomorphisms may not be invertible or onto.
Core Differences Between Automorphism and Homomorphism
Automorphisms are bijective homomorphisms from an algebraic structure to itself, preserving both structure and invertibility, while homomorphisms are general structure-preserving maps that may not be bijective. The core difference lies in automorphisms being isomorphisms of a structure onto itself, ensuring a one-to-one correspondence, whereas homomorphisms allow for mappings between different structures without guaranteeing invertibility. This fundamental distinction affects properties such as kernel triviality and image coverage within groups, rings, or fields.
Key Properties of Automorphisms
Automorphisms are bijective homomorphisms from a mathematical structure to itself, preserving all structural properties without loss of information, making them isomorphisms of the structure with itself. Key properties include invertibility, preservation of operations (such as addition or multiplication in groups or rings), and maintenance of identity elements, ensuring structural symmetry and internal consistency. Unlike general homomorphisms, automorphisms also require the mapping to be surjective and injective, reflecting a perfect structural equivalence.
Fundamental Properties of Homomorphisms
Homomorphisms are structure-preserving maps between algebraic systems that maintain operation compatibility, ensuring the image of a product equals the product of the images. Core properties include kernel characterization, where the kernel forms a normal subgroup or ideal, and the image being a substructure that reflects the homomorphic image. Automorphisms are bijective homomorphisms from a structure onto itself, preserving all structural properties and forming the automorphism group.
Examples in Algebraic Structures
Automorphisms in algebraic structures are isomorphisms from an object to itself, such as the map \( f: \mathbb{Z} \to \mathbb{Z} \) defined by \( f(x) = -x \) in the group of integers under addition, which preserves group operations and is bijective. Homomorphisms are structure-preserving maps between different algebraic structures, like the ring homomorphism \( f: \mathbb{Z} \to \mathbb{Z}/n\mathbb{Z} \) given by \( f(x) = x \mod n \), which respects both addition and multiplication but may not be bijective. In vector spaces, an automorphism example is a linear transformation with an invertible matrix, while a homomorphism can be any linear map between spaces that may fail to be invertible.
Applications in Mathematics and Computer Science
Automorphisms serve as key tools in group theory and abstract algebra by providing insights into the symmetrical structure of algebraic objects, enabling classification and invariant analysis. Homomorphisms underpin the design of cryptographic algorithms and data structure transformations by preserving algebraic operations across different systems, facilitating secure communication protocols and efficient computation. Both concepts critically contribute to formal language theory and coding theory, optimizing pattern recognition and error correction methods in computer science.
Significance in Group Theory
Automorphisms in group theory are isomorphisms from a group to itself, preserving the group's structure and revealing its internal symmetries, crucial for understanding group invariants and classification. Homomorphisms, as structure-preserving maps between different groups, facilitate the study of group relationships and quotient structures, enabling the construction of new groups and analysis of group actions. The distinction highlights the importance of automorphisms in characterizing a group's self-symmetry, while homomorphisms serve as fundamental tools for exploring connections across different groups.
Summary: Choosing Between Automorphism and Homomorphism
Automorphisms are isomorphisms from a mathematical structure to itself, preserving all operations and reflecting structural symmetry, while homomorphisms are more general structure-preserving maps between different algebraic objects. Choose an automorphism when analyzing internal symmetries or when an invertible, structure-preserving transformation of a single object is required. Opt for a homomorphism to study relationships between different structures or to map elements while maintaining operation consistency without necessarily requiring invertibility.
Automorphism Infographic
 libterm.com
libterm.com