Borel sets form the foundation of measurable spaces in mathematics, constructed from open sets through countable unions, intersections, and complements. Understanding Borel sets is essential for analyzing functions, probability measures, and real analysis. Discover how Borel sets play a crucial role in your mathematical journey by exploring the details in the rest of this article.
Table of Comparison
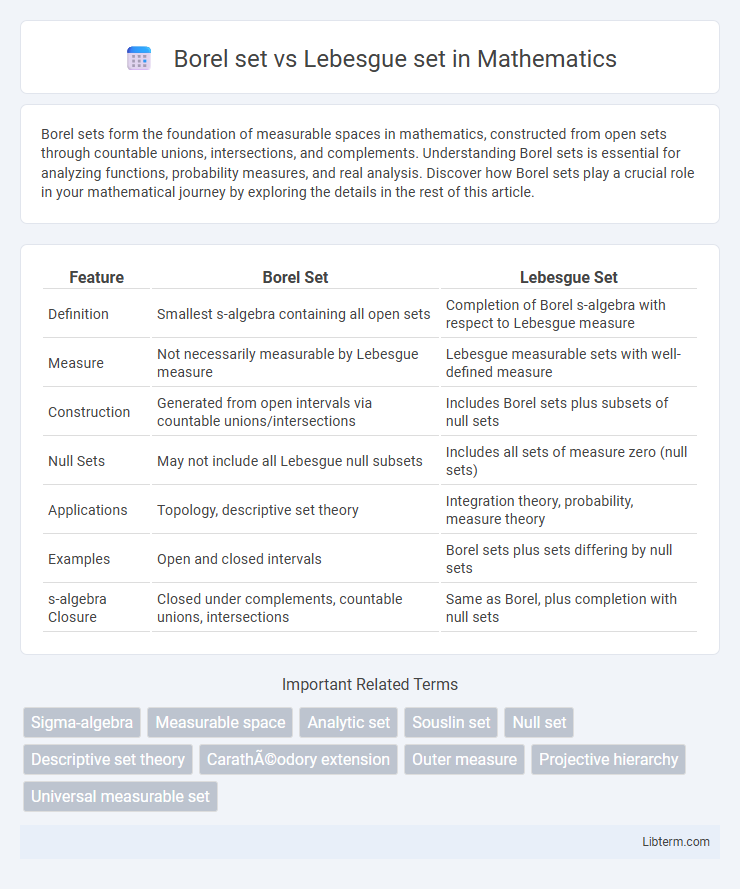
| Feature | Borel Set | Lebesgue Set |
|---|---|---|
| Definition | Smallest s-algebra containing all open sets | Completion of Borel s-algebra with respect to Lebesgue measure |
| Measure | Not necessarily measurable by Lebesgue measure | Lebesgue measurable sets with well-defined measure |
| Construction | Generated from open intervals via countable unions/intersections | Includes Borel sets plus subsets of null sets |
| Null Sets | May not include all Lebesgue null subsets | Includes all sets of measure zero (null sets) |
| Applications | Topology, descriptive set theory | Integration theory, probability, measure theory |
| Examples | Open and closed intervals | Borel sets plus sets differing by null sets |
| s-algebra Closure | Closed under complements, countable unions, intersections | Same as Borel, plus completion with null sets |
Introduction to Borel Sets and Lebesgue Sets
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the Borel sigma-algebra fundamental in topology and measure theory. Lebesgue sets extend Borel sets by including sets that differ from Borel sets by null sets, enabling a more comprehensive approach to measure theory with the Lebesgue measure. This distinction allows Lebesgue sets to measure more complex subsets of real numbers, crucial for advanced integration and probability theories.
Historical Development of Borel and Lebesgue Sets
The historical development of Borel sets began with Emile Borel in 1898, who introduced these sets as the smallest s-algebra containing all open intervals on the real line, forming a foundation for measure theory. Henri Lebesgue expanded this framework in the early 20th century by defining Lebesgue measurable sets, which include all Borel sets plus additional sets to create a complete measure space accommodating more functions for integration. This progression from Borel to Lebesgue sets allowed mathematicians to rigorously extend the notion of length and integrate a wider class of functions, revolutionizing modern analysis.
Defining Borel Sets: Properties and Construction
Borel sets are generated from open intervals through countable unions, intersections, and complements, forming the smallest s-algebra containing all open sets in a given topological space, typically the real line. These sets are crucial in measure theory as they provide the foundation for defining measures, including the Lebesgue measure, by capturing all measurable sets constructed via standard topological operations. Their properties include closure under countable set operations, enabling rigorous analysis and integration of functions over real numbers.
Understanding Lebesgue Sets: Definition and Characteristics
Lebesgue sets extend Borel sets by including all subsets of the real line that can be measured using Lebesgue measure, capturing more complex and irregularly shaped sets than Borel sets. These sets form a s-algebra generated by augmenting Borel sets with all null sets, allowing for a complete measure space in real analysis. Lebesgue sets are critical for integration theory, enabling the measurement of sets that Borel structures alone cannot handle, and are foundational to modern probability and functional analysis.
Hierarchy and Relationship: Borel Sets within Lebesgue Sets
Borel sets form the smallest s-algebra containing all open sets on the real line, serving as the foundation of measurable sets in classical topology. Lebesgue sets extend Borel sets by including all subsets of Borel sets that differ by a null set, thus creating a complete s-algebra essential for Lebesgue measure theory. This hierarchy establishes Borel sets as a subset of Lebesgue sets, highlighting the Lebesgue s-algebra's completeness and ability to measure more complex sets beyond the Borel framework.
Measurability: Borel Measurable vs. Lebesgue Measurable
Borel measurable sets form the smallest s-algebra generated by open intervals in the real line, ensuring measurability with respect to standard topological structures. Lebesgue measurable sets extend Borel sets by including all subsets differing from a Borel set by a null measure set, thus creating a more comprehensive s-algebra suitable for integration and measure theory. Lebesgue measurability captures a wider class of subsets essential for advanced analysis, particularly in handling limits and completeness not guaranteed by Borel measurability alone.
Examples: Classic Illustrations of Each Set
Borel sets include all open and closed intervals in the real line, such as the set of all rationals or unions of open intervals like (0,1) (2,3), which are generated from countable operations on open sets. Lebesgue measurable sets encompass all Borel sets plus sets created by adding or removing null sets, exemplified by Vitali sets modified to include specific measure-zero subsets. Classic examples of Borel sets are intervals and countable unions of intervals, while Lebesgue measurable sets extend these to more complex sets like those formed through measure completion involving null sets.
Applications in Measure Theory
Borel sets, generated from open intervals through countable unions and intersections, form the foundational sigma-algebra for defining Borel measures, essential in classical measure theory applications such as probability and topology. Lebesgue sets extend Borel sets by including all sets measurable with respect to Lebesgue measure, allowing for a more comprehensive treatment of functions and integrals particularly in real analysis and PDEs. The distinction enables advanced measure-theoretic techniques for handling discontinuities and irregular sets, crucial for accurate integration and functional analysis.
Common Misconceptions and Pitfalls
Borel sets are generated from open intervals through countable unions, intersections, and complements, whereas Lebesgue sets form a s-algebra that extends Borel sets to include all subsets measurable with respect to Lebesgue measure. A common misconception is assuming all subsets of real numbers are Lebesgue measurable, while in reality, there exist non-measurable sets beyond both Borel and Lebesgue frameworks. Another pitfall involves conflating Borel measurability with Lebesgue measurability, neglecting that Lebesgue measurable sets include limit operations involving null sets, making them strictly more comprehensive than Borel sets.
Conclusion: Comparing Borel and Lebesgue Sets
Borel sets form the smallest s-algebra containing all open sets in a given topological space, primarily used in measure theory for defining Borel measures. Lebesgue sets extend Borel sets by including all subsets of null sets, enabling a complete measure that assigns zero to negligible sets and resolves limitations of Borel measures regarding measure completion. The Lebesgue s-algebra is strictly larger than the Borel s-algebra, providing a more comprehensive framework for integration and probability theory by including all sets necessary for a complete measure.
Borel set Infographic
 libterm.com
libterm.com