Laurent series extend the concept of Taylor series by allowing terms with negative powers, providing a powerful tool for representing complex functions near singularities. This series is essential in complex analysis for classifying and understanding the behavior of functions around isolated singular points. Explore the full article to discover how Laurent series can deepen your understanding of complex functions and their applications.
Table of Comparison
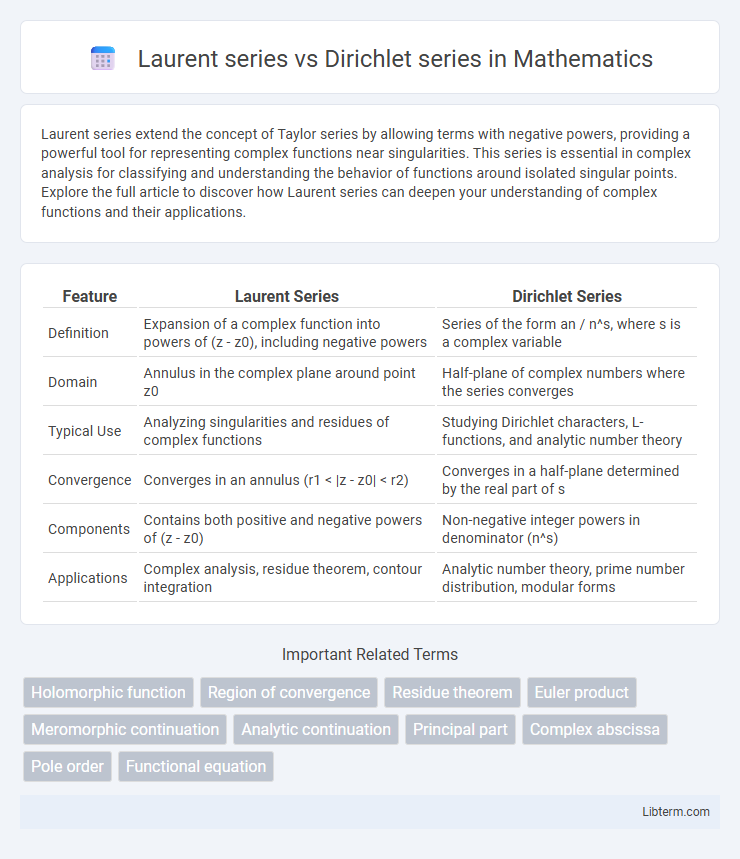
| Feature | Laurent Series | Dirichlet Series |
|---|---|---|
| Definition | Expansion of a complex function into powers of (z - z0), including negative powers | Series of the form an / n^s, where s is a complex variable |
| Domain | Annulus in the complex plane around point z0 | Half-plane of complex numbers where the series converges |
| Typical Use | Analyzing singularities and residues of complex functions | Studying Dirichlet characters, L-functions, and analytic number theory |
| Convergence | Converges in an annulus (r1 < |z - z0| < r2) | Converges in a half-plane determined by the real part of s |
| Components | Contains both positive and negative powers of (z - z0) | Non-negative integer powers in denominator (n^s) |
| Applications | Complex analysis, residue theorem, contour integration | Analytic number theory, prime number distribution, modular forms |
Introduction to Laurent Series and Dirichlet Series
Laurent series represent complex functions as infinite sums including terms with both positive and negative powers of (z - z0), crucial for analyzing singularities in complex analysis. Dirichlet series are infinite sums of the form a_n / n^s, where s is a complex variable and a_n are coefficients, commonly used in number theory to study arithmetic functions and L-functions. Both series serve distinct purposes: Laurent series provide local expansions near singular points, while Dirichlet series encode number-theoretic properties through analytic continuation and convergence in specific half-planes.
Historical Background and Development
The Laurent series, introduced by Pierre Alphonse Laurent in the 19th century, expanded the toolkit for complex analysis by generalizing power series to include negative powers, enabling the study of functions with singularities. Dirichlet series, named after Johann Peter Gustav Lejeune Dirichlet, originated in the context of number theory in the mid-19th century and are instrumental in the analytic study of arithmetic functions through infinite series of the form \(\sum a_n n^{-s}\). Both series have evolved through rigorous mathematical research, with Laurent series becoming foundational in complex function theory and Dirichlet series playing a crucial role in analytic number theory and the distribution of primes.
Mathematical Definitions and Formalisms
Laurent series represent complex functions as infinite sums including terms with negative powers, formalized as \( f(z) = \sum_{n=-\infty}^{\infty} a_n (z - c)^n \) where \( z \) is a complex variable and \( c \) is the center of expansion. Dirichlet series are expressed as infinite sums of the form \( D(s) = \sum_{n=1}^{\infty} \frac{a_n}{n^s} \), where \( s \) is a complex variable and the coefficients \( a_n \) often encode arithmetic or analytic properties. While Laurent series focus on local behavior near singularities in the complex plane, Dirichlet series are primarily used in analytic number theory to study distributions of arithmetic functions through complex analytic methods.
Convergence Criteria: Laurent vs Dirichlet Series
Laurent series converge in annular regions defined by inner and outer radii where the series coefficients decay suitably, relying on the distance from singularities for convergence. Dirichlet series converge in half-planes of the complex plane, determined by the abscissa of convergence, where the real part of the complex variable exceeds a critical threshold linked to the growth rate of the series coefficients. The key difference lies in geometric regions: Laurent series convergence depends on radial bounds around singularities, while Dirichlet series convergence is governed by vertical strips or half-planes characterized by the abscissa of absolute or uniform convergence.
Domain of Application and Use Cases
Laurent series are predominantly used in complex analysis to represent functions with isolated singularities, making them essential for solving problems involving residues and contour integration. Dirichlet series find primary application in analytic number theory, particularly in studying the distribution of prime numbers through functions like the Riemann zeta function. While Laurent series apply to complex functions defined in annular regions, Dirichlet series converge in half-planes of the complex plane, enabling analysis of arithmetic functions and L-series.
Analytical Properties and Representation
Laurent series, expressed as a power series with both positive and negative integer exponents, provide analytic representations of complex functions within annular regions, capturing singularities through principal parts. Dirichlet series, typically infinite sums of the form \(\sum_{n=1}^\infty a_n n^{-s}\), represent functions analytic in half-planes and are central in number theory, particularly for encoding arithmetic information via their coefficients. While Laurent series localize singular behavior in the complex plane around isolated points, Dirichlet series exhibit global analytic properties related to complex variables \(s\), with meromorphic continuations and functional equations reflecting deep arithmetic structure.
Relationship with Other Series (e.g., Taylor, Fourier)
Laurent series generalize Taylor series by including negative powers, enabling the representation of functions with singularities, while Dirichlet series express functions as infinite sums involving terms like n^(-s), commonly used in number theory. Laurent series share a close relationship with Fourier series since both decompose functions into sums of powers or exponentials, facilitating analysis in complex and periodic domains respectively. Dirichlet series connect to generating functions and zeta functions, linking analytic number theory with series expansions, but unlike Laurent and Fourier series, they do not directly expand around points or frequencies.
Examples Illustrating Key Differences
Laurent series, such as \( f(z) = \sum_{n=-\infty}^{\infty} a_n (z - z_0)^n \), illustrate their use in complex analysis by representing functions with isolated singularities using both positive and negative powers of \((z - z_0)\). Dirichlet series, exemplified by the Riemann zeta function \(\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} \), focus on infinite sums indexed by natural numbers raised to a complex power, central to analytic number theory. The key difference lies in Laurent series' domain over complex variables with local expansions around singularities, whereas Dirichlet series depend on a complex parameter within a half-plane and analyze distribution properties of arithmetic functions.
Advantages and Limitations of Each Series
Laurent series excel in representing complex functions with singularities by incorporating both positive and negative powers of (z - z0), enabling precise analysis near poles and essential singularities but are restricted to functions holomorphic in annular regions. Dirichlet series, typically expressed as a sum over n^(-s), are fundamental in number theory and analytic continuation of functions like the Riemann zeta function, offering powerful tools for studying distribution of prime numbers, yet they face convergence limitations confined to half-planes and lack direct applicability to isolated singularities. While Laurent series provide local expansions around singular points beneficial for residue computations, Dirichlet series serve best for global properties of arithmetic functions, illustrating complementary strengths in complex analysis and number theory contexts.
Conclusion and Further Reading
Laurent series expand complex functions into powers of (z - z0), capturing singularities through negative exponents, while Dirichlet series represent functions as infinite sums indexed by natural numbers with general term an/ns, primarily used in analytic number theory. Understanding these series highlights their distinct applications: Laurent series underpin complex analysis and residue theory, whereas Dirichlet series facilitate studying multiplicative functions and prime distributions. For deeper insights, consult texts like "Complex Analysis" by Lars Ahlfors for Laurent series and "Multiplicative Number Theory" by Harold Davenport for Dirichlet series.
Laurent series Infographic
 libterm.com
libterm.com