Mastering the fundamentals of your chosen field is essential for building expertise and driving innovation. Staying updated with the latest trends and technologies ensures you remain competitive and relevant in a rapidly evolving industry. Discover how you can elevate your skills and make a significant impact by reading the rest of the article.
Table of Comparison
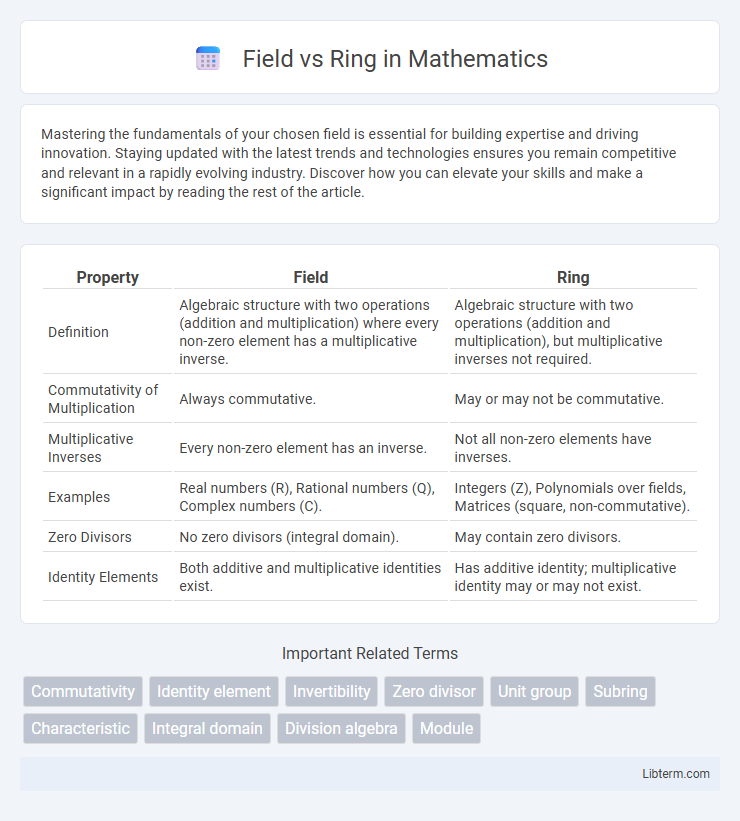
| Property | Field | Ring |
|---|---|---|
| Definition | Algebraic structure with two operations (addition and multiplication) where every non-zero element has a multiplicative inverse. | Algebraic structure with two operations (addition and multiplication), but multiplicative inverses not required. |
| Commutativity of Multiplication | Always commutative. | May or may not be commutative. |
| Multiplicative Inverses | Every non-zero element has an inverse. | Not all non-zero elements have inverses. |
| Examples | Real numbers (R), Rational numbers (Q), Complex numbers (C). | Integers (Z), Polynomials over fields, Matrices (square, non-commutative). |
| Zero Divisors | No zero divisors (integral domain). | May contain zero divisors. |
| Identity Elements | Both additive and multiplicative identities exist. | Has additive identity; multiplicative identity may or may not exist. |
Introduction to Field and Ring
A field is an algebraic structure consisting of a set equipped with two operations, addition and multiplication, where every nonzero element has a multiplicative inverse, ensuring division is always possible. In contrast, a ring also consists of a set with two operations but does not require every nonzero element to have a multiplicative inverse, allowing for the presence of zero divisors. Fields play a fundamental role in algebra due to their stricter properties, enabling more comprehensive arithmetic operations compared to rings.
Fundamental Definitions
A field is a set equipped with two operations, addition and multiplication, where every non-zero element has a multiplicative inverse, making division always possible except by zero. A ring is a set with two operations, addition and multiplication, where addition forms an abelian group, multiplication is associative, but multiplicative inverses do not necessarily exist for all non-zero elements. The key distinction lies in the presence of multiplicative inverses for every non-zero element in fields, contrasting with rings where inverses may be absent, defining their fundamental algebraic structures.
Key Differences between Field and Ring
A field is a commutative ring with unity where every nonzero element has a multiplicative inverse, enabling division without zero denominators, while a ring may lack multiplicative inverses for some elements and does not require commutativity. Fields guarantee the existence of multiplicative inverses and commutativity of multiplication, critical for solving linear equations and algebraic structures such as vector spaces. Rings only ensure associative addition and multiplication, distributive laws, and may include zero divisors, making them broader algebraic systems without the restrictive properties found in fields.
Structure and Properties of Rings
Rings are algebraic structures consisting of a set equipped with two binary operations: addition and multiplication, where addition forms an abelian group and multiplication is associative but not necessarily commutative or invertible. Unlike fields, rings do not require every nonzero element to have a multiplicative inverse, allowing the existence of zero divisors and non-invertible elements, which leads to diverse examples such as polynomial rings and matrix rings. The structural differences impact properties like divisibility, ideal formation, and factorization, making rings a broader class with applications ranging from number theory to abstract algebra and functional analysis.
Structure and Properties of Fields
Fields are algebraic structures characterized by two operations, addition and multiplication, where every nonzero element possesses a multiplicative inverse, ensuring division is always possible. Unlike rings, fields are commutative with respect to multiplication and contain no zero divisors, guaranteeing unique factorization and a well-defined division algorithm. These properties enable fields to serve as foundational constructs in linear algebra, number theory, and algebraic geometry.
Examples of Rings and Fields
Fields include structures like the rational numbers (Q), real numbers (R), and complex numbers (C), where every non-zero element has a multiplicative inverse. Rings encompass a broader class of algebraic systems such as the integers (Z), polynomial rings (R[x]), and matrix rings (M_n(R)), which may lack multiplicative inverses for some elements. Understanding examples like finite fields (GF(p)) and integral domains (subclass of rings) clarifies the distinctive properties and applications of fields and rings in algebra.
Arithmetic Operations in Rings vs Fields
In fields, every nonzero element has a multiplicative inverse, enabling division operations without restrictions, which allows for more comprehensive arithmetic manipulations compared to rings. Rings may lack multiplicative inverses for some nonzero elements, restricting division and causing some arithmetic operations to be undefined. This fundamental difference impacts the complexity of algebraic structures and the solvability of equations within rings versus fields.
Applications in Mathematics and Science
Fields provide a robust algebraic structure with commutative multiplication and multiplicative inverses for all nonzero elements, making them essential in solving polynomial equations and in the development of linear algebra. Rings, allowing addition and multiplication without the necessity of multiplicative inverses, play a crucial role in number theory, algebraic geometry, and cryptography, particularly in the study of integer properties and modular arithmetic systems. Applications in physics and chemistry often leverage fields for vector space formulations, while rings underpin the algebraic frameworks for coding theory and error detection algorithms.
Importance in Abstract Algebra
Fields and rings are fundamental algebraic structures in abstract algebra, with fields providing a richer framework due to the existence of multiplicative inverses for all nonzero elements, enabling division operations. Rings, while more general and less restrictive, are essential for studying structures where division is not always possible, such as in integers and polynomial rings. The distinction between fields and rings is crucial for understanding concepts like factorization, algebraic extensions, and advanced topics in number theory and geometry.
Summary: Choosing between Field and Ring
Fields provide a structure where division is always possible except by zero, making them ideal for algebraic systems requiring inverses, such as vector spaces and rational number arithmetic. Rings relax this requirement by allowing multiplication without every element having an inverse, suited for integer arithmetic and polynomial coefficient sets. Choosing between a field and a ring depends on the necessity of multiplicative inverses; if inverses are essential, a field is appropriate, whereas rings accommodate broader algebraic applications with potentially more complex factorization properties.
Field Infographic
 libterm.com
libterm.com