Homeomorphism is a fundamental concept in topology describing a continuous, bijective function with a continuous inverse between two topological spaces, indicating they are topologically equivalent. This mathematical transformation preserves properties like connectedness and compactness, allowing one to study spaces under deformation without tearing or gluing. Explore the rest of the article to understand how homeomorphisms shape modern geometric and topological analysis.
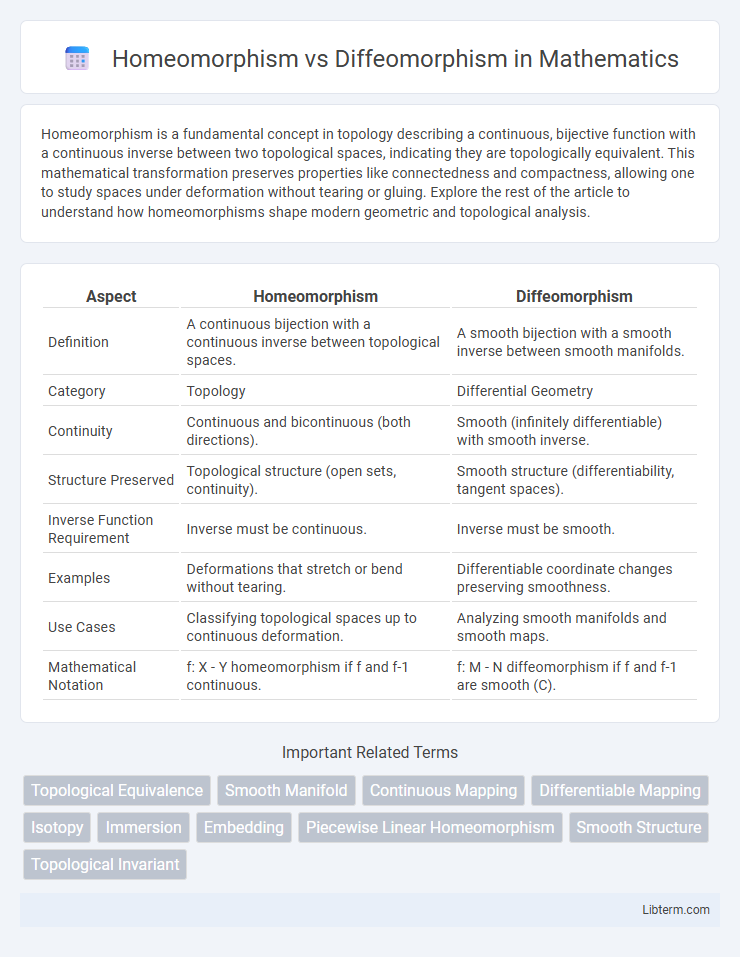
Table of Comparison
| Aspect | Homeomorphism | Diffeomorphism |
|---|---|---|
| Definition | A continuous bijection with a continuous inverse between topological spaces. | A smooth bijection with a smooth inverse between smooth manifolds. |
| Category | Topology | Differential Geometry |
| Continuity | Continuous and bicontinuous (both directions). | Smooth (infinitely differentiable) with smooth inverse. |
| Structure Preserved | Topological structure (open sets, continuity). | Smooth structure (differentiability, tangent spaces). |
| Inverse Function Requirement | Inverse must be continuous. | Inverse must be smooth. |
| Examples | Deformations that stretch or bend without tearing. | Differentiable coordinate changes preserving smoothness. |
| Use Cases | Classifying topological spaces up to continuous deformation. | Analyzing smooth manifolds and smooth maps. |
| Mathematical Notation | f: X - Y homeomorphism if f and f-1 continuous. | f: M - N diffeomorphism if f and f-1 are smooth (C). |
Introduction to Homeomorphism and Diffeomorphism
Homeomorphism is a continuous bijection between topological spaces with a continuous inverse, preserving topological properties such as connectedness and compactness. Diffeomorphism strengthens this concept within smooth manifolds by requiring both the map and its inverse to be smooth, ensuring preservation of differentiable structures. These concepts are fundamental in topology and differential geometry for classifying spaces based on their structural properties rather than mere shape.
Fundamental Concepts in Topology and Smooth Manifolds
Homeomorphisms are continuous, bijective functions with continuous inverses that preserve topological properties, enabling deformation of spaces without tearing or gluing. Diffeomorphisms extend this concept to smooth manifolds by requiring differentiability with smooth inverses, preserving the manifold's smooth structure. Understanding these distinctions is crucial for analyzing equivalences in topology and differential geometry.
Defining Homeomorphisms: Basics and Examples
Homeomorphisms are continuous functions between topological spaces that have continuous inverses, preserving the topological structure without tearing or gluing. Examples include the deformation of a coffee cup into a donut shape, illustrating their fundamental role in topology. Unlike diffeomorphisms, homeomorphisms do not require differentiability, focusing solely on topological equivalence.
Understanding Diffeomorphisms: Key Properties
Diffeomorphisms are smooth bijections between manifolds with smooth inverses, preserving differentiable structures and enabling advanced analysis in differential geometry. They ensure the transfer of geometric and analytic properties, maintaining smoothness and local Euclidean behavior. Unlike homeomorphisms, which preserve topological properties without requiring smoothness, diffeomorphisms guarantee the compatibility of calculus on manifolds, crucial for studies in smooth manifolds and dynamical systems.
Core Differences Between Homeomorphism and Diffeomorphism
Homeomorphisms are continuous bijections with continuous inverses between topological spaces, preserving topological properties but not necessarily smooth structures. Diffeomorphisms are bijections between smooth manifolds that are differentiable with differentiable inverses, preserving smooth structure and allowing for calculus-based analysis. The core difference lies in smoothness requirements: homeomorphisms maintain topology while diffeomorphisms preserve both topology and differentiable structures.
Mathematical Significance in Topology and Geometry
Homeomorphism represents a continuous, bijective mapping with a continuous inverse, preserving topological properties such as connectedness and compactness, thus classifying spaces up to topological equivalence. Diffeomorphism extends this concept to smooth manifolds by requiring differentiability and smooth invertibility, preserving geometric structures like tangent spaces and enabling the study of smooth structures and curvature. The distinction highlights the interplay between topology, concerned with qualitative properties, and differential geometry, focused on smoothness and metric properties.
Examples Illustrating Homeomorphic but not Diffeomorphic Spaces
A classic example illustrating spaces that are homeomorphic but not diffeomorphic involves the topological sphere \(S^2\) and an exotic sphere, which are homeomorphic as topological manifolds but differ in their smooth structures. Another example is the quotient space formed by identifying antipodal points on a sphere, resulting in a projective plane that is homeomorphic to a standard manifold but lacks a differentiable structure compatible with the original sphere. These examples highlight the subtle distinction between continuous bijections with continuous inverses (homeomorphisms) and smooth bijections with smooth inverses (diffeomorphisms) in differential topology.
Applications in Mathematics and Physics
Homeomorphisms classify topological spaces by preserving properties such as continuity and connectedness, playing a crucial role in topology and the study of manifold structures. Diffeomorphisms refine this classification by preserving smooth structures, enabling their use in differential geometry, general relativity, and fluid dynamics for modeling smooth deformations and coordinate changes. Applications in physics include characterizing phase spaces in Hamiltonian mechanics and studying spacetime manifolds under smooth transformations.
Key Theorems and Counterexamples
Key theorems in topology establish that every diffeomorphism is a homeomorphism, but the converse is not necessarily true, highlighting the distinction between smooth and continuous structures. The Whitney Embedding Theorem guarantees smooth manifolds can be embedded in Euclidean space, emphasizing the role of diffeomorphisms in smooth manifold classification. Counterexamples such as exotic spheres demonstrate manifolds that are homeomorphic but not diffeomorphic, illustrating the nuanced relationship between topological and smooth equivalences.
Conclusion: Choosing Between Homeomorphism and Diffeomorphism
Choosing between homeomorphism and diffeomorphism depends on the context of topological versus smooth structure preservation. Homeomorphisms maintain topological equivalences, making them ideal for general continuity and shape-related problems, while diffeomorphisms require differentiability, essential in differential geometry and smooth manifold theory. Selecting the appropriate concept ensures precise application in fields like topology, geometry, and mathematical physics.
Homeomorphism Infographic
 libterm.com
libterm.com