Topological spaces form the foundational framework for studying continuity, convergence, and boundary properties in mathematics, defined by a set equipped with a collection of open sets satisfying specific axioms. Understanding these spaces enables you to explore complex concepts such as compactness, connectedness, and metric spaces, which are crucial across various mathematical and applied disciplines. Discover more about topological spaces and their significance in the following article.
Table of Comparison
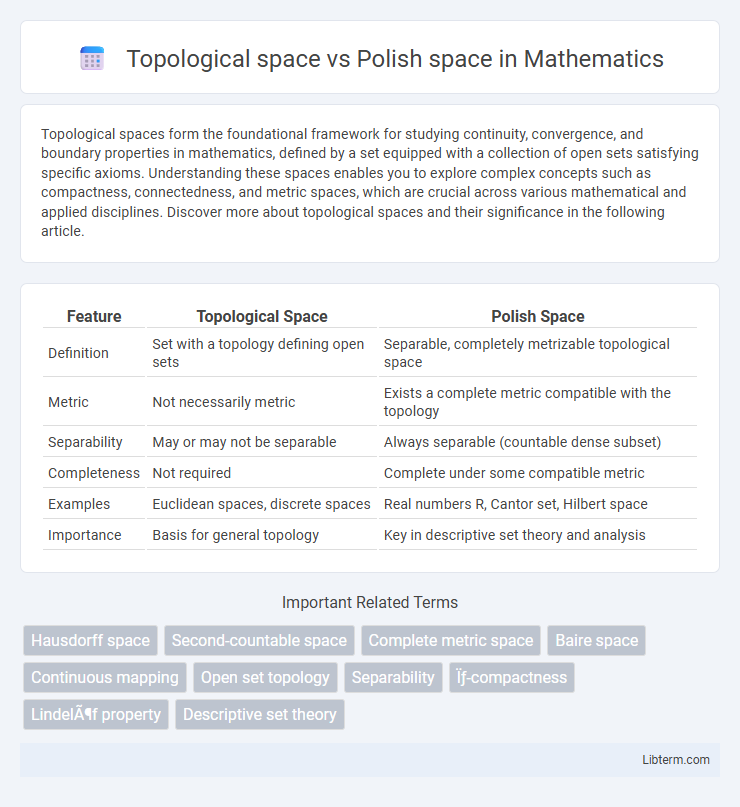
| Feature | Topological Space | Polish Space |
|---|---|---|
| Definition | Set with a topology defining open sets | Separable, completely metrizable topological space |
| Metric | Not necessarily metric | Exists a complete metric compatible with the topology |
| Separability | May or may not be separable | Always separable (countable dense subset) |
| Completeness | Not required | Complete under some compatible metric |
| Examples | Euclidean spaces, discrete spaces | Real numbers R, Cantor set, Hilbert space |
| Importance | Basis for general topology | Key in descriptive set theory and analysis |
Introduction to Topological and Polish Spaces
Topological spaces provide a fundamental framework in mathematics by defining a set equipped with a topology, which specifies how subsets relate as open or closed, enabling the study of continuity, convergence, and connectedness. Polish spaces, a special class of topological spaces, are separable completely metrizable spaces that play a crucial role in descriptive set theory and analysis due to their rich structure and well-behaved properties. Understanding the distinction between general topological spaces and Polish spaces involves grasping the importance of metrics, completeness, separability, and the implications these properties have on function spaces and measure theory.
Definition of Topological Space
A topological space is defined as a set equipped with a collection of open subsets that satisfy the axioms of union, finite intersection, and inclusion of the empty set and the entire set. Polish spaces are a special class of topological spaces that are separable and completely metrizable, meaning their topology arises from a complete metric inducing a countable dense subset. This distinction highlights that every Polish space is a topological space, but not all topological spaces meet the criteria to be considered Polish.
Key Properties of Topological Spaces
Topological spaces are defined by a set equipped with a collection of open sets satisfying axioms of union, finite intersection, and inclusion of the set and empty set, forming the foundational structure for continuity and convergence. Key properties include separation axioms (T0, T1, T2 or Hausdorff), compactness, connectedness, and metrizability, which determine how the space behaves under limits and mappings. While Polish spaces are a special class with complete separable metric structures, understanding topological spaces' properties is essential for analyzing more specialized spaces like Polish spaces.
Definition of Polish Space
A Polish space is a separable completely metrizable topological space, meaning it has a metric inducing its topology under which it is complete and contains a countable dense subset. Unlike general topological spaces, which may lack metrizability or separability, Polish spaces provide a rich structure for analysis due to their well-behaved metric properties. This completeness and separability facilitate significant applications in descriptive set theory, probability, and functional analysis.
Core Characteristics of Polish Spaces
Polish spaces are topological spaces that are separable and completely metrizable, meaning they admit a metric under which the space is complete and has a countable dense subset. Unlike general topological spaces, Polish spaces possess rich structure enabling the application of descriptive set theory and measure theory, making them essential in analysis and probability theory. Core characteristics include their compatibility with a complete metric, separability, and the presence of a countable basis, distinguishing them from broader classes of topological spaces.
Major Differences Between Topological and Polish Spaces
Topological spaces are general structures defined by open sets, providing the framework for continuity, convergence, and separation, while Polish spaces are a specialized class of topological spaces that are separable and completely metrizable. Unlike arbitrary topological spaces, Polish spaces possess a compatible metric that renders them complete, enabling powerful analytical tools such as Borel hierarchy and descriptive set theory applications. The key distinction lies in the added constraints of separability and complete metrizability, which endow Polish spaces with richer structure than general topological spaces.
Examples of Topological Spaces
Topological spaces include a broad variety of structures such as metric spaces, discrete spaces, and subspace topologies, providing a general framework for continuity and convergence. Polish spaces are a specialized class of topological spaces that are separable and completely metrizable, examples include the real numbers with the standard Euclidean topology and the Cantor set. Unlike general topological spaces that may lack metric properties, Polish spaces guarantee well-understood analytical properties essential in descriptive set theory and analysis.
Examples of Polish Spaces
Polish spaces, defined as separable completely metrizable topological spaces, include classic examples such as the real line \(\mathbb{R}\) with the standard topology, the Cantor set, and the Baire space \(\mathbb{N}^\mathbb{N}\) with the product topology. Unlike general topological spaces, Polish spaces possess a compatible metric that generates their topology, enabling advanced descriptive set theory and measure-theoretic applications. Other notable Polish spaces comprise Hilbert spaces like \(\ell^2\) and function spaces such as \(C([0,1])\) endowed with the uniform metric.
Importance and Applications in Mathematics
Topological spaces provide a fundamental framework for analyzing continuity, convergence, and boundary properties in various mathematical contexts, forming the basis for fields like algebraic topology and functional analysis. Polish spaces, being separable and completely metrizable topological spaces, are crucial in descriptive set theory, probability theory, and dynamical systems due to their rich structure and well-behaved measure-theoretic properties. The distinction allows mathematicians to leverage the generality of topological spaces while exploiting the analytic tractability and robustness of Polish spaces in complex mathematical modeling and classification problems.
Summary: Topological Space vs Polish Space
Topological spaces are general mathematical structures defined by open sets satisfying union and intersection properties, serving as the foundation for continuity and convergence. Polish spaces are a specific class of topological spaces that are separable and completely metrizable, meaning they possess a metric inducing the topology and a countable dense subset. The distinction lies in Polish spaces' additional constraints of separability and completeness, which make them central in descriptive set theory and analysis.
Topological space Infographic
 libterm.com
libterm.com