Infinitely complete systems offer limitless possibilities by continuously adapting and expanding their capabilities without constraints. These systems integrate advanced algorithms and data to ensure seamless performance across diverse applications. Explore the rest of the article to discover how infinite completeness can transform your approach and maximize efficiency.
Table of Comparison
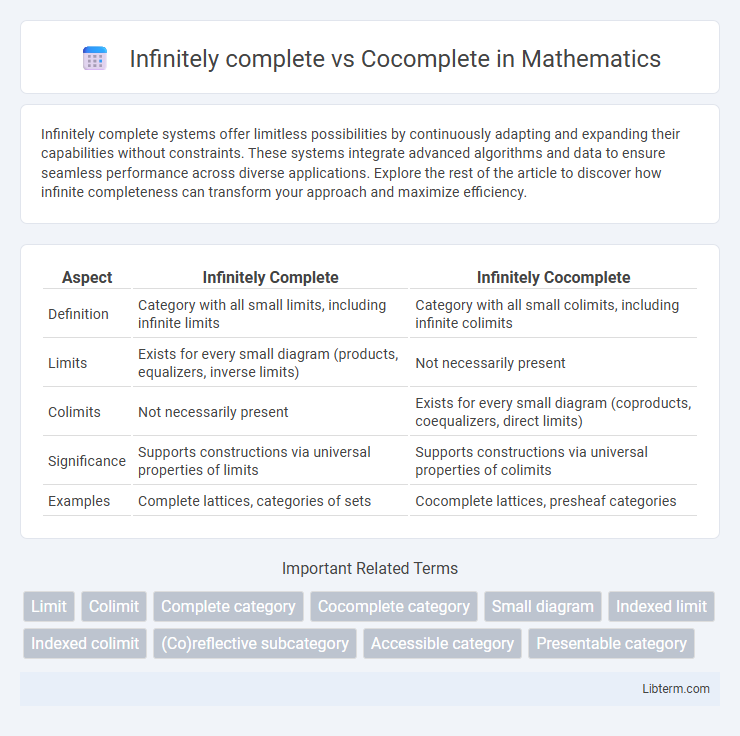
| Aspect | Infinitely Complete | Infinitely Cocomplete |
|---|---|---|
| Definition | Category with all small limits, including infinite limits | Category with all small colimits, including infinite colimits |
| Limits | Exists for every small diagram (products, equalizers, inverse limits) | Not necessarily present |
| Colimits | Not necessarily present | Exists for every small diagram (coproducts, coequalizers, direct limits) |
| Significance | Supports constructions via universal properties of limits | Supports constructions via universal properties of colimits |
| Examples | Complete lattices, categories of sets | Cocomplete lattices, presheaf categories |
Introduction to Completeness in Category Theory
Completeness in category theory refers to the existence of all small limits within a category, ensuring the ability to construct products, equalizers, and inverse limits. Cocontinuity, or cocompleteness, involves the existence of all small colimits, enabling the formation of coproducts, coequalizers, and direct limits. Infinitely complete categories have all small limits indexed by arbitrary sets, while cocomplete categories possess all small colimits, essential for various constructions and universal properties in advanced mathematical contexts.
Defining Infinitely Complete Categories
Infinitely complete categories are defined by the existence of all small limits, including products, equalizers, and inverse limits, which ensures the ability to construct objects by "completing" diagrams indexed by any small category. In contrast, cocomplete categories possess all small colimits, such as coproducts, coequalizers, and direct limits, enabling the formation of colimits indexed by small categories. The distinction highlights the dual nature of completeness in category theory, where infinite completeness ensures the preservation of limits crucial for constructions in topology and algebra.
Understanding Cocompleteness: The Basics
Cocompleteness in category theory refers to a category having all small colimits, meaning it supports the construction of all diagrams indexed by small categories through colimits like coproducts and coequalizers. Infinitely cocomplete categories extend this concept by possessing all colimits indexed by arbitrarily large diagrams, ensuring the existence of colimits for infinite constructions. Understanding cocompleteness is crucial for working with categories where the aggregation of morphisms and objects into colimits enables complex algebraic and topological structures.
Key Differences Between Infinitely Complete and Cocomplete Categories
Infinitely complete categories possess all small limits, including products, equalizers, and pullbacks, enabling the construction of universal cones over diagrams. In contrast, infinitely cocomplete categories have all small colimits such as coproducts, coequalizers, and pushouts, allowing the formation of universal co-cones. The key difference lies in the directional nature of these universal constructions: limits represent universal cones into a diagram, while colimits represent universal co-cones out of a diagram within category theory.
Importance of Limits in Infinitely Complete Categories
Infinitely complete categories possess all small limits, enabling the construction and manipulation of complex objects through products, equalizers, and pullbacks. Limits in these categories are crucial for defining universal properties, ensuring consistency, and facilitating the study of functors and natural transformations. This completeness empowers categorical frameworks to model intricate structures in algebra, topology, and logic, supporting advanced mathematical reasoning and applications.
Role of Colimits in Cocomplete Categories
Colimits in cocomplete categories serve as universal constructions that generalize the notion of unions, quotients, and direct limits, enabling the assembly of complex objects from diagrams of simpler ones. Infinitely complete categories possess all limits for arbitrary diagrams, which provide a dual perspective, but colimits specifically capture the process of coalescing information, reflecting essential features like coproducts and coequalizers. The existence of all small colimits in cocomplete categories is crucial for constructions in topology, algebraic geometry, and category theory, supporting the formation of pushouts, cofibers, and other critical categorical constructions.
Examples of Infinitely Complete Categories
Infinitely complete categories possess all small limits, such as products and equalizers, ensuring the existence of limits over any small diagram; a classic example is the category of sets (Set), which has all small limits including infinite products. Other examples include the category of complete lattices, where arbitrary meets (infima) exist, and the category of topological spaces (Top), which admits all limits formed via product and subspace constructions. These categories contrast with cocomplete ones, where all small colimits exist, such as coproducts and coequalizers, highlighting the dual nature in categorical completeness properties.
Typical Instances of Cocomplete Categories
Typical instances of cocomplete categories include the category of sets (Set), the category of vector spaces over a field (Vect_k), and the category of topological spaces (Top), all of which possess all small colimits. Infinitely complete categories, on the other hand, have all small limits, exemplified by categories such as complete lattices and complete metric spaces. Understanding cocompleteness is crucial for constructions like colimits, coproducts, and coequalizers, which are central to algebraic and topological frameworks.
Applications in Mathematics and Computer Science
Infinitely complete categories possess all small limits, enabling the construction of intricate mathematical objects and supporting advanced structures in algebraic topology and category theory, while cocomplete categories have all small colimits, facilitating the formation of quotients, coequalizers, and data aggregation processes crucial in programming language semantics and type theory. The interplay between infinite completeness and cocompleteness underpins the design of functional programming languages, where colimits model computations such as merging data streams and limits encode constraints or invariants in data types. The distinction shapes the development of categorical models in logic, database theory, and domain theory, optimizing data transformation and reasoning frameworks foundational to theoretical computer science.
Summary: Choosing Between Completeness and Cocompleteness
Infinitely complete categories possess all small limits, enabling the construction of universal cones over diagrams, while cocomplete categories have all small colimits, allowing the formation of co-cones. The choice between completeness and cocompleteness depends on the specific categorical constructions required: limits support operations like products and equalizers, whereas colimits facilitate coproducts and coequalizers. Understanding the interplay between these properties is essential for selecting the appropriate framework in fields such as algebraic topology, category theory, and algebraic geometry.
Infinitely complete Infographic
 libterm.com
libterm.com