The Poincare-Hopf theorem relates the indices of vector fields' singularities on a compact differentiable manifold to its Euler characteristic, providing a powerful tool in topology for understanding manifold structure. It ensures that the sum of the indices of isolated singular points equals the Euler characteristic of the manifold, linking local vector field behavior to global topological invariants. Discover how this theorem unlocks deeper insights into differential topology by exploring its applications and proofs in the rest of the article.
Table of Comparison
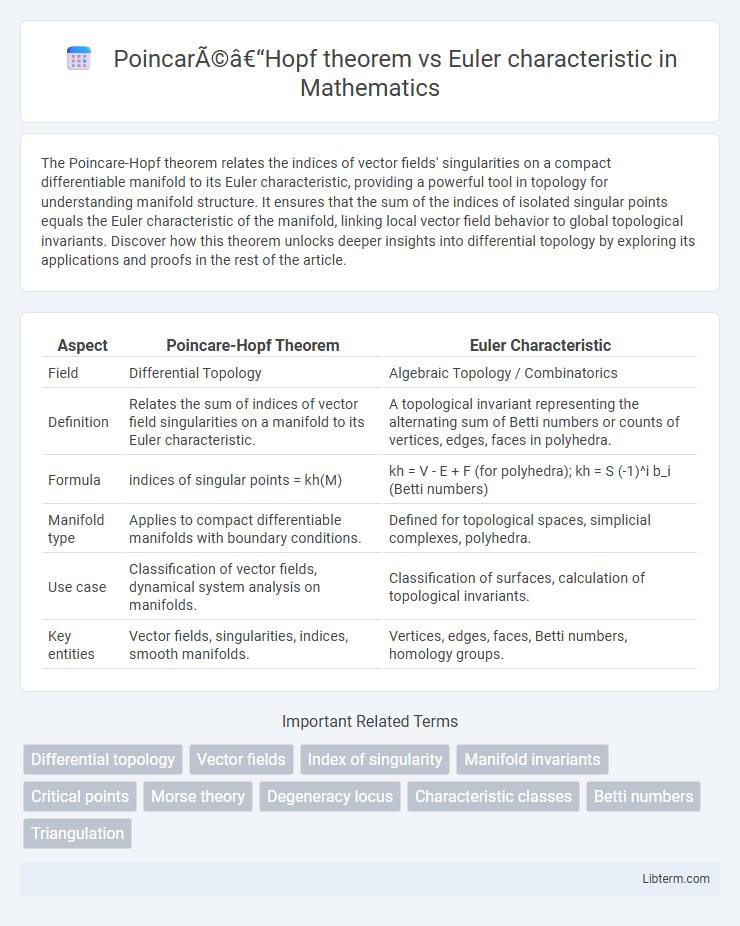
| Aspect | Poincare-Hopf Theorem | Euler Characteristic |
|---|---|---|
| Field | Differential Topology | Algebraic Topology / Combinatorics |
| Definition | Relates the sum of indices of vector field singularities on a manifold to its Euler characteristic. | A topological invariant representing the alternating sum of Betti numbers or counts of vertices, edges, faces in polyhedra. |
| Formula | indices of singular points = kh(M) | kh = V - E + F (for polyhedra); kh = S (-1)^i b_i (Betti numbers) |
| Manifold type | Applies to compact differentiable manifolds with boundary conditions. | Defined for topological spaces, simplicial complexes, polyhedra. |
| Use case | Classification of vector fields, dynamical system analysis on manifolds. | Classification of surfaces, calculation of topological invariants. |
| Key entities | Vector fields, singularities, indices, smooth manifolds. | Vertices, edges, faces, Betti numbers, homology groups. |
Introduction to Poincaré–Hopf Theorem and Euler Characteristic
The Poincare-Hopf theorem links the sum of indices of vector fields' isolated singularities on a compact manifold to the manifold's Euler characteristic, providing a powerful topological invariant relationship. The Euler characteristic serves as a fundamental topological invariant representing the shape's intrinsic properties, computed as V - E + F for polyhedra or generalized via homology for higher-dimensional spaces. By connecting vector field behavior to the Euler characteristic, the Poincare-Hopf theorem offers a profound insight into the interplay between topology and differential geometry.
Historical Background and Mathematical Context
The Poincare-Hopf theorem, developed by Henri Poincare and Heinz Hopf in the early 20th century, links vector field behavior on differentiable manifolds to topological invariants, specifically the Euler characteristic. The Euler characteristic, introduced by Leonhard Euler in the 18th century through polyhedral formulae, serves as a fundamental invariant quantifying topological structure via vertices, edges, and faces. The theorem extends Euler's classical work by connecting fixed points or zeros of vector fields to this topological invariant, providing a profound interplay between differential topology and algebraic topology.
Fundamental Definitions: Vector Fields and Topology
The Poincare-Hopf theorem establishes a fundamental link between vector fields on a smooth, compact manifold and the manifold's Euler characteristic by relating the sum of indices of isolated zeros of a vector field to the Euler characteristic. Vector fields describe directions of flow at each point, while topology classifies the manifold's shape and structure, encapsulated by invariants such as the Euler characteristic, which counts vertices minus edges plus faces in a simplicial complex. This theorem bridges differential topology and algebraic topology by using indices of singularities in vector fields to capture a topological invariant, demonstrating the interplay between local geometric properties and global topological invariants.
The Euler Characteristic: Concept and Computation
The Euler characteristic is a topological invariant defined as the alternating sum of the numbers of vertices, edges, and faces in a polyhedral object, often computed as kh = V - E + F. In the context of surfaces, this characteristic helps classify shapes by summarizing their intrinsic topology, independent of deformation. The Poincare-Hopf theorem connects the Euler characteristic to vector fields by equating it with the sum of indices of singularities of a vector field on a manifold, bridging combinatorial topology and differential geometry.
Statement and Interpretation of the Poincaré–Hopf Theorem
The Poincare-Hopf theorem states that for a compact differentiable manifold, the sum of the indices of isolated zeros of a vector field equals the Euler characteristic of the manifold. This theorem provides a direct link between differential topology and the topological invariant Euler characteristic, interpreting vector field behavior through global geometric properties. The interpretation emphasizes that the topological structure of a manifold constrains vector field singularities, offering a powerful tool for understanding manifold geometry via index theory.
Comparing Theorem and Characteristic: Key Differences
The Poincare-Hopf theorem establishes a direct link between the sum of the indices of vector field singularities on a smooth manifold and its Euler characteristic, providing a geometric interpretation of this topological invariant. Unlike the Euler characteristic, which is a purely combinatorial or topological quantity computed from simplicial complexes or cell decompositions, the theorem uses differential topology to relate vector fields' behavior to topological properties. This distinction highlights the theorem's role in connecting analysis and topology, whereas the Euler characteristic serves as a fundamental descriptor of a space's shape and structure independently of vector fields.
Applications in Topology and Geometry
The Poincare-Hopf theorem relates the sum of the indices of vector fields' singularities on a compact, differentiable manifold to the manifold's Euler characteristic, providing a powerful tool for classifying topological spaces. In geometry, this theorem aids in understanding curvature and critical points, while in topology, it is essential for analyzing vector bundles, fixed points, and surface invariants. The interplay between the theorem and the Euler characteristic enables precise computations in manifold classification, surface genus determination, and the study of dynamical systems on manifolds.
Illustrative Examples and Case Studies
The Poincare-Hopf theorem relates vector fields on smooth manifolds to the Euler characteristic by equating the sum of the indices of isolated singularities of a vector field to the Euler characteristic of the manifold. For instance, on a 2-sphere, a vector field with isolated zeroes has indices summing to 2, matching the sphere's Euler characteristic. Case studies on toroidal surfaces show that vector fields without singularities yield an Euler characteristic of zero, illustrating the theorem's applicability in different topological settings.
Limitations and Generalizations
The Poincare-Hopf theorem, which relates the sum of the indices of vector field singularities to the Euler characteristic, is limited to compact, differentiable manifolds with isolated singularities. It does not directly apply to non-compact manifolds, manifolds with boundary, or singularities of higher complexity, requiring extensions or adaptations. Generalizations include the Lefschetz fixed-point theorem and extensions to orbifolds and stratified spaces, broadening applications beyond classical smooth manifold settings.
Conclusion: Insights from the Poincaré–Hopf–Euler Relationship
The Poincare-Hopf theorem establishes a fundamental link between the sum of the indices of vector field singularities on a manifold and its Euler characteristic, revealing deep topological insights. This relationship implies that vector field behavior encodes intrinsic geometric properties, enabling classification of surfaces and higher-dimensional analogs. Understanding this connection enhances analysis in differential topology, dynamical systems, and geometry by bridging local singularities with global topological invariants.
Poincaré–Hopf theorem Infographic
 libterm.com
libterm.com