A bicategory generalizes the concept of a category by allowing morphisms between morphisms, called 2-morphisms, which provide a richer structure for mathematical and computational frameworks. Your understanding of bicategories can enhance the study of higher-dimensional algebra and category theory, offering powerful tools for diagrammatic reasoning and composition. Dive into the rest of the article to explore the detailed properties, examples, and applications of bicategories.
Table of Comparison
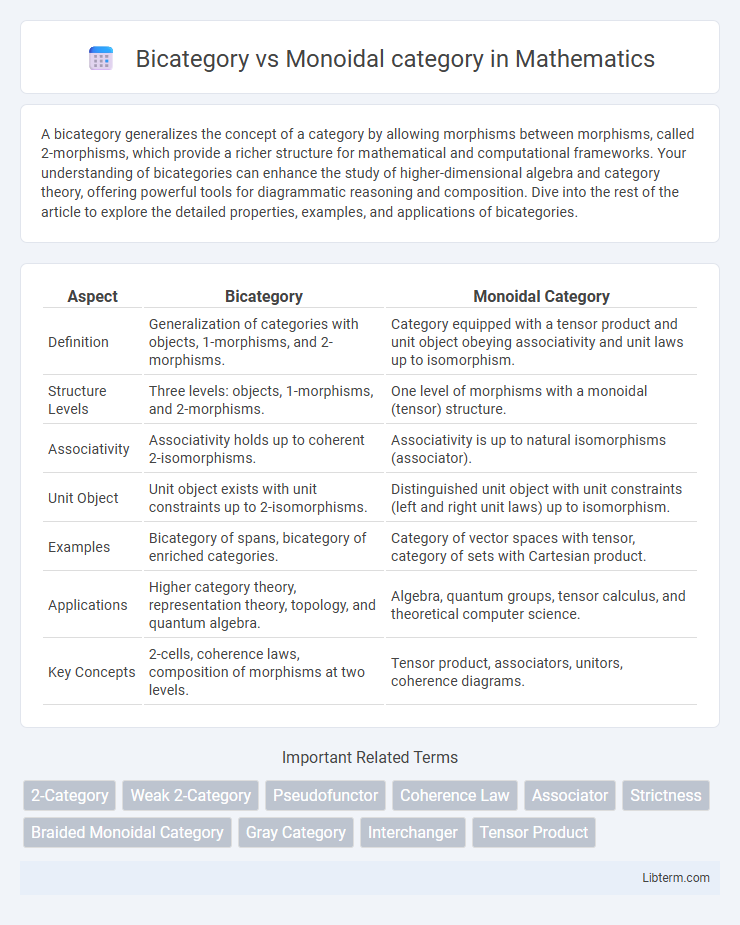
| Aspect | Bicategory | Monoidal Category |
|---|---|---|
| Definition | Generalization of categories with objects, 1-morphisms, and 2-morphisms. | Category equipped with a tensor product and unit object obeying associativity and unit laws up to isomorphism. |
| Structure Levels | Three levels: objects, 1-morphisms, and 2-morphisms. | One level of morphisms with a monoidal (tensor) structure. |
| Associativity | Associativity holds up to coherent 2-isomorphisms. | Associativity is up to natural isomorphisms (associator). |
| Unit Object | Unit object exists with unit constraints up to 2-isomorphisms. | Distinguished unit object with unit constraints (left and right unit laws) up to isomorphism. |
| Examples | Bicategory of spans, bicategory of enriched categories. | Category of vector spaces with tensor, category of sets with Cartesian product. |
| Applications | Higher category theory, representation theory, topology, and quantum algebra. | Algebra, quantum groups, tensor calculus, and theoretical computer science. |
| Key Concepts | 2-cells, coherence laws, composition of morphisms at two levels. | Tensor product, associators, unitors, coherence diagrams. |
Introduction to Category Theory Concepts
Bicategories generalize monoidal categories by allowing composition of 1-morphisms to be associative and unital only up to specified 2-isomorphisms, rather than strictly. Monoidal categories consist of a single object with morphisms forming a category equipped with a tensor product and associativity constraints, serving as a foundational example of bicategories with one object. Understanding bicategories involves grasping the relaxation of strict associativity and identity laws present in monoidal categories, which are central concepts in category theory.
Defining Monoidal Categories
Monoidal categories consist of a category equipped with a tensor product, an identity object, and natural isomorphisms satisfying coherence conditions such as associativity and unit laws. These structures enable the representation of processes that combine objects while preserving their categorical properties. Unlike bicategories, which generalize categories by allowing morphisms between morphisms, monoidal categories focus on a single layer of morphisms complemented by tensor operations.
Key Properties of Monoidal Categories
Monoidal categories feature a tensor product that is associative up to natural isomorphism and possess a unit object acting as an identity for the tensor product. Their coherence laws, captured by Mac Lane's pentagon and triangle identities, ensure the consistency of associativity and unit constraints. Unlike bicategories, which generalize composition allowing morphisms between morphisms, monoidal categories emphasize a single binary operation with strict coherence conditions.
What is a Bicategory?
A bicategory generalizes a category by allowing morphisms between morphisms, called 2-morphisms, enabling composition that is associative and unital only up to coherent isomorphisms rather than strict equality. It consists of objects, 1-morphisms between objects, and 2-morphisms between 1-morphisms, providing a richer structure for modeling transformations in higher category theory. Unlike a monoidal category, which has a single object with a tensor product, bicategories accommodate multiple objects and complex compositional behavior essential for applications in topology, algebra, and theoretical computer science.
Structure and Components of Bicategories
Bicategories generalize monoidal categories by allowing morphisms between objects to form categories themselves, rather than mere sets of morphisms. The structure of a bicategory consists of objects, 1-morphisms (arrows between objects), and 2-morphisms (arrows between 1-morphisms) with composition operations associative up to specified natural isomorphisms called associators. Unlike monoidal categories, bicategories include coherence data such as associator and unit isomorphisms, enabling flexible composition and richer inter-layer morphism interactions.
Comparing Monoidal Categories and Bicategories
Monoidal categories consist of a single category equipped with a tensor product and associativity constraints, providing a framework for describing objects and morphisms with a single layer of composition. Bicategories generalize this structure by incorporating objects, 1-morphisms, and 2-morphisms with associativity and unit constraints defined up to coherent isomorphism, allowing for a richer composition framework across multiple layers. Comparing the two, monoidal categories can be seen as bicategories with one object, simplifying the complexity of morphisms but limiting higher-dimensional algebraic structures.
Examples of Monoidal Categories
Examples of monoidal categories include the category of vector spaces over a field with the tensor product serving as the monoidal operation and the field as the unit object, and the category of sets equipped with the Cartesian product as the monoidal product and a singleton set as the identity. Another key example is the category of chain complexes of modules over a ring, where the monoidal structure arises from the tensor product of complexes. These examples highlight monoidal categories as frameworks for structures that support an associative tensor-like product and a distinguished unit object.
Examples of Bicategories
Bicategories generalize monoidal categories by allowing morphisms between morphisms, making them useful in contexts such as the bicategory of small categories, functors, and natural transformations. Another key example is the bicategory Span, where objects are sets, morphisms are spans, and 2-morphisms are maps between spans, often used to model relationships in algebraic geometry and topology. These examples highlight how bicategories provide a richer structure than monoidal categories by incorporating higher-dimensional morphisms.
Applications in Mathematics and Physics
Bicategories generalize monoidal categories by allowing morphisms between morphisms, enriching the structure used in higher-dimensional category theory and quantum field theory. In mathematics, bicategories facilitate the study of homotopy theory and higher algebra, while monoidal categories effectively model tensor products and symmetric structures in representation theory. Physics applications include bicategories in topological quantum field theories and monoidal categories in describing particle interactions and quantum symmetries.
Summary: Choosing Between Bicategory and Monoidal Category
Bicategories generalize monoidal categories by allowing morphisms between morphisms, enabling more flexible compositional structures useful in higher category theory and enriched category contexts. Monoidal categories represent simpler algebraic structures with a single associative tensor product and unit object, ideal for tensor calculus, quantum computing, and basic categorical algebra. Selecting bicategories suits complex hierarchical or multi-level transformations, while monoidal categories suffice for applications emphasizing a single, consistent tensor operation.
Bicategory Infographic
 libterm.com
libterm.com