The least upper bound, also known as the supremum, is the smallest value that is greater than or equal to every element in a given set. It plays a crucial role in mathematical analysis, particularly in understanding limits and convergence of sequences. Explore the rest of the article to deepen your grasp of how least upper bounds apply across different mathematical contexts.
Table of Comparison
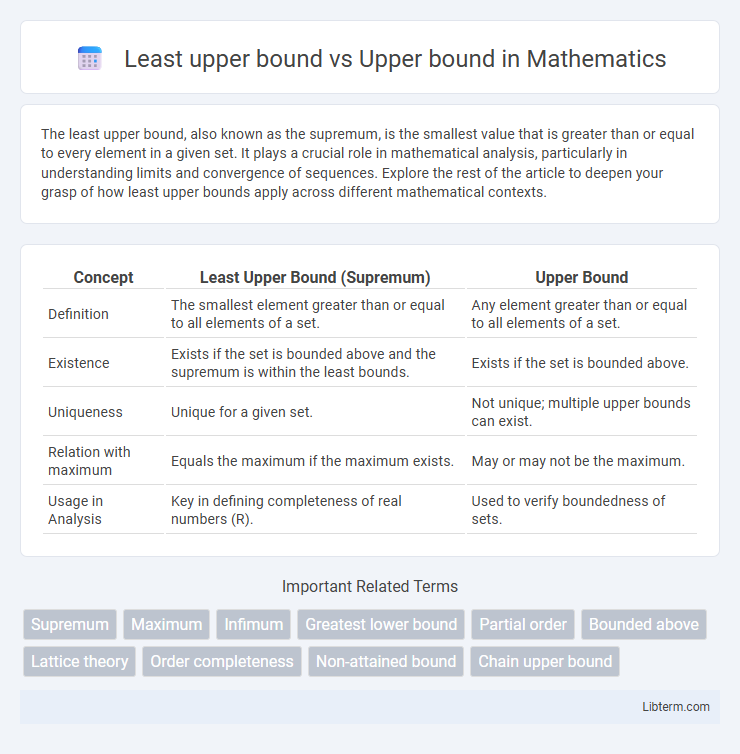
| Concept | Least Upper Bound (Supremum) | Upper Bound |
|---|---|---|
| Definition | The smallest element greater than or equal to all elements of a set. | Any element greater than or equal to all elements of a set. |
| Existence | Exists if the set is bounded above and the supremum is within the least bounds. | Exists if the set is bounded above. |
| Uniqueness | Unique for a given set. | Not unique; multiple upper bounds can exist. |
| Relation with maximum | Equals the maximum if the maximum exists. | May or may not be the maximum. |
| Usage in Analysis | Key in defining completeness of real numbers (R). | Used to verify boundedness of sets. |
Introduction to Upper Bounds and Least Upper Bounds
Upper bounds in mathematics represent values that are greater than or equal to every element in a given set, providing a threshold that the elements do not exceed. The least upper bound, or supremum, is the smallest such value, ensuring it is less than or equal to all other upper bounds while still being an upper bound itself. Understanding the distinction between upper bounds and least upper bounds is essential in analysis, particularly in studying limits, convergence, and completeness of ordered sets.
Definitions: Upper Bound and Least Upper Bound
An upper bound of a set is any value that is greater than or equal to every element in that set, ensuring no element exceeds it. The least upper bound, also known as the supremum, is the smallest value among all upper bounds, tightly enclosing the set from above without being smaller than any other upper bound. These concepts are fundamental in order theory and real analysis, particularly for defining limits and bounds in partially ordered sets and the real number system.
Key Differences Between Upper Bound and Least Upper Bound
An upper bound is any value that is greater than or equal to every element in a set, while the least upper bound (also called the supremum) is the smallest such value. Every least upper bound is an upper bound, but not every upper bound qualifies as a least upper bound. The key difference lies in minimality: the least upper bound is the minimal upper bound that tightly encloses the set without excluding any smaller candidates.
Mathematical Representation of Upper Bounds
The upper bound of a set in mathematics is any value greater than or equal to every element of the set, denoted as \( b \geq x \) for all \( x \) in the set. The least upper bound, or supremum, is the smallest such value that still serves as an upper bound, formally \( \inf \{ b \in \mathbb{R} : b \geq x \text{ for all } x \in S \} \). While every set with an upper bound has many upper bounds, the least upper bound uniquely minimizes this set of bounds and is crucial in analysis and order theory.
The Concept of Supremum Explained
The least upper bound, or supremum, of a set is the smallest value that is greater than or equal to every element in that set, making it a unique value if it exists. An upper bound is any value that is greater than or equal to all elements in the set but is not necessarily the smallest among such values. The supremum represents a precise concept in order theory and real analysis, crucial for defining limits, convergence, and completeness in mathematical structures.
Examples Illustrating Upper Bound vs Least Upper Bound
An upper bound of a set is any value greater than or equal to all elements in the set, such as 5 for the set {1, 3, 4}, while the least upper bound (or supremum) is the smallest such value, like 4 in this example. For instance, in the set {x R | x < 3}, the number 4 is an upper bound, but the least upper bound is 3, which is not in the set yet is the minimal boundary. Understanding how upper bounds and least upper bounds operate clarifies concepts in analysis and set theory, especially when dealing with open or closed sets.
Importance of Upper Bounds in Real Analysis
Upper bounds in real analysis provide critical limitations on the range of a set, ensuring that all elements lie below or at a certain value, which is essential for defining convergence and limits. The least upper bound, or supremum, represents the smallest such boundary, offering a precise measure that can be fundamental in proving completeness properties of the real numbers. Identifying these bounds helps analyze functions, sequences, and sets, playing a central role in optimization and continuity arguments.
Applications of Least Upper Bound in Mathematics
The least upper bound (supremum) of a set is the smallest value that is greater than or equal to every element in that set, used extensively in real analysis and optimization problems to identify bounds that ensure convergence and stability. Unlike a general upper bound which can be any value exceeding all elements, the least upper bound provides a precise limit critical for defining limits, integrals, and completeness properties in ordered sets. Applications of the least upper bound include determining the supremum of sequences, ensuring the existence of limits in calculus, and evaluating bounds in functional analysis and probability theory.
Common Mistakes in Identifying Bounds
Confusing least upper bound (supremum) with any upper bound is a common mistake, as the supremum is the smallest of all upper bounds for a set and not just any element greater than or equal to all elements in the set. Misidentifying an upper bound as the least upper bound occurs when the precise infimum of the upper bounds is overlooked, especially in sets without a maximum element. Another frequent error involves neglecting that the supremum may not belong to the set, leading to incorrect assumptions about its membership or boundary properties.
Conclusion: Comparing Least Upper Bound and Upper Bound
The least upper bound (supremum) is the smallest value that is greater than or equal to every element in a set, whereas an upper bound can be any value exceeding all elements without the minimal requirement. The least upper bound provides a precise boundary critical in analysis and optimization, ensuring uniqueness and sharpness in results. Understanding this distinction is essential for accurate mathematical modeling and guarantees optimal solution characterization.
Least upper bound Infographic
 libterm.com
libterm.com