Simple solutions often bring the most effective results by focusing on clarity and ease of use. Streamlining processes helps reduce confusion and boosts productivity, making everyday tasks more manageable for you. Explore the rest of the article to discover practical tips that simplify your life.
Table of Comparison
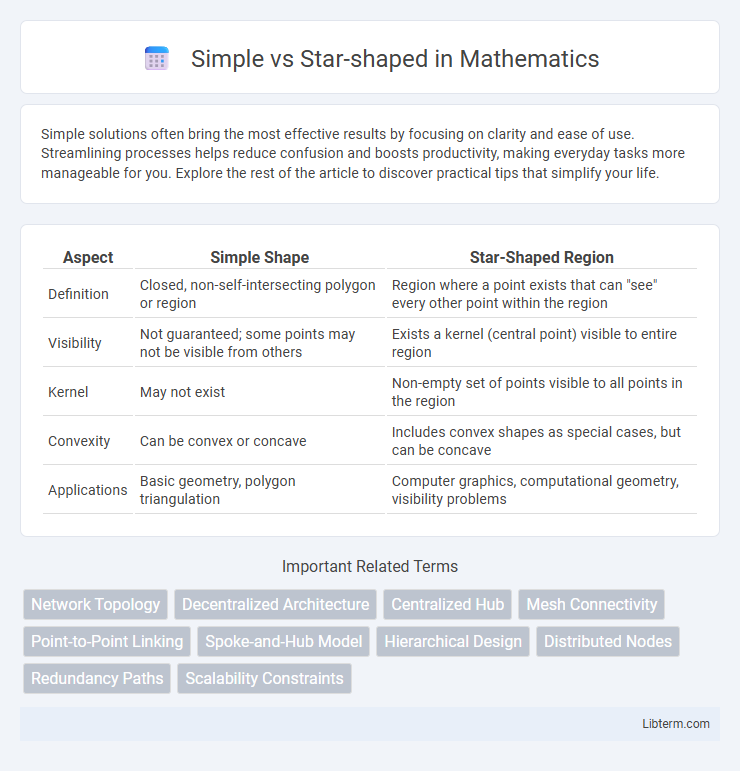
| Aspect | Simple Shape | Star-Shaped Region |
|---|---|---|
| Definition | Closed, non-self-intersecting polygon or region | Region where a point exists that can "see" every other point within the region |
| Visibility | Not guaranteed; some points may not be visible from others | Exists a kernel (central point) visible to entire region |
| Kernel | May not exist | Non-empty set of points visible to all points in the region |
| Convexity | Can be convex or concave | Includes convex shapes as special cases, but can be concave |
| Applications | Basic geometry, polygon triangulation | Computer graphics, computational geometry, visibility problems |
Understanding Simple and Star-shaped Concepts
Simple shapes consist of basic geometric forms like circles, squares, and triangles that have clear boundaries and minimal complexity. Star-shaped shapes are defined by a center point from which every boundary point is directly visible without intersecting the interior, making them a subset of convex shapes. Understanding star-shaped concepts is essential in fields like computational geometry and computer graphics, where visibility and shape properties impact algorithms and visual rendering.
Key Differences Between Simple and Star-shaped Structures
Simple structures, characterized by straightforward linear or branching forms, allow direct load transfer with minimal internal complexity and are commonly used in small buildings. Star-shaped structures feature multiple radial elements extending from a central core, enhancing load distribution and providing increased stability in large-scale or high-rise constructions. The key difference lies in complexity and load management: simple structures prioritize simplicity and ease of construction, while star-shaped designs optimize structural performance under diverse stress conditions.
Advantages of Simple Shapes
Simple shapes offer advantages in design clarity and ease of recognition, facilitating quick visual interpretation for users. Their geometric consistency enhances scalability and adaptability across various digital and print media. Simple shapes also reduce cognitive load, improving user experience by enabling faster comprehension and interaction.
Advantages of Star-shaped Designs
Star-shaped designs offer enhanced structural stability and improved load distribution compared to simple layouts, increasing overall durability. Their geometric configuration allows for efficient space utilization and better natural ventilation, which can reduce energy costs. These designs also provide greater aesthetic appeal, often leading to higher property value and market interest.
Applications in Mathematics and Geometry
Simple polygons serve as foundational structures in computational geometry, enabling algorithms for area calculation, point-in-polygon tests, and mesh generation. Star-shaped polygons extend these applications by allowing every point within the polygon to be visible from a central kernel, facilitating optimized pathfinding, visibility analysis, and robot motion planning. Understanding the distinction between simple and star-shaped polygons enhances problem-solving in geographic information systems (GIS), computer graphics, and spatial data modeling.
Use Cases in Computer Science and Data Structures
Simple graphs are often utilized in computer science for representing undirected relationships without multiple edges or loops, making them ideal for social networks and communication models. Star-shaped graphs are specialized data structures where a central node connects to peripheral nodes, optimizing use cases such as hub-and-spoke network topologies and central server-client architectures. Choosing between simple and star-shaped graphs depends on the need for straightforward connectivity versus centralized control and rapid access patterns.
Visual Representation: Simple vs Star-shaped
Simple visual representations consist of straightforward, linear structures that emphasize clarity and ease of understanding, often using basic shapes such as circles or rectangles connected by single lines. Star-shaped visual representations highlight a central node with multiple spokes radiating outward, emphasizing the central element's connections and influence within the network. This layout enhances the perception of hierarchy and centrality, making it ideal for illustrating relationships where one element dominates or coordinates others.
Practical Examples in Real-life Scenarios
Simple networks often appear in home Wi-Fi setups where devices connect directly to a single router, providing straightforward management and minimal hardware costs. Star-shaped networks dominate office environments, linking multiple workstations through a central switch or hub to enhance performance and simplify fault isolation. Real-life applications demonstrate that star topologies support scalability and reliability, while simple networks offer cost-effective solutions for smaller, less complex user groups.
Challenges and Limitations of Each Structure
Simple neural network structures face challenges such as limited capacity for handling complex patterns and reduced scalability when dealing with large datasets, leading to underfitting issues. Star-shaped networks, while offering better feature integration by connecting multiple inputs to a central node, suffer from bottlenecks at the hub, resulting in potential information loss and increased computational complexity. Both architectures display limitations in adaptability and robustness, requiring careful design choices to balance efficiency and learning performance.
Choosing the Right Form: Which to Use and When
Choosing between simple and star-shaped network topologies depends on the specific needs of the system's scale, complexity, and fault tolerance. Simple topologies offer ease of setup and efficient communication for small-scale applications, while star-shaped topologies provide centralized management and improved fault isolation, making them ideal for larger networks requiring robust performance. Evaluating factors such as network size, maintenance capabilities, and failure impact helps determine the optimal topology for reliable and scalable connectivity.
Simple Infographic
 libterm.com
libterm.com