Scheme is a minimalist dialect of the Lisp programming language known for its clean syntax and powerful features like first-class procedures and lexical scoping. Its simplicity makes it ideal for teaching programming concepts while also supporting advanced functional programming techniques. Explore the full article to discover how Scheme can enhance your coding skills and problem-solving abilities.
Table of Comparison
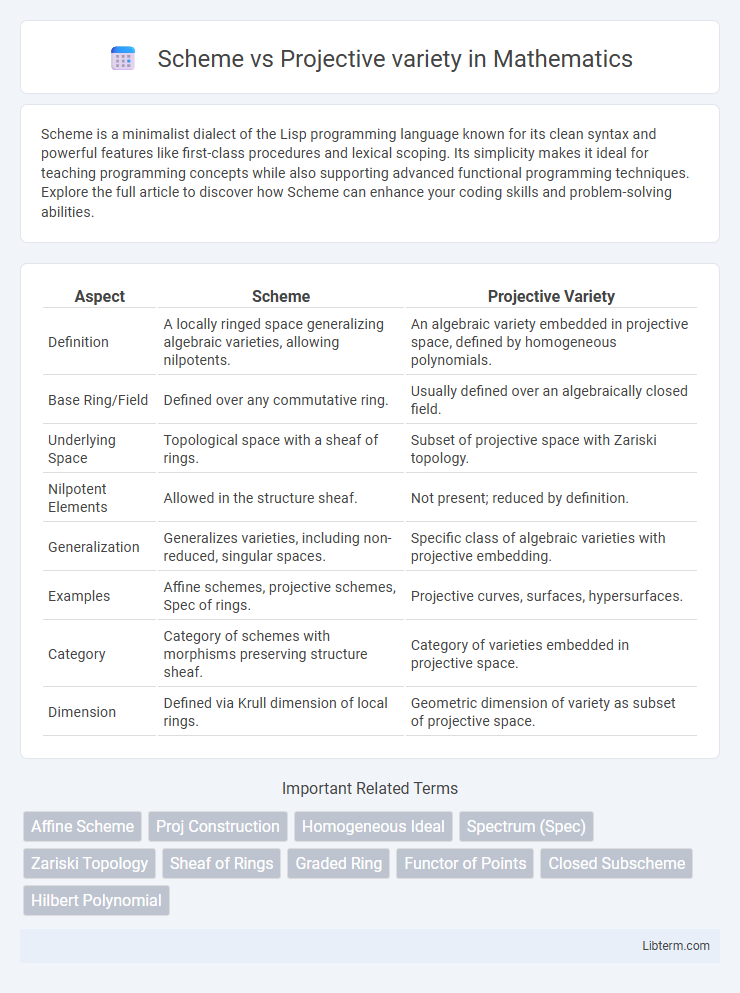
| Aspect | Scheme | Projective Variety |
|---|---|---|
| Definition | A locally ringed space generalizing algebraic varieties, allowing nilpotents. | An algebraic variety embedded in projective space, defined by homogeneous polynomials. |
| Base Ring/Field | Defined over any commutative ring. | Usually defined over an algebraically closed field. |
| Underlying Space | Topological space with a sheaf of rings. | Subset of projective space with Zariski topology. |
| Nilpotent Elements | Allowed in the structure sheaf. | Not present; reduced by definition. |
| Generalization | Generalizes varieties, including non-reduced, singular spaces. | Specific class of algebraic varieties with projective embedding. |
| Examples | Affine schemes, projective schemes, Spec of rings. | Projective curves, surfaces, hypersurfaces. |
| Category | Category of schemes with morphisms preserving structure sheaf. | Category of varieties embedded in projective space. |
| Dimension | Defined via Krull dimension of local rings. | Geometric dimension of variety as subset of projective space. |
Introduction to Schemes and Projective Varieties
Schemes generalize algebraic varieties by allowing local affine patches to be spectra of rings, enabling the study of solutions to polynomial equations with nilpotent elements and over arbitrary rings. Projective varieties are defined as the zero loci of homogeneous polynomials in projective space, providing a classical framework for irreducible algebraic sets with well-understood geometric properties. The scheme-theoretic approach extends projective varieties by incorporating both underlying topological spaces and structure sheaves, facilitating a deeper understanding of geometric and arithmetic aspects in algebraic geometry.
Historical Context and Motivation
The development of schemes arose from the limitations of classical algebraic geometry in handling singularities and non-algebraically closed fields, extending the concept of projective varieties by incorporating nilpotent elements and allowing local algebraic structures. Projective varieties, deeply rooted in the 19th-century work of mathematicians like Riemann and projective geometers, were defined as zero loci of homogeneous polynomials in projective space, emphasizing a rigid geometric viewpoint. Grothendieck's introduction of schemes in the 1960s revolutionized algebraic geometry by providing a unifying framework that generalized projective varieties and enabled advanced techniques like cohomology and duality theories.
Definitions: Schemes in Algebraic Geometry
A scheme in algebraic geometry is a locally ringed space that generalizes algebraic varieties by patching together spectra of rings, allowing the treatment of singularities and more general solutions. Projective varieties are specific types of algebraic varieties defined as zero loci of homogeneous polynomials in projective space, exhibiting properties tied to compactness and embedding. Schemes extend the concept of projective varieties by encompassing both affine and projective cases as local models, providing a more flexible framework for studying geometric objects through their underlying rings.
Understanding Projective Varieties
Projective varieties are subsets of projective space defined as the zero loci of homogeneous polynomials, making them fundamental objects in algebraic geometry. Unlike schemes, which generalize algebraic varieties by incorporating nilpotent elements and non-reduced structures, projective varieties emphasize geometric intuition through their embedding into projective space. The study of projective varieties involves understanding their dimensions, singularities, and morphisms, typically using tools such as graded coordinate rings and sheaf cohomology.
Key Differences Between Schemes and Projective Varieties
Schemes generalize varieties by allowing nilpotent elements in their structure sheaf, while projective varieties are reduced, irreducible algebraic sets embedded in projective space. Schemes use a broader sheaf-theoretic framework enabling the study of more general geometric objects, including those with singularities and non-reduced structures. Projective varieties, defined by homogeneous polynomials, have a fixed embedding in projective space, whereas schemes can exist abstractly without such embeddings.
Affine vs Projective Geometry: A Comparative Overview
Affine geometry studies algebraic varieties defined by polynomial equations within affine space, characterized by coordinate rings and local properties without points at infinity, making it suitable for working with affine schemes in commutative algebra. Projective geometry extends affine concepts to projective space by adding points at infinity, leading to projective varieties defined by homogeneous coordinates and graded rings, which provide compactness and ensure properties like completeness. Comparing schemes over affine and projective varieties underscores the role of local versus global properties, where affine schemes correspond to spectra of rings focusing on local behavior, while projective schemes incorporate global sections of graded rings, emphasizing the interplay between algebraic and geometric structures in extended homogeneous spaces.
Examples Illustrating Schemes and Projective Varieties
The projective variety defined by the zero set of homogeneous polynomials in projective space, such as the projective plane curve given by the homogeneous polynomial f(x,y,z)=x^2 + y^2 - z^2, exemplifies classical algebraic geometry. In contrast, schemes broaden this concept by incorporating nilpotent elements and allowing local rings, for example, the spectrum of the ring k[x]/(x^2), which represents a non-reduced scheme with a single underlying point but richer structure than a simple variety. These examples highlight the flexibility of schemes in capturing infinitesimal information absent in the classical projective variety framework.
Applications in Modern Algebraic Geometry
Scheme theory generalizes projective varieties by incorporating nilpotent elements and allowing more flexible local structures, making it fundamental for modern algebraic geometry. Schemes enable the rigorous treatment of phenomena such as singularities, intersection theory, and moduli problems that projective varieties alone cannot fully address. This robustness supports advances in number theory, deformation theory, and arithmetic geometry, where classical projective varieties provide an insufficient framework.
Bridging Schemes and Projective Varieties: Morphisms and Maps
Schemes generalize projective varieties by allowing local ringed space structures that incorporate both algebraic and topological data, enabling more flexible morphisms beyond classical projective maps. Morphisms between schemes extend the concept of regular maps on projective varieties, often realized by ring homomorphisms that respect sheaf structures, thus bridging the intrinsic geometric properties with algebraic formulations. Projective schemes serve as a natural platform connecting classical projective varieties with modern scheme theory, preserving projective embedding notions while supporting more general morphisms and moduli interpretations.
Conclusion: Significance in Algebraic Geometry
Schemes generalize projective varieties by incorporating nilpotent elements and allowing for more flexible local behavior, enabling a richer and more comprehensive framework in algebraic geometry. Projective varieties remain fundamental for their classical geometric insights and explicit embeddings into projective space, serving as concrete examples within the broader schematic perspective. The significance lies in schemes' ability to unify diverse geometric phenomena, extend intersection theory, and facilitate modern advancements such as moduli spaces and cohomological methods.
Scheme Infographic
 libterm.com
libterm.com