A closed set in mathematics is a set that contains all its limit points, meaning it includes the boundaries of the set. This property is essential in topology and analysis for understanding convergence and continuity. Explore the rest of the article to learn how closed sets impact various mathematical concepts and your problem-solving skills.
Table of Comparison
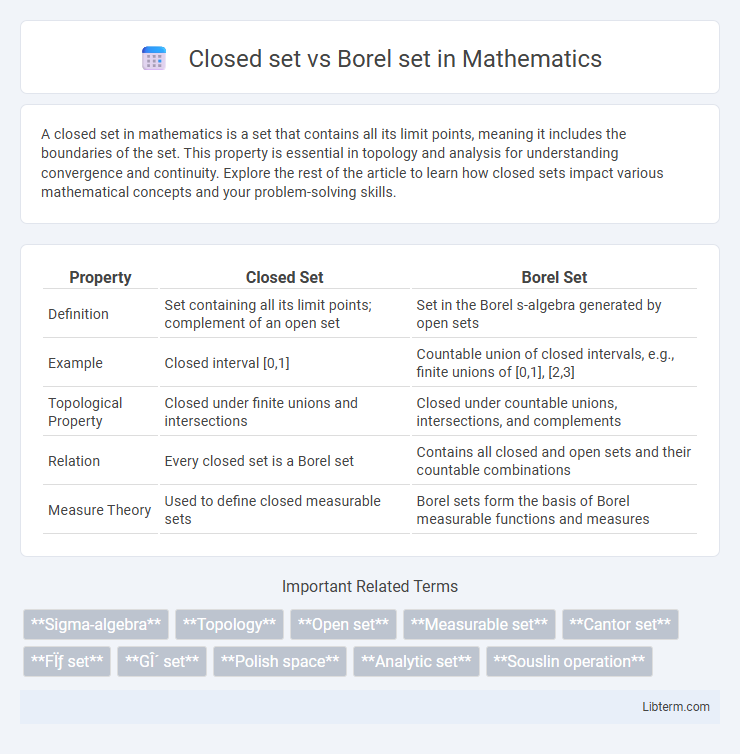
| Property | Closed Set | Borel Set |
|---|---|---|
| Definition | Set containing all its limit points; complement of an open set | Set in the Borel s-algebra generated by open sets |
| Example | Closed interval [0,1] | Countable union of closed intervals, e.g., finite unions of [0,1], [2,3] |
| Topological Property | Closed under finite unions and intersections | Closed under countable unions, intersections, and complements |
| Relation | Every closed set is a Borel set | Contains all closed and open sets and their countable combinations |
| Measure Theory | Used to define closed measurable sets | Borel sets form the basis of Borel measurable functions and measures |
Introduction to Closed Sets and Borel Sets
Closed sets in topology are defined as sets that contain all their limit points, making them complements of open sets within a given topological space. Borel sets are generated from open or closed sets through countable operations of union, intersection, and complementation, forming the smallest s-algebra containing all open sets. Understanding closed sets is fundamental to grasping Borel sets, as they serve as building blocks in the construction of Borel s-algebras used in measure theory and probability.
Defining Closed Sets in Topology
Closed sets in topology are defined as the complement of open sets within a given topological space, meaning a set is closed if its complement is open. Borel sets originate from the Borel s-algebra, generated by open sets through countable unions, intersections, and complementation, which include all open and closed sets as fundamental elements. Understanding closed sets is crucial in topology for characterizing limit points, continuity, and convergence within various spaces.
Understanding Borel Sets: An Overview
Borel sets form the smallest s-algebra containing all open sets in a given topological space, making them fundamental in measure theory and probability. Closed sets, being complements of open sets, are inherently part of the Borel s-algebra and illustrate the set's closure properties under complementation. Understanding Borel sets involves recognizing their generation from open and closed sets through countable unions, intersections, and complements, enabling the definition of measurable functions and probability measures.
Key Differences Between Closed Sets and Borel Sets
Closed sets are specific subsets of a topological space that contain all their limit points, making them complements of open sets, whereas Borel sets form a broader s-algebra generated by open or closed sets through countable unions, intersections, and complements. Closed sets are always Borel sets, but Borel sets include many sets that are neither open nor closed, such as sets formed via complex countable operations on open or closed sets. The key difference lies in closed sets being topologically defined and minimal, while Borel sets encompass a far richer hierarchy essential for measure theory and probability.
Properties of Closed Sets
Closed sets are characterized by containing all their limit points and being equal to their own closure, ensuring stability under limit operations in metric spaces. They are complements of open sets and exhibit important properties such as being closed under finite intersections and arbitrary unions. In topology and measure theory, closed sets play a crucial role in defining Borel sets, as Borel s-algebras are generated from open (and equivalently closed) sets through countable operations.
Properties of Borel Sets
Borel sets are generated from open sets through countable unions, intersections, and complements, forming the smallest sigma-algebra containing all open sets in a topological space. Unlike closed sets, which are complements of open sets, Borel sets include a broader collection of subsets, covering every open and closed set as well as sets constructed via countable operations on them. This flexibility makes Borel sets fundamental in measure theory, ensuring measurability and enabling the definition of Borel measures on spaces like the real line.
Hierarchies within Borel Sets
Closed sets form the foundation of the Borel hierarchy, appearing as the simplest Borel sets within the class of \(G_{\delta}\) sets. The Borel hierarchy classifies sets based on countable operations of unions and intersections starting from open or closed sets, resulting in complex levels denoted by \(\Sigma_n^0\) and \(\Pi_n^0\). Higher levels in the hierarchy represent increasingly intricate Borel sets, revealing rich structural properties critical in descriptive set theory and measurable function analysis.
Examples Illustrating Closed Sets vs Borel Sets
Closed sets in a topological space include examples like the interval [0,1] in the real numbers, while Borel sets encompass all sets generated from open sets through countable unions, intersections, and complements, such as the union of [0,1] and (2,3). Another example involves the Cantor set, which is closed and also a Borel set, but certain pathological sets constructed via transfinite operations in descriptive set theory are Borel sets that are not closed. These distinctions highlight that every closed set is a Borel set, but not every Borel set is closed, demonstrating the broader complexity and hierarchy within Borel sigma-algebras.
Applications in Measure Theory and Analysis
Closed sets serve as fundamental building blocks in topology and are crucial in defining measurable sets through their role in Borel s-algebras, which generate Borel sets as the smallest s-algebra containing all open (and thus all closed) sets. Borel sets enable the extension of measures defined on open or closed sets to more complex sets, facilitating the construction of Borel measures like Lebesgue measure, essential for integration theory and probability. Applications of closed and Borel sets in measure theory include the precise characterization of measurable functions, convergence theorems, and the foundation for real analysis, especially in handling limits, continuity, and differentiability within measurable spaces.
Summary: Choosing Between Closed and Borel Sets
Closed sets are fundamental in topology and analysis, characterized by containing all their limit points, making them essential for defining continuity and convergence. Borel sets, generated from open and closed sets through countable unions, intersections, and complements, form the backbone of measure theory and support defining measurable functions. Choosing between closed and Borel sets depends on the context: closed sets suit topological and convergence properties, while Borel sets are crucial for measurable spaces and probability applications.
Closed set Infographic
 libterm.com
libterm.com