Perspective projection creates the illusion of depth by representing three-dimensional objects on a two-dimensional plane, making distant objects appear smaller than those nearby. This technique is fundamental in computer graphics, art, and photography for realistic image rendering. Discover how perspective projection enhances visual perception and its applications by exploring the rest of the article.
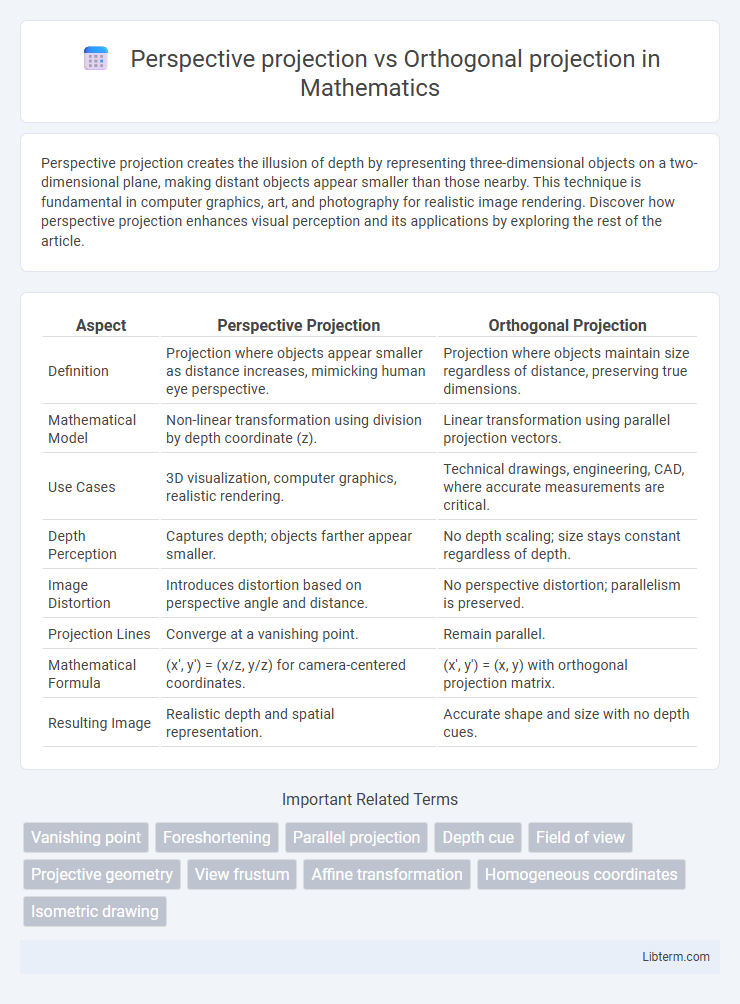
Table of Comparison
| Aspect | Perspective Projection | Orthogonal Projection |
|---|---|---|
| Definition | Projection where objects appear smaller as distance increases, mimicking human eye perspective. | Projection where objects maintain size regardless of distance, preserving true dimensions. |
| Mathematical Model | Non-linear transformation using division by depth coordinate (z). | Linear transformation using parallel projection vectors. |
| Use Cases | 3D visualization, computer graphics, realistic rendering. | Technical drawings, engineering, CAD, where accurate measurements are critical. |
| Depth Perception | Captures depth; objects farther appear smaller. | No depth scaling; size stays constant regardless of depth. |
| Image Distortion | Introduces distortion based on perspective angle and distance. | No perspective distortion; parallelism is preserved. |
| Projection Lines | Converge at a vanishing point. | Remain parallel. |
| Mathematical Formula | (x', y') = (x/z, y/z) for camera-centered coordinates. | (x', y') = (x, y) with orthogonal projection matrix. |
| Resulting Image | Realistic depth and spatial representation. | Accurate shape and size with no depth cues. |
Introduction to Projection Techniques
Perspective projection simulates how the human eye perceives depth, projecting 3D objects onto a 2D plane with converging lines that create a realistic sense of distance and scale. Orthogonal projection maintains parallel lines and true dimensions without perspective distortion, making it ideal for technical drawings and engineering designs. Both projection techniques are fundamental in computer graphics and CAD applications, enabling accurate visualization and analysis of spatial data.
What is Perspective Projection?
Perspective projection simulates the way the human eye perceives depth, where objects appear smaller as they move further away from the viewer, creating a sense of three-dimensionality on a two-dimensional plane. It uses a vanishing point and converging lines to represent spatial depth accurately in graphics and visualizations. This projection is essential in fields such as computer graphics, architectural rendering, and virtual reality for producing realistic images.
What is Orthogonal Projection?
Orthogonal projection is a type of parallel projection where objects are depicted without perspective distortion, maintaining true scale and shape regardless of depth. This projection method uses perpendicular projection lines to the projection plane, ensuring measurements remain consistent across the image. Orthogonal projection is commonly used in engineering and architectural drawings to provide accurate, measurable views of objects.
Key Differences Between Perspective and Orthogonal Projection
Perspective projection simulates human eye perception by depicting objects smaller as they recede into the distance, creating depth and realism in 3D rendering. Orthogonal projection maintains parallel lines without converging, preserving the actual dimensions of objects regardless of depth, commonly used in engineering and architectural drawings for accurate measurements. The key difference lies in perspective's depth distortion versus orthogonal's scale uniformity, impacting visual interpretation and spatial accuracy.
Mathematical Foundations of Each Projection
Perspective projection mathematically relies on the principles of projective geometry, where points are mapped onto a projection plane using lines converging at a single viewpoint or camera position, represented by a set of nonlinear transformations involving division by the depth coordinate (z). Orthogonal projection is based on linear algebra and Euclidean geometry, characterized by parallel projection lines perpendicular to the projection plane, modeled by simple linear transformations without depth scaling, preserving true object dimensions. The distinction lies in perspective projection's use of homogeneous coordinates and nonlinear perspective division compared to the orthogonal's straightforward matrix multiplication maintaining parallelism and scale.
Visual Outcomes and Real-World Applications
Perspective projection creates images with depth cues by converging parallel lines, making objects appear smaller as they distance from the viewer, crucial for realistic 3D rendering in video games and architectural visualization. Orthogonal projection maintains true object dimensions without distortion, preserving scale and shape, essential for engineering blueprints and technical drawings where precise measurements are critical. Visual outcomes differ as perspective projection enhances spatial perception, while orthogonal projection simplifies and clarifies structural details for exact real-world applications.
Advantages of Perspective Projection
Perspective projection offers a more realistic representation by mimicking the human eye's depth perception, making objects appear smaller as they get further away. It enhances spatial understanding in 3D modeling and virtual environments by providing depth cues and relative scaling. This projection is essential in applications like architectural visualization, gaming, and simulations where visual accuracy and immersion are critical.
Advantages of Orthogonal Projection
Orthogonal projection provides precise and undistorted representations of objects, maintaining true dimensions and angles, which is essential in technical drawings and engineering designs. This projection method simplifies measurements and construction by eliminating perspective foreshortening, ensuring accurate scale and alignment. Its ability to represent complex shapes clearly without distortion makes it a preferred choice for architectural plans and CAD models.
Use Cases in Computer Graphics and Engineering
Perspective projection is essential in computer graphics for creating realistic 3D visualizations, simulating how objects appear smaller as they recede into the distance, which is crucial in video games, virtual reality, and architectural renderings. Orthogonal projection is widely used in engineering and technical drawings because it maintains accurate scale and shape, enabling precise measurements and detailed representation of mechanical parts or building plans. Both projection methods complement each other by balancing visual realism and exact dimensional accuracy in different design and visualization workflows.
Choosing the Right Projection Method
Choosing the right projection method depends on the intended use and visual accuracy needed; perspective projection mimics human eye perception by converging lines and depth cues, making it ideal for realistic 3D visualization and architectural renderings. Orthogonal projection maintains object dimensions without distortion, ensuring precise measurements and scale representation, commonly preferred in engineering drawings and technical design. For applications requiring spatial accuracy and exact proportions, orthogonal projection is optimal, while perspective projection suits scenarios demanding immersive and natural visual experiences.
Perspective projection Infographic
 libterm.com
libterm.com