Markov processes describe systems that transition between states where future states depend only on the current state, not on the sequence of events that preceded it. This property, known as memorylessness, simplifies complex probabilistic modeling in fields like finance, genetics, and queueing theory. Explore the rest of the article to understand how Markov processes can be applied to your specific needs.
Table of Comparison
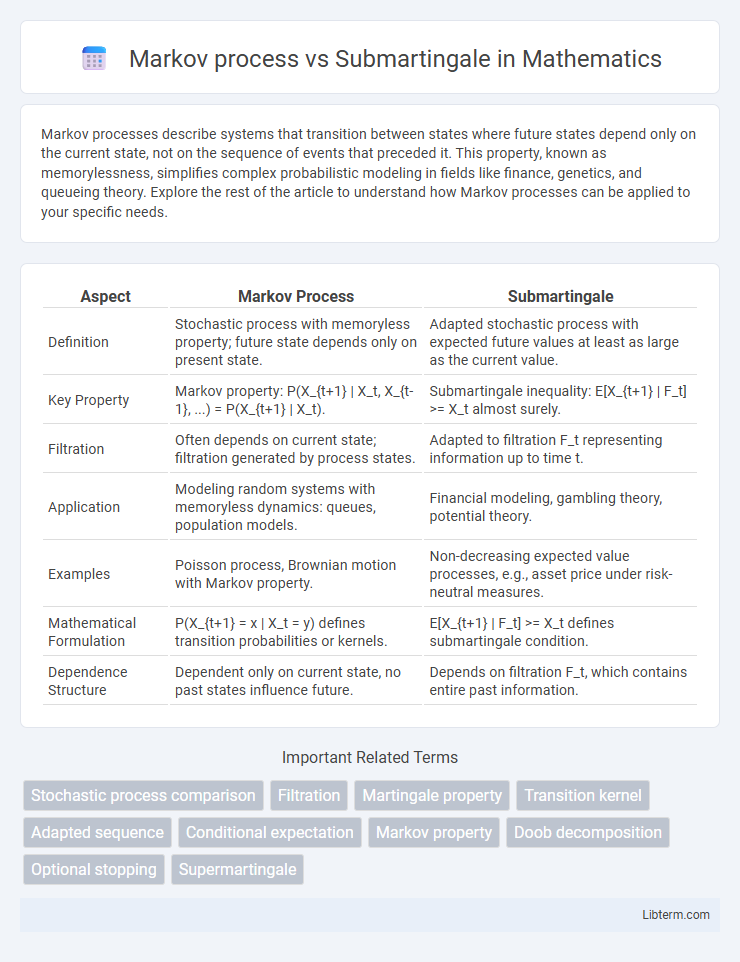
| Aspect | Markov Process | Submartingale |
|---|---|---|
| Definition | Stochastic process with memoryless property; future state depends only on present state. | Adapted stochastic process with expected future values at least as large as the current value. |
| Key Property | Markov property: P(X_{t+1} | X_t, X_{t-1}, ...) = P(X_{t+1} | X_t). | Submartingale inequality: E[X_{t+1} | F_t] >= X_t almost surely. |
| Filtration | Often depends on current state; filtration generated by process states. | Adapted to filtration F_t representing information up to time t. |
| Application | Modeling random systems with memoryless dynamics: queues, population models. | Financial modeling, gambling theory, potential theory. |
| Examples | Poisson process, Brownian motion with Markov property. | Non-decreasing expected value processes, e.g., asset price under risk-neutral measures. |
| Mathematical Formulation | P(X_{t+1} = x | X_t = y) defines transition probabilities or kernels. | E[X_{t+1} | F_t] >= X_t defines submartingale condition. |
| Dependence Structure | Dependent only on current state, no past states influence future. | Depends on filtration F_t, which contains entire past information. |
Introduction to Markov Processes and Submartingales
Markov processes describe stochastic systems where the future state depends only on the current state, emphasizing the memoryless property crucial for modeling random dynamics in fields like physics and finance. Submartingales are a class of stochastic processes characterized by their non-decreasing expected value conditional on the past, often used to model fair games or increasing trends in probability theory. Understanding the distinction between Markov processes and submartingales is essential for applying appropriate probabilistic tools in time-dependent stochastic modeling and risk assessment.
Key Definitions: Markov Process Explained
A Markov process is a stochastic model where future states depend solely on the current state, embodying the "memoryless" property crucial for predictions in probability theory. Submartingales are a class of stochastic processes characterized by an expected value that is non-decreasing over time, reflecting a trend that does not decline on average. While Markov processes focus on state transitions and conditional independence, submartingales emphasize expected value dynamics, making each concept essential for different aspects of stochastic modeling and analysis.
Key Definitions: Understanding Submartingales
A submartingale is a stochastic process {X_t} that satisfies the condition E[X_{t+1} | F_t] >= X_t, where F_t is the filtration representing the information up to time t, indicating that the conditional expectation of the next value is at least the current value. In contrast, a Markov process retains the property that the future state depends only on the present state, not on the past, defined by the Markov property P(X_{t+1} | X_t, X_{t-1}, ...) = P(X_{t+1} | X_t). While all Markov processes may not be submartingales, a submartingale's key feature is the non-decreasing expected value over time conditioned on past information.
Fundamental Properties of Markov Processes
Markov processes are characterized by the memoryless property, where the future state depends solely on the present state and not on the past trajectory, enabling a clear transition probability framework fundamental for modeling stochastic systems. Submartingales, by contrast, are stochastic processes with an expected increase conditioned on past information, emphasizing their role in modeling fair games or financial assets under uncertainty without the strict state-dependence of Markov processes. The fundamental properties of Markov processes include transition probability kernels, Chapman-Kolmogorov equations, and the strong Markov property, all critical for analyzing temporal evolution and prediction in diverse applications from physics to finance.
Fundamental Properties of Submartingales
Submartingales are stochastic processes characterized by the property that their conditional expected value, given past information, is at least as great as the current value, reflecting a non-decreasing trend in expectation. Unlike Markov processes, which depend solely on the current state and have the Markov property, submartingales emphasize expectation behavior and are integral in the theory of martingales and filtration. Fundamental properties of submartingales include the preservation of the submartingale property under stopping times and integrable increasing processes, making them crucial in areas like optimal stopping theory and financial mathematics.
Differences in Memory and Dependence Structures
Markov processes exhibit the memoryless property, where the future state depends solely on the present state, ensuring no influence from past states. Submartingales, however, embody a dependence structure based on conditional expectations, where future values are expected to increase given all past information. This fundamental difference highlights Markov processes' reliance on current state information versus submartingales' dependence on the entire filtration history.
Applications of Markov Processes in Real-World Problems
Markov processes model systems where future states depend only on the current state, making them essential in queueing theory, financial modeling, and genetics for predicting system evolution. Submartingales, often used in financial mathematics, focus on expected value increases and are key in option pricing and risk assessment. Markov processes excel in reliability engineering and inventory management by capturing memoryless property dynamics, enabling efficient decision-making under uncertainty.
Applications of Submartingales in Financial Modeling
Submartingales play a crucial role in financial modeling by providing a mathematical framework to represent asset prices that tend to increase on average over time, aligning with the concept of fair game investments exhibiting positive expected growth. Unlike Markov processes, which rely solely on the current state for future predictions, submartingales emphasize the conditional expectation structure underpinning price dynamics in markets with arbitrage considerations. Key applications include option pricing, risk management, and portfolio optimization, where submartingale properties ensure no-arbitrage conditions and model realistic price evolution under stochastic processes.
Comparative Analysis: Markov Processes vs Submartingales
Markov processes are characterized by the memoryless property where future states depend solely on the current state, while submartingales are stochastic processes defined by the conditional expectation of future values being at least as large as the present value, emphasizing non-decreasing trends. In terms of applications, Markov processes are often utilized for modeling systems with state transitions such as queuing theory and population dynamics, whereas submartingales play a crucial role in financial mathematics, particularly in option pricing and risk assessment due to their inherent properties of expected value growth. The comparative analysis highlights that Markov processes focus on state-dependent transitions, whereas submartingales emphasize expected value inequalities over time, making each suited for distinct classes of probabilistic modeling and optimization problems.
Conclusion: Choosing the Right Stochastic Framework
Selecting between a Markov process and a submartingale depends on the specific properties required for modeling stochastic behavior; Markov processes emphasize memoryless state transitions ideal for time-homogeneous systems, while submartingales capture non-decreasing expected values suited for modeling growth or fairness in stochastic environments. Understanding the underlying conditional expectations and filtration structures is crucial in determining the appropriate framework for applications in finance, economics, or engineering. Optimal choice ensures accurate representation of dynamics, improved predictive power, and analytical tractability tailored to the problem's probabilistic nature.
Markov process Infographic
 libterm.com
libterm.com