A singular vector is a fundamental concept in linear algebra associated with singular value decomposition (SVD), representing the directions along which a matrix acts by stretching or compressing. These vectors provide critical insights into the structure and properties of a matrix, aiding in tasks such as dimensionality reduction, image compression, and noise reduction. Explore the rest of the article to deepen your understanding of singular vectors and their practical applications.
Table of Comparison
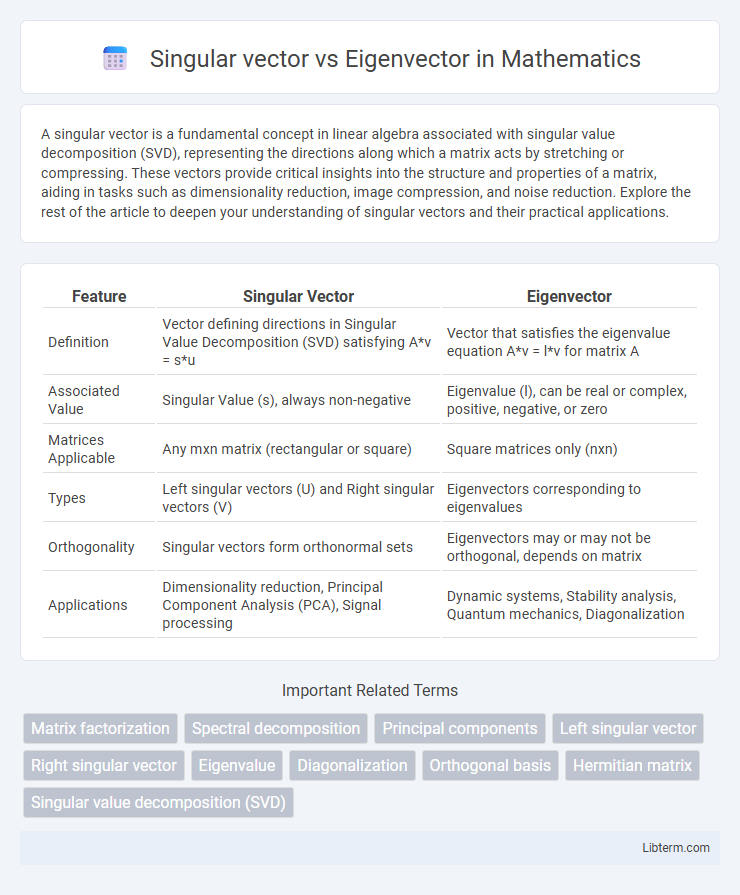
| Feature | Singular Vector | Eigenvector |
|---|---|---|
| Definition | Vector defining directions in Singular Value Decomposition (SVD) satisfying A*v = s*u | Vector that satisfies the eigenvalue equation A*v = l*v for matrix A |
| Associated Value | Singular Value (s), always non-negative | Eigenvalue (l), can be real or complex, positive, negative, or zero |
| Matrices Applicable | Any mxn matrix (rectangular or square) | Square matrices only (nxn) |
| Types | Left singular vectors (U) and Right singular vectors (V) | Eigenvectors corresponding to eigenvalues |
| Orthogonality | Singular vectors form orthonormal sets | Eigenvectors may or may not be orthogonal, depends on matrix |
| Applications | Dimensionality reduction, Principal Component Analysis (PCA), Signal processing | Dynamic systems, Stability analysis, Quantum mechanics, Diagonalization |
Introduction to Singular Vectors and Eigenvectors
Singular vectors and eigenvectors are fundamental concepts in linear algebra used to analyze matrices. Eigenvectors correspond to a square matrix and represent directions where linear transformations scale by corresponding eigenvalues. Singular vectors arise from the singular value decomposition (SVD) of any rectangular matrix, revealing orthogonal directions associated with singular values that capture the matrix's intrinsic geometric features.
Definitions: Singular Vector vs Eigenvector
Singular vectors arise from the Singular Value Decomposition (SVD) of a matrix, representing the directions along which a matrix acts by scaling with singular values. Eigenvectors are vectors associated with a square matrix that, when multiplied by the matrix, yield a scalar multiple of themselves defined by eigenvalues. While eigenvectors require a square matrix and relate to linear transformations, singular vectors apply to any m-by-n matrix, capturing both left and right invariant directions.
Mathematical Foundations: SVD and Eigen Decomposition
Singular Value Decomposition (SVD) generalizes eigen decomposition by factoring any \( m \times n \) matrix \( A \) into \( U \Sigma V^T \), where \( U \) and \( V \) contain orthonormal singular vectors and \( \Sigma \) holds singular values representing the matrix's scaling effects. Eigen decomposition applies specifically to square matrices \( A \), expressing them as \( Q \Lambda Q^{-1} \), where \( Q \) contains eigenvectors and \( \Lambda \) is a diagonal matrix of eigenvalues that signify invariant directions under linear transformation. While eigenvectors solve \( A \mathbf{x} = \lambda \mathbf{x} \), singular vectors satisfy \( A \mathbf{v} = \sigma \mathbf{u} \) and \( A^T \mathbf{u} = \sigma \mathbf{v} \), highlighting their roles in transforming domain and codomain with non-square matrices.
Key Differences Between Singular Vectors and Eigenvectors
Singular vectors arise from the Singular Value Decomposition (SVD) of a matrix, while eigenvectors come from solving the characteristic equation of a square matrix. Singular vectors exist for any m-by-n matrix and are associated with singular values, whereas eigenvectors exist only for square matrices and correspond to eigenvalues. Singular vectors provide an orthonormal basis for both the column and row spaces, unlike eigenvectors which typically correspond to a single space.
Similarities and Overlaps
Singular vectors and eigenvectors both represent fundamental directions associated with linear transformations, revealing intrinsic geometric properties of matrices. Both are computed from matrix decompositions--singular vectors from singular value decomposition (SVD) and eigenvectors from eigenvalue decomposition (EVD)--and often coincide when dealing with symmetric positive semidefinite matrices. They share the essential role of defining invariant subspaces, with singular vectors extending the concept of eigenvectors to all matrices, including non-square and non-symmetric cases.
Applications of Singular Vectors
Singular vectors, derived from Singular Value Decomposition (SVD), play a crucial role in applications such as Principal Component Analysis (PCA) for dimensionality reduction, noise reduction in signal processing, and latent semantic analysis in natural language processing. Unlike eigenvectors, which are defined for square matrices, singular vectors apply to any rectangular matrix, enabling broader use in data compression, image recognition, and collaborative filtering in recommendation systems. Their capacity to reveal inherent structure in data matrices makes them fundamental for extracting meaningful features in machine learning and computer vision tasks.
Applications of Eigenvectors
Eigenvectors play a crucial role in various applications such as principal component analysis (PCA) for dimensionality reduction, stability analysis in differential equations, and vibration analysis in mechanical systems. In contrast to singular vectors from singular value decomposition (SVD), eigenvectors are specifically used to identify invariant directions under linear transformations, enabling feature extraction and system behavior understanding. Their ability to reveal intrinsic properties of matrices makes eigenvectors essential in fields like machine learning, physics, and engineering.
Geometric Interpretation
Singular vectors of a matrix represent directions along which the transformation scales input vectors by singular values, mapping the unit sphere to an ellipsoid with axes defined by these vectors. Eigenvectors describe directions that remain invariant under a linear transformation, scaling only by the corresponding eigenvalues without changing direction. Geometrically, singular vectors characterize the input and output orientations of the matrix in terms of stretch and compression, while eigenvectors identify intrinsic directions of linear transformation preserving vector orientation.
Computational Considerations
Singular vectors in Singular Value Decomposition (SVD) are computed for rectangular matrices, making them suitable for applications involving non-square data, while eigenvectors arise from square matrices in Eigenvalue Decomposition (EVD). The computational complexity of SVD is generally higher, with typical algorithms running in O(mn^2) for an m-by-n matrix, compared to the O(n^3) complexity for EVD of an n-by-n matrix. Numerical stability favors SVD for ill-conditioned or non-symmetric matrices, whereas EVD is more efficient and sufficient for symmetric positive definite matrices.
Summary: Choosing Between Singular Vectors and Eigenvectors
Singular vectors provide orthogonal bases for both row and column spaces in any matrix, making them essential in singular value decomposition (SVD) for handling non-square or non-symmetric matrices. Eigenvectors arise from square matrices and are key in eigenvalue decomposition, revealing intrinsic properties related to the matrix's characteristic polynomial. When selecting between singular vectors and eigenvectors, prioritize singular vectors for general matrix analysis and dimensionality reduction, while eigenvectors excel in applications involving symmetric matrices and stability analysis.
Singular vector Infographic
 libterm.com
libterm.com