Branch value determines the importance and performance of a specific branch within a company or organization, directly influencing profit margins and customer satisfaction. Understanding your branch value helps optimize operations, allocate resources effectively, and develop targeted growth strategies. Discover more about how assessing branch value can enhance your business outcomes in the following article.
Table of Comparison
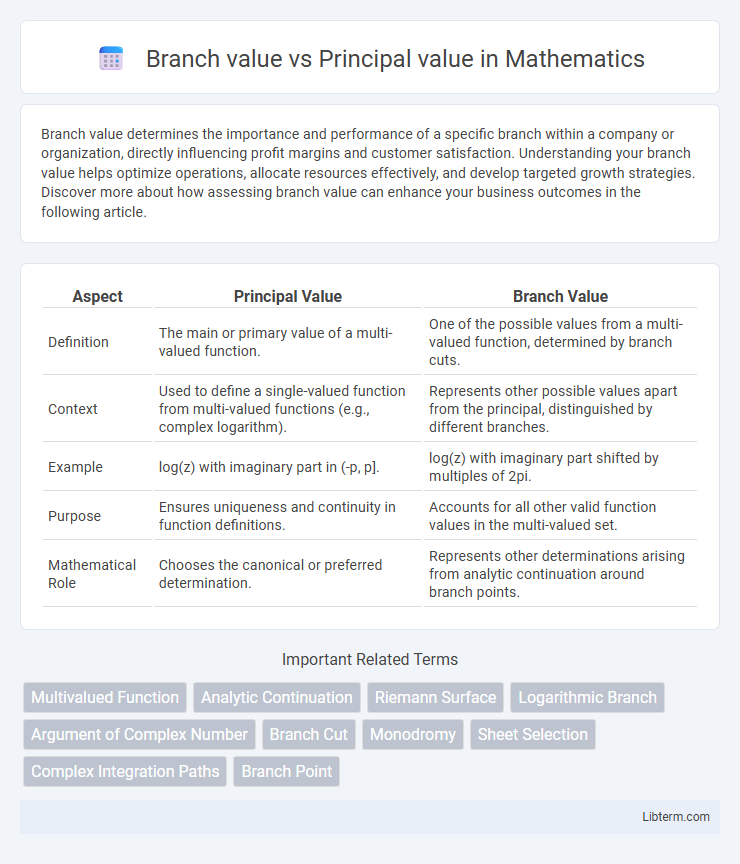
| Aspect | Principal Value | Branch Value |
|---|---|---|
| Definition | The main or primary value of a multi-valued function. | One of the possible values from a multi-valued function, determined by branch cuts. |
| Context | Used to define a single-valued function from multi-valued functions (e.g., complex logarithm). | Represents other possible values apart from the principal, distinguished by different branches. |
| Example | log(z) with imaginary part in (-p, p]. | log(z) with imaginary part shifted by multiples of 2pi. |
| Purpose | Ensures uniqueness and continuity in function definitions. | Accounts for all other valid function values in the multi-valued set. |
| Mathematical Role | Chooses the canonical or preferred determination. | Represents other determinations arising from analytic continuation around branch points. |
Introduction to Branch Value and Principal Value
Branch value represents the current worth of potential future cash flows from a specific business segment, reflecting its profitability and growth prospects. Principal value refers to the original amount invested or loaned, which remains fixed and does not account for changes in market conditions or performance. Understanding the distinction between branch value and principal value is essential for evaluating investment returns and financial health in corporate finance.
Mathematical Definitions: Branch Value vs Principal Value
Branch value and principal value are concepts in complex analysis related to multi-valued functions such as logarithms and roots. The principal value is a specific single-valued branch of a multi-valued function, often defined by restricting the argument to a principal branch cut to ensure uniqueness. Branch values represent different values of the function obtained by continuing along various paths around branch points, reflecting the function's multi-valued nature.
Significance in Complex Analysis
Branch value and principal value play crucial roles in complex analysis for understanding multi-valued functions like logarithms and complex powers. The principal value provides a single, well-defined outcome by restricting the argument to a primary branch, ensuring consistency in calculations. Branch values capture the function's multiple possible outputs across different branches, revealing the function's full analytic structure and behavior near branch cuts and singularities.
Principal Value in Real and Complex Integrals
Principal value plays a crucial role in evaluating real and complex integrals by handling singularities and ensuring convergence where classical integrals diverge. It provides a method to assign finite values to integrals with improper points through symmetric limits, distinguishing it from the branch value associated with multi-valued functions and branch cuts. In complex analysis, the Cauchy principal value extends integration techniques to deal with pole singularities on the real axis, facilitating the rigorous treatment of integrals in contour integration and distribution theory.
Branch Values in Multi-Valued Functions
Branch values in multi-valued functions represent distinct function outputs arising from different branches of a complex function, such as roots or logarithms, at a given point. These branch values help characterize the local behavior of functions on Riemann surfaces, where each branch corresponds to a unique analytic continuation. Understanding branch values is crucial for analyzing discontinuities and multi-valuedness in complex analysis, distinguishing them from the principal value, which typically refers to a single, canonical selection among branches.
Calculating Principal Values: Methods and Examples
Calculating principal values involves determining the main or largest values in a dataset or function, often used in engineering and physics for stress analysis or signal processing. Common methods include eigenvalue decomposition, where matrices are analyzed to extract principal values representing magnitude and direction, and numerical techniques such as the power iteration method, which approximates dominant eigenvalues efficiently. For example, in structural engineering, the principal stress values are calculated by solving the characteristic equation of the stress tensor matrix, yielding key insights into material behavior under load.
Handling Branch Cuts and Branch Points
Branch value and principal value concepts are critical in handling multi-valued complex functions, especially regarding branch cuts and branch points. The principal value defines the standard determination of a multi-valued function, typically restricting the argument of complex numbers to a principal interval, while branch values represent alternative function values obtained by analytically continuing around branch points. Managing branch cuts involves selecting curves in the complex plane to limit the function to a single-valued branch, ensuring continuity and avoiding ambiguity in evaluations near branch points where the function behavior changes discontinuously.
Common Applications in Physics and Engineering
Branch value and principal value frequently arise in complex analysis, integral calculus, and signal processing within physics and engineering. Principal value helps evaluate integrals with singularities, essential in electromagnetic theory and fluid dynamics for solving boundary value problems. Branch values are crucial in quantum mechanics and acoustics when dealing with multivalued functions like complex logarithms and complex power functions to ensure consistent phase and amplitude interpretations.
Challenges and Pitfalls in Selecting Branches
Selecting branches involves challenges such as accurately estimating branch value, which depends on future cash flows and market conditions, unlike principal value that reflects the original investment cost. Misjudging branch value can lead to overvaluation or undervaluation risks, impacting resource allocation and strategic decisions. Pitfalls include ignoring branch-specific risks, failing to account for local market dynamics, and over-reliance on historical data that may not predict future performance.
Summary: Choosing Between Branch Value and Principal Value
Choosing between branch value and principal value depends on the specific goals of investment or accounting assessments. Branch value reflects the worth of a particular subsidiary or division within a company, useful for localized performance evaluation and strategic decisions. Principal value represents the core amount of an investment or loan, emphasizing the fundamental financial commitment and overall asset valuation.
Branch value Infographic
 libterm.com
libterm.com