Euclidean geometry focuses on the study of flat spaces based on points, lines, and planes following Euclid's postulates, which have been foundational in mathematics and engineering. It contrasts with non-Euclidean geometries that explore curved spaces and alternative postulate systems. Discover how Euclidean principles shape your understanding of space and their applications by reading the rest of this article.
Table of Comparison
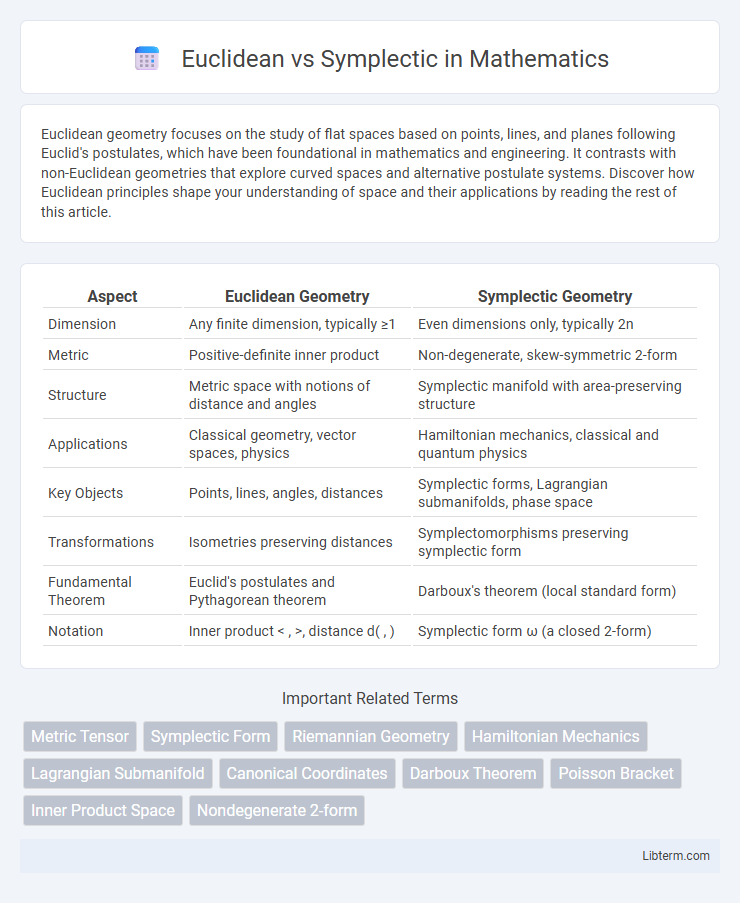
| Aspect | Euclidean Geometry | Symplectic Geometry |
|---|---|---|
| Dimension | Any finite dimension, typically ≥1 | Even dimensions only, typically 2n |
| Metric | Positive-definite inner product | Non-degenerate, skew-symmetric 2-form |
| Structure | Metric space with notions of distance and angles | Symplectic manifold with area-preserving structure |
| Applications | Classical geometry, vector spaces, physics | Hamiltonian mechanics, classical and quantum physics |
| Key Objects | Points, lines, angles, distances | Symplectic forms, Lagrangian submanifolds, phase space |
| Transformations | Isometries preserving distances | Symplectomorphisms preserving symplectic form |
| Fundamental Theorem | Euclid's postulates and Pythagorean theorem | Darboux's theorem (local standard form) |
| Notation | Inner product < , >, distance d( , ) | Symplectic form ω (a closed 2-form) |
Introduction to Geometric Structures
Euclidean and symplectic geometries represent fundamental geometric structures with distinct properties and applications in mathematics and physics. Euclidean geometry centers on concepts of distance and angles within flat spaces, governed by the Euclidean metric, while symplectic geometry studies smooth manifolds equipped with a closed, non-degenerate 2-form known as the symplectic form, crucial in classical mechanics and Hamiltonian systems. Understanding these geometric structures provides essential insights into topology, differential geometry, and mathematical physics, distinguishing metric-based frameworks from those based on symplectic invariants.
Defining the Euclidean Geometry
Euclidean geometry is defined by the study of flat, two-dimensional planes governed by the axioms established by Euclid, emphasizing properties of points, lines, angles, and shapes such as triangles and circles. It relies on the parallel postulate, where parallel lines never intersect, and distances and angles are preserved under rigid transformations like rotations and translations. Distinct from symplectic geometry, Euclidean geometry primarily tackles metric concepts, enabling precise measurement of lengths and angles in a flat, uniform space.
Understanding Symplectic Geometry
Symplectic geometry studies manifolds equipped with a closed, non-degenerate 2-form called the symplectic form, contrasting Euclidean geometry's focus on distances and angles via the inner product. Symplectic spaces are even-dimensional and lack a natural notion of length, emphasizing properties invariant under symplectomorphisms, crucial for understanding Hamiltonian dynamics. This framework underpins classical mechanics by encoding phase space structures, providing a geometric foundation beyond the metric-centric Euclidean setup.
Key Differences Between Euclidean and Symplectic Spaces
Euclidean spaces are characterized by a positive-definite inner product that defines distances and angles, enabling traditional geometric interpretations such as length and orthogonality. Symplectic spaces, in contrast, are equipped with a non-degenerate, skew-symmetric bilinear form called the symplectic form, which does not measure lengths but encodes area-preserving transformations crucial in Hamiltonian mechanics. Unlike Euclidean geometry, symplectic geometry lacks a notion of angle or length, emphasizing structures invariant under symplectomorphisms rather than isometries.
Mathematical Foundations and Properties
Euclidean geometry is based on flat, rigid spaces characterized by the Euclidean metric, preserving distances and angles, with foundational elements such as points, lines, and planes satisfying the parallel postulate. Symplectic geometry, rooted in Hamiltonian mechanics, studies smooth, even-dimensional manifolds equipped with a closed, non-degenerate 2-form called the symplectic form, which provides a framework for phase space analysis and conservation laws. Unlike Euclidean spaces, symplectic manifolds do not possess a natural notion of distance or angle but emphasize area preservation and structure-preserving transformations known as symplectomorphisms.
Applications of Euclidean Geometry
Euclidean geometry, characterized by flat space and standard distance measures, serves as the foundation for applications in computer graphics, architectural design, and robotics, where precise measurements and object modeling are essential. It facilitates the creation of algorithms for collision detection, shape recognition, and trajectory planning by relying on well-defined notions of angles, lengths, and parallelism. In contrast, symplectic geometry, rooted in phase space and preserving area during transformations, primarily addresses problems in classical mechanics and Hamiltonian systems.
Real-World Uses of Symplectic Geometry
Symplectic geometry plays a crucial role in classical and quantum mechanics, where it provides the mathematical framework for phase space analysis and Hamiltonian dynamics, outperforming Euclidean geometry in modeling systems with conserved quantities. Applications extend to optics, where symplectic transformations describe light propagation, and control theory, where they underpin stability and controllability of dynamical systems. Real-world uses also include robotic motion planning and celestial mechanics, leveraging symplectic structures to preserve volume and energy over time.
Historical Development and Significance
Euclidean geometry, rooted in the axioms formulated by the ancient Greek mathematician Euclid around 300 BCE, laid the foundational framework for classical geometry by formalizing concepts of points, lines, and planes in a flat, two-dimensional space. Symplectic geometry emerged in the 20th century, deeply connected to the study of Hamiltonian mechanics and the mathematical description of phase spaces in classical physics, emphasizing structures that preserve the symplectic form, a non-degenerate, closed 2-form. The historical development of Euclidean geometry influenced the evolution of mathematical rigor and education, while symplectic geometry's significance lies in its crucial role in modern theoretical physics and advanced studies in dynamical systems.
Challenges in Transitioning Between Euclidean and Symplectic Frameworks
Transitioning between Euclidean and Symplectic frameworks presents significant challenges, primarily due to their fundamentally different geometric structures: Euclidean frameworks rely on metric spaces with distance and angle preservation, while Symplectic frameworks emphasize structures preserving area and phase space volume without a metric. This disparity complicates the formulation of algorithms and computations, as symplectic integrators must maintain invariants like the symplectic form, which is nontrivial when starting from Euclidean interpretations. Furthermore, adapting physical models or numerical methods requires careful handling of coordinate transformations and preserving underlying symplectic geometry, often demanding advanced mathematical tools such as canonical transformations and Hamiltonian mechanics.
Future Directions and Research Trends
Future directions in Euclidean and symplectic geometry emphasize their integration in quantum computing and advanced robotics, where Euclidean metrics optimize spatial analysis and symplectic structures govern dynamic systems. Research trends reveal growing interest in symplectic topology's applications to Hamiltonian mechanics, bridging gaps in understanding phase space geometry and energy conservation. Emerging studies also focus on hybrid computational algorithms combining Euclidean geometry's metric properties with symplectic invariants for enhancing machine learning models in physics-informed contexts.
Euclidean Infographic
 libterm.com
libterm.com