Pseudo-Riemannian geometry extends classical Riemannian geometry by allowing metrics with indefinite signature, enabling the study of spaces where distances can be negative or zero. This generalization is fundamental in the theory of relativity, where spacetime is modeled as a four-dimensional pseudo-Riemannian manifold. Explore the rest of the article to deepen your understanding of pseudo-Riemannian structures and their applications.
Table of Comparison
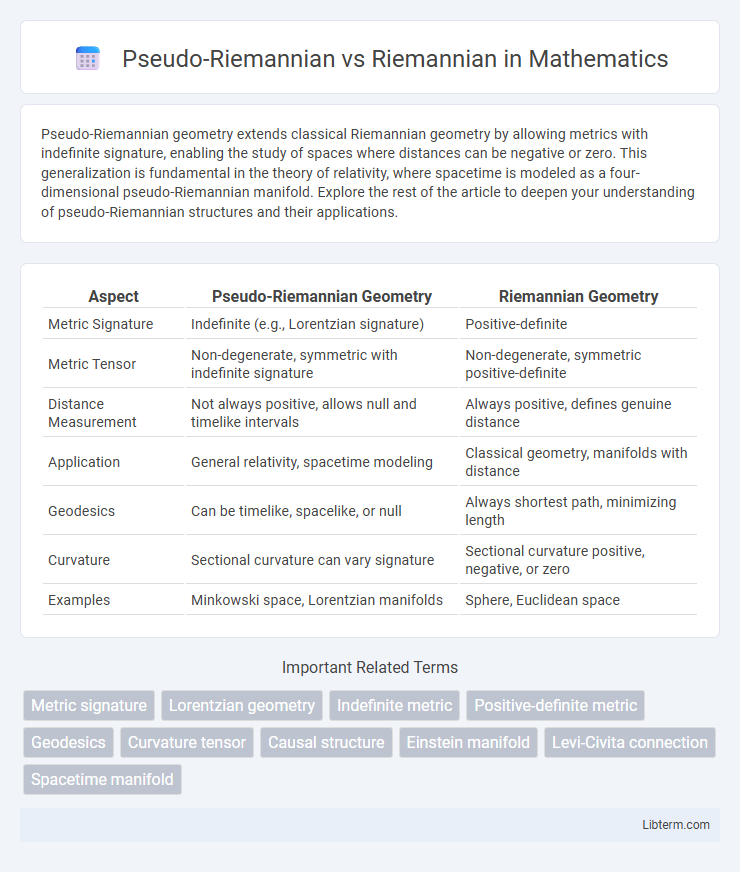
| Aspect | Pseudo-Riemannian Geometry | Riemannian Geometry |
|---|---|---|
| Metric Signature | Indefinite (e.g., Lorentzian signature) | Positive-definite |
| Metric Tensor | Non-degenerate, symmetric with indefinite signature | Non-degenerate, symmetric positive-definite |
| Distance Measurement | Not always positive, allows null and timelike intervals | Always positive, defines genuine distance |
| Application | General relativity, spacetime modeling | Classical geometry, manifolds with distance |
| Geodesics | Can be timelike, spacelike, or null | Always shortest path, minimizing length |
| Curvature | Sectional curvature can vary signature | Sectional curvature positive, negative, or zero |
| Examples | Minkowski space, Lorentzian manifolds | Sphere, Euclidean space |
Introduction to Metric Spaces
Riemannian metrics define positive-definite inner products on tangent spaces, enabling the study of distances and angles in smoothly curved metric spaces essential for classical geometry. Pseudo-Riemannian metrics extend this framework by allowing indefinite inner products, which accommodate models of spacetime in general relativity where time and space dimensions have differing metric signatures. Both structures form the foundation of metric spaces by generalizing notions of length and curvature to complex geometries with varied metric signatures.
Defining Riemannian Manifolds
Riemannian manifolds are smooth manifolds equipped with a positive-definite metric tensor, enabling the measurement of angles and distances in a manner analogous to Euclidean space. In contrast, pseudo-Riemannian manifolds feature a metric tensor with indefinite signature, allowing for the inclusion of time-like dimensions crucial in general relativity. The positive-definite nature of Riemannian metrics ensures all tangent vectors have strictly positive lengths, which is foundational for defining notions such as geodesics, curvature, and volume.
Understanding Pseudo-Riemannian Geometry
Pseudo-Riemannian geometry generalizes Riemannian geometry by allowing the metric tensor to have an indefinite signature, enabling the study of manifolds with both time-like and space-like dimensions, crucial in general relativity. Unlike Riemannian metrics that are positive-definite and measure lengths with strictly positive values, pseudoriemannian metrics accommodate intervals with zero or negative norm squares, reflecting causality structures in spacetime models. Understanding pseudo-Riemannian geometry involves analyzing curvature, geodesics, and topological properties under these generalized metrics, which provide the mathematical foundation for Einstein's field equations.
Key Differences in Metric Signatures
Pseudo-Riemannian manifolds feature metrics with indefinite signatures, allowing for both positive and negative eigenvalues, which enable the description of spacetime in general relativity. In contrast, Riemannian manifolds have positive-definite metric signatures, ensuring all eigenvalues are positive and thus measurements of length are always positive. This fundamental difference in metric signatures dictates their applications: Riemannian geometry models purely spatial structures, while pseudo-Riemannian geometry accommodates the causal structure of spacetime by incorporating time-like dimensions.
Examples in Mathematics and Physics
Pseudo-Riemannian manifolds generalize Riemannian manifolds by allowing indefinite metric signatures, essential in describing spacetime in General Relativity where the Lorentzian metric models gravity and time. Riemannian manifolds, characterized by positive-definite metrics, underpin classical geometry and optimization, seen in the study of curved surfaces like spheres in differential geometry. Examples in physics include the Minkowski space as a pseudo-Riemannian example, while the Euclidean space exemplifies a Riemannian setting influencing fields such as thermodynamics and classical mechanics.
Geodesics in Riemannian and Pseudo-Riemannian Contexts
Geodesics in Riemannian geometry represent the shortest paths between points on a manifold equipped with a positive-definite metric, ensuring all tangent vectors have positive length squares. In contrast, geodesics in Pseudo-Riemannian geometry, such as in Lorentzian manifolds used in general relativity, include timelike, spacelike, and null (lightlike) paths due to the indefinite metric signature, leading to richer causal structures. The distinction between positive-definite and indefinite metrics fundamentally alters geodesic behavior, influencing curvature, length minimization, and physical interpretations.
Curvature: Comparative Properties and Implications
Pseudo-Riemannian manifolds generalize Riemannian manifolds by allowing indefinite metrics, leading to curvature tensors that can exhibit mixed signature effects, unlike the strictly positive-definite curvature in Riemannian geometry. This distinction affects geodesic behavior, with pseudo-Riemannian spaces accommodating null geodesics crucial in general relativity, while Riemannian curvature typically ensures positive sectional curvature properties. The differing curvature invariants impact physical interpretations and the mathematical classification of manifolds, especially in contexts involving Lorentzian metrics and gravitational fields.
Applications: From General Relativity to Pure Geometry
Pseudo-Riemannian geometry underpins General Relativity by modeling spacetime with indefinite metric signatures, allowing the description of gravitational fields and causal structures. Riemannian geometry, characterized by positive-definite metrics, plays a crucial role in pure geometry, providing tools for studying curvature, topology, and geometric analysis on manifolds. Applications of Pseudo-Riemannian metrics extend to theoretical physics and cosmology, whereas Riemannian metrics are foundational in mathematical fields such as differential geometry and global analysis.
Challenges in Transitioning Between Structures
Transitioning from Riemannian to Pseudo-Riemannian geometry involves challenges such as handling indefinite metric signatures, which complicate notions of distance and angle. The lack of positive-definiteness in Pseudo-Riemannian manifolds affects curvature conditions and geodesic behavior, requiring adjusted analytical and topological tools. These complexities impact fields like general relativity, where Lorentzian metrics replace Riemannian structures to model spacetime accurately.
Conclusion: Choosing the Right Framework
Choosing between Pseudo-Riemannian and Riemannian geometry depends on the specific application and underlying metric signature required. Pseudo-Riemannian geometry is essential for modeling spacetime in general relativity due to its indefinite metric, while Riemannian geometry is suited for contexts requiring positive-definite metrics, such as in classical differential geometry and many optimization problems. Understanding the metric signature and its implications on curvature and geodesics is crucial to selecting the appropriate geometric framework.
Pseudo-Riemannian Infographic
 libterm.com
libterm.com