A terminal object is a concept in category theory representing an object with a unique morphism from every other object in the category, ensuring minimal complexity and universal mapping properties. It serves as a foundational element to understand limits and universal constructions across mathematical structures. Explore the rest of the article to uncover how terminal objects influence various fields and your deeper comprehension of abstract mathematics.
Table of Comparison
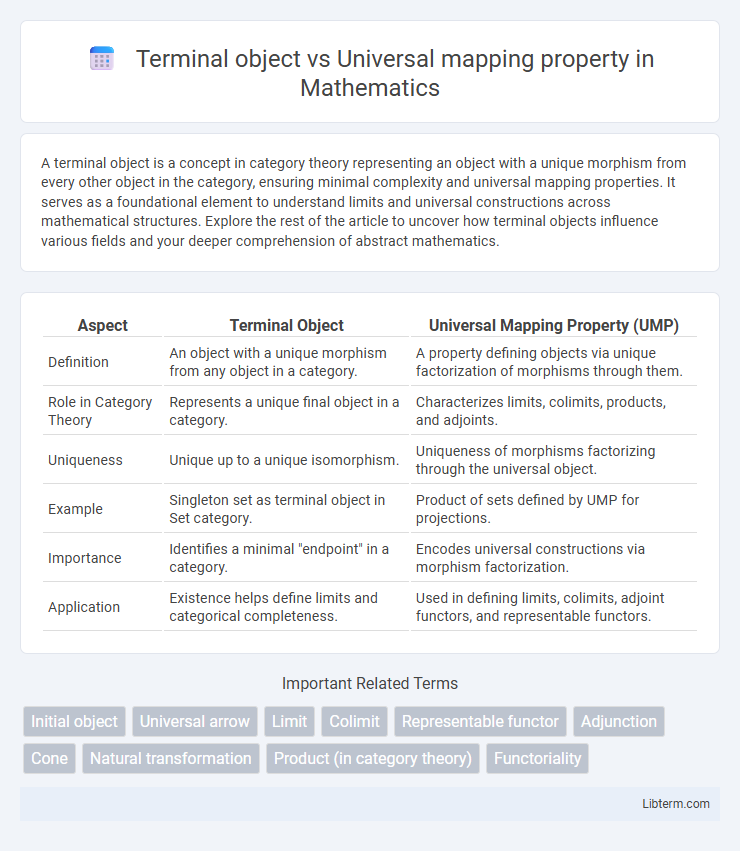
| Aspect | Terminal Object | Universal Mapping Property (UMP) |
|---|---|---|
| Definition | An object with a unique morphism from any object in a category. | A property defining objects via unique factorization of morphisms through them. |
| Role in Category Theory | Represents a unique final object in a category. | Characterizes limits, colimits, products, and adjoints. |
| Uniqueness | Unique up to a unique isomorphism. | Uniqueness of morphisms factorizing through the universal object. |
| Example | Singleton set as terminal object in Set category. | Product of sets defined by UMP for projections. |
| Importance | Identifies a minimal "endpoint" in a category. | Encodes universal constructions via morphism factorization. |
| Application | Existence helps define limits and categorical completeness. | Used in defining limits, colimits, adjoint functors, and representable functors. |
Introduction to Terminal Objects
Terminal objects in category theory represent unique objects with a single morphism from any other object, serving as a foundational concept in understanding universal constructions. They simplify complex structures by providing a universal target, ensuring the existence of a unique morphism that respects the category's composition rules. This concept is crucial for defining limits, adjoints, and other universal mapping properties that underpin advanced mathematical frameworks.
Understanding Universal Mapping Property
The Universal Mapping Property (UMP) characterizes objects in a category by specifying a unique morphism factorization that satisfies a given diagram, enabling the construction of universal solutions to mathematical problems. Terminal objects exemplify UMP by serving as unique targets for morphisms from any object, defining a universal terminal cone in a category. Understanding UMP involves recognizing how it formalizes existence and uniqueness conditions that make constructions like limits, colimits, and representable functors canonical and well-defined.
Definitions and Key Concepts
A terminal object in category theory is an object such that there exists a unique morphism from any other object in the category to this terminal object, representing a universal sink. The universal mapping property characterizes an object by the existence and uniqueness of morphisms related to a specific diagram, defining objects like limits, colimits, and free constructions. Terminal objects are examples of universal mapping properties where the property ensures a unique mapping to the terminal object, illustrating universality and uniqueness in categorical structures.
Terminal Object: Formal Properties
A terminal object in a category is an object T such that for every object X there exists a unique morphism from X to T, ensuring its uniqueness up to isomorphism. The terminal object satisfies the universal mapping property by serving as a universal recipient of morphisms from all objects, enabling commutative diagrams to factor uniquely through it. Its formal properties guarantee existence and uniqueness of such morphisms, making it a fundamental construct in category theory for defining limits and universal cones.
Universal Mapping Property: Formal Framework
The Universal Mapping Property (UMP) provides a formal framework that characterizes an object uniquely up to isomorphism by specifying a universal morphism to or from that object within a category. It defines a natural bijection between morphisms originating or terminating at the universal object and a corresponding set of morphisms from or to other objects, ensuring uniqueness and existence of factorizations. This framework is fundamental in category theory, enabling precise constructions such as limits, colimits, and adjoint functors through universal properties.
Illustrative Examples in Category Theory
The terminal object in category theory is a unique object T such that for every object X, there exists a unique morphism from X to T, exemplified by the singleton set in the category of sets. The universal mapping property characterizes objects like products as an object P along with projection morphisms, ensuring any object with morphisms into the factors uniquely factors through P; for example, the Cartesian product A x B equipped with natural projections satisfies this property. These illustrative examples demonstrate how universal constructions unify diverse mathematical structures via categorical abstractions.
Relationship Between Terminal Objects and Universal Mapping Properties
Terminal objects serve as unique targets in a category, embodying the universal mapping property by providing a single morphism from any object. This relationship highlights that terminal objects represent limit constructions characterized by universal arrows, ensuring uniqueness in factorization. Consequently, terminal objects exemplify universal mapping properties by establishing canonical and natural maps from every object within the category.
Applications in Mathematics and Computer Science
Terminal objects serve as unique universal solutions in categories, enabling the definition of limits and colimits that structure mathematical objects and computations. The universal mapping property characterizes these objects by ensuring unique morphisms from any object, crucial for defining initial algebras and final coalgebras in category theory. In computer science, these concepts underpin type theory, functional programming semantics, and database schema design by formalizing constructions such as products, coproducts, and recursive data types.
Differences and Similarities Explained
Terminal objects and universal mapping properties both characterize objects in a category through unique morphisms. A terminal object is defined by its property that there exists a unique morphism from any object in the category to it, representing a special case of universal mapping property. The universal mapping property generalizes this concept by specifying objects as solutions to particular universality conditions, often involving unique factorization of morphisms, which makes terminal objects a specific instance within this broader framework.
Summary and Further Reading
A terminal object in category theory is an object with a unique morphism from every other object, embodying the concept of a universal construction. The universal mapping property characterizes constructions like products or limits by defining objects through unique morphisms satisfying specific conditions. For further reading, explore standard texts such as "Categories for the Working Mathematician" by Saunders Mac Lane and "Category Theory" by Steve Awodey, which provide in-depth explanations and examples of these foundational concepts.
Terminal object Infographic
 libterm.com
libterm.com