Quaternions are a number system that extends complex numbers, widely used in 3D computer graphics and robotics for representing rotations without suffering from gimbal lock. They consist of one real part and three imaginary parts, enabling smooth interpolation and efficient computations in spatial transformations. Explore the rest of this article to understand how quaternions can enhance your work with 3D rotations and spatial mathematics.
Table of Comparison
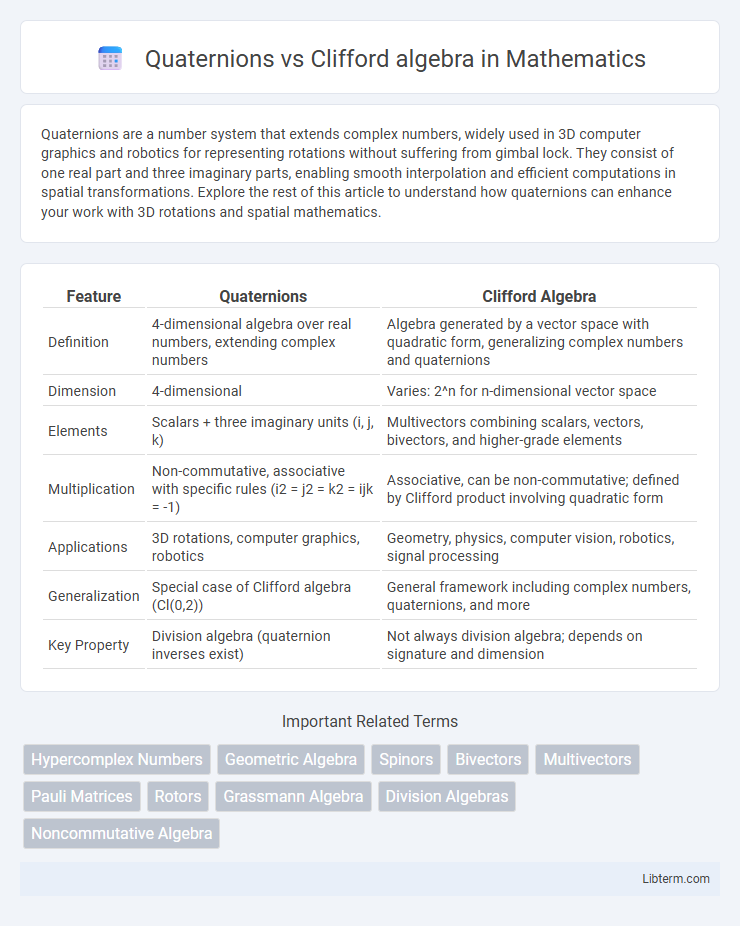
| Feature | Quaternions | Clifford Algebra |
|---|---|---|
| Definition | 4-dimensional algebra over real numbers, extending complex numbers | Algebra generated by a vector space with quadratic form, generalizing complex numbers and quaternions |
| Dimension | 4-dimensional | Varies: 2^n for n-dimensional vector space |
| Elements | Scalars + three imaginary units (i, j, k) | Multivectors combining scalars, vectors, bivectors, and higher-grade elements |
| Multiplication | Non-commutative, associative with specific rules (i2 = j2 = k2 = ijk = -1) | Associative, can be non-commutative; defined by Clifford product involving quadratic form |
| Applications | 3D rotations, computer graphics, robotics | Geometry, physics, computer vision, robotics, signal processing |
| Generalization | Special case of Clifford algebra (Cl(0,2)) | General framework including complex numbers, quaternions, and more |
| Key Property | Division algebra (quaternion inverses exist) | Not always division algebra; depends on signature and dimension |
Introduction to Quaternions and Clifford Algebra
Quaternions, first described by William Rowan Hamilton in 1843, form a four-dimensional non-commutative division algebra extending complex numbers, widely used in 3D rotation and computer graphics. Clifford algebras generalize quaternions by encompassing multivector spaces with geometric interpretations, playing a key role in physics, robotics, and computer vision for representing rotations and reflections in higher dimensions. Both structures serve as fundamental tools for encoding geometric transformations, with Clifford algebra offering a more comprehensive framework that includes quaternions as a special case.
Historical Development and Key Contributors
Quaternions, introduced by William Rowan Hamilton in 1843, pioneered the extension of complex numbers to four dimensions, laying foundational work in algebra and geometry. Clifford algebra, developed later by William Kingdon Clifford building on the ideas of Grassmann and Hamilton, generalized quaternions to support higher-dimensional spaces and geometric transformations. Key contributors such as Elie Cartan further advanced Clifford algebra applications in physics and mathematics, solidifying its role in modern geometric algebra.
Fundamental Mathematical Structures
Quaternions form a four-dimensional normed division algebra over the real numbers, featuring elements composed of one real and three imaginary units with specific multiplication rules that enable rotation representations in three-dimensional space. Clifford algebra generalizes complex numbers, quaternions, and several other algebraic systems through geometric product operations on multivectors, providing a unified framework for describing rotations, reflections, and other transformations in higher-dimensional spaces. The fundamental difference lies in quaternions being a specific algebraic system with fixed dimensionality, whereas Clifford algebras encompass a broad family of associative algebras parameterized by vector spaces and quadratic forms, significantly expanding the scope and applications of geometric computations.
Dimensional Representation and Scalability
Quaternions provide a four-dimensional representation ideal for 3D rotations and spatial transformations, offering computational efficiency in graphics and robotics. Clifford algebra extends this framework to higher dimensions, enabling scalable manipulation of multivectors across arbitrary dimensional spaces, enhancing versatility in physics and computer vision. The scalability of Clifford algebra makes it suitable for complex geometric calculations beyond the fixed dimensionality of quaternions.
Algebraic Operations and Properties
Quaternions form a four-dimensional non-commutative division algebra over the real numbers, primarily used for representing rotations in three-dimensional space with multiplication defined by the Hamilton product. Clifford algebra generalizes quaternions by incorporating multivector elements and a geometric product that combines both the inner and outer products, enabling algebraic operations on vectors of arbitrary dimensions with graded elements. While quaternions maintain associativity and have invertible elements, Clifford algebras exhibit richer algebraic structures, including graded involutions and extensible algebraic frameworks for geometric transformations beyond those achievable by quaternions.
Applications in Physics and Engineering
Quaternions excel in representing three-dimensional rotations and orientations, making them vital in aerospace navigation, robotics, and computer graphics for efficient and stable computations. Clifford algebra generalizes quaternions, facilitating the modeling of complex geometric transformations, electromagnetism, and quantum mechanics by unifying scalars, vectors, and higher-dimensional elements in physics and engineering. Both frameworks enhance the mathematical modeling of spatial phenomena, with Clifford algebra providing a broader toolkit for relativistic physics and multi-dimensional signal processing.
Geometric Interpretations and Transformations
Quaternions represent rotations in three-dimensional space using a four-dimensional algebraic system, efficiently encoding orientation and avoiding gimbal lock. Clifford algebra generalizes this by providing a framework for multivector entities that represent complex geometric transformations, including rotations, reflections, and dilations, in various dimensions. The geometric interpretation in Clifford algebra unifies and extends quaternionic rotations through a richer set of operators that manipulate subspaces and geometric objects beyond angular displacements.
Computational Efficiency and Practical Considerations
Quaternions offer computational efficiency in 3D rotations due to their compact four-dimensional structure, requiring fewer operations for interpolation and avoiding gimbal lock in computer graphics and robotics. Clifford algebra extends this functionality by representing rotations and reflections in higher dimensions but introduces increased computational overhead and complexity in implementation. Practical applications favor quaternions for real-time systems requiring fast and stable rotation computations, while Clifford algebra suits advanced geometric modeling where multidimensional transformations demand more expressive mathematical frameworks.
Limitations and Challenges of Each Approach
Quaternions are limited by their dimensionality, restricting their application primarily to 3D rotations and making them less suitable for higher-dimensional problems encountered in physics and computer graphics. Clifford algebra addresses these dimensional constraints by generalizing quaternions, but it introduces greater computational complexity and a steeper learning curve, which can hinder widespread implementation. Both approaches face challenges in numerical stability and interpretation when applied to intricate geometric transformations or multi-dimensional spaces.
Choosing Between Quaternions and Clifford Algebra
Choosing between Quaternions and Clifford Algebra depends on the complexity and dimensionality of the problem, with Quaternions offering efficient rotation representation in three dimensions while Clifford Algebra extends naturally to higher dimensions and handles multivector calculations. Quaternions are computationally simpler and widely used in 3D graphics, robotics, and aerospace engineering, whereas Clifford Algebra provides a unified framework for geometry, including reflections, rotations, and projections in various dimensions. For applications requiring advanced geometric transformations and algebraic generality beyond 3D rotations, Clifford Algebra is the preferred choice; simpler rotation tasks favor Quaternions for performance and ease of implementation.
Quaternions Infographic
 libterm.com
libterm.com