A nowhere differentiable function is a continuous function that does not have a derivative at any point in its domain, challenging traditional notions of smoothness in calculus. These functions often exhibit highly irregular and fractal-like behavior, making them important in fields such as mathematical analysis and chaos theory. Explore the article to deepen your understanding of nowhere differentiable functions and their remarkable properties.
Table of Comparison
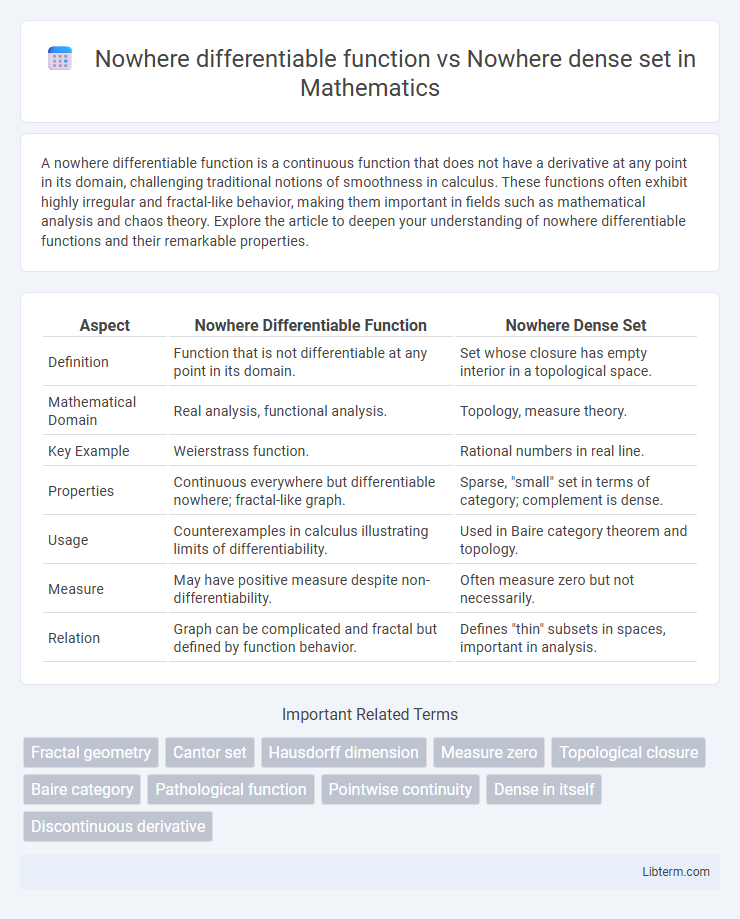
| Aspect | Nowhere Differentiable Function | Nowhere Dense Set |
|---|---|---|
| Definition | Function that is not differentiable at any point in its domain. | Set whose closure has empty interior in a topological space. |
| Mathematical Domain | Real analysis, functional analysis. | Topology, measure theory. |
| Key Example | Weierstrass function. | Rational numbers in real line. |
| Properties | Continuous everywhere but differentiable nowhere; fractal-like graph. | Sparse, "small" set in terms of category; complement is dense. |
| Usage | Counterexamples in calculus illustrating limits of differentiability. | Used in Baire category theorem and topology. |
| Measure | May have positive measure despite non-differentiability. | Often measure zero but not necessarily. |
| Relation | Graph can be complicated and fractal but defined by function behavior. | Defines "thin" subsets in spaces, important in analysis. |
Introduction to Nowhere Differentiable Functions
Nowhere differentiable functions are continuous functions that lack a derivative at every point in their domain, exemplified by the Weierstrass function, which challenges traditional notions of smoothness in calculus. These functions illustrate extreme irregularity and fractal-like behavior, serving as vital counterexamples in real analysis to the assumption that continuity implies differentiability almost everywhere. In contrast, nowhere dense sets are topological concepts describing sets whose closure has an empty interior, fundamentally differing from the analytical nature of nowhere differentiable functions.
Understanding Nowhere Dense Sets
Nowhere dense sets are subsets of a topological space whose closure has empty interior, meaning they are "small" in terms of topological size and contain no open subsets. Unlike nowhere differentiable functions, which are continuous but lack tangent lines at any point, nowhere dense sets are primarily studied within topology to understand the structure and distribution of sets with minimal topological influence. Recognizing nowhere dense sets is crucial in analysis and topology for characterizing meager sets and understanding Baire category theory.
Fundamental Differences: Function vs Set
A nowhere differentiable function is a type of mathematical function characterized by the absence of a well-defined tangent or derivative at every point in its domain, illustrating complex, often fractal-like behavior. In contrast, a nowhere dense set is a concept from topology describing a set whose closure has an empty interior, meaning it is "small" or "thin" in a topological space. The fundamental difference lies in their nature: a nowhere differentiable function involves the complexity of function behavior over an interval, while a nowhere dense set concerns the spatial distribution and topological properties of points within a space.
Historical Context and Key Mathematicians
The concept of a nowhere differentiable function emerged prominently through the work of Karl Weierstrass in 1872, who constructed the first explicit example challenging the traditional notion of smoothness in analysis. Meanwhile, the idea of a nowhere dense set was formalized within the framework of point-set topology by mathematicians like Rene Baire around the turn of the 20th century, particularly through Baire's category theorem in 1899. Both ideas fundamentally influenced modern analysis and topology, shaping understanding of function behavior and set structure beyond classical intuitions.
Mathematical Definitions and Properties
A nowhere differentiable function is a continuous function that lacks a derivative at every point in its domain, commonly exemplified by the Weierstrass function, highlighting its fractal-like complexity and non-smooth behavior. A nowhere dense set in topology is a set whose closure has empty interior, meaning it is "small" in the sense that it does not contain any interval, often used in the study of Baire category theory. Both concepts illustrate extremes in mathematical analysis and topology, where nowhere differentiable functions defy classical smoothness, and nowhere dense sets characterize sparse, topologically insignificant subsets of a space.
Examples of Nowhere Differentiable Functions
Nowhere differentiable functions, such as the classic Weierstrass function and Takagi function, exhibit continuous behavior without possessing a derivative at any point, illustrating pathological cases in real analysis. These functions contrast with nowhere dense sets, which are topological constructs describing sets with empty interiors and no dense presence in any interval. Exploring examples like the Weierstrass function reveals complex fractal structures and emphasizes the subtlety in differentiability compared to the geometric scarcity expressed by nowhere dense sets.
Examples of Nowhere Dense Sets
Examples of nowhere dense sets include the Cantor set, which is a classic fractal with zero Lebesgue measure and no intervals, and the set of rational numbers, which is dense in the real numbers but nowhere dense in itself. Unlike nowhere differentiable functions such as the Weierstrass function, which are continuous everywhere but differentiable nowhere, nowhere dense sets lack any non-empty open intervals, making them sparse within their ambient space. These sets play a crucial role in topology and real analysis by providing counterexamples and illustrating concepts of measure and category.
Topological and Analytical Implications
A nowhere differentiable function, such as the Weierstrass function, exhibits pathological behavior in analysis by lacking a finite derivative at every point, challenging classical smoothness assumptions. In contrast, a nowhere dense set is a topological concept describing sets whose closure has empty interior, highlighting their scarcity or thinness within a space. The analytical implication of nowhere differentiable functions contrasts with the geometric sparseness of nowhere dense sets, bridging intricate properties in analysis and topology relevant to fractals and measure theory.
Applications in Modern Mathematics
Nowhere differentiable functions, such as Weierstrass functions, model irregular phenomena in fractal geometry and stochastic processes, enabling precise analysis in fields like signal processing and chaos theory. Nowhere dense sets play a critical role in topology and functional analysis by characterizing meager sets and residual properties in Banach spaces, which is essential for understanding generic properties and Baire category theorem applications. Both concepts provide foundational tools in modern mathematics for exploring complexity, continuity, and sparsity within various analytical and topological frameworks.
Summary and Comparative Analysis
A nowhere differentiable function is a function that lacks a derivative at every point in its domain, exemplified by functions like the Weierstrass function, which exhibit continuous but highly irregular behavior. In contrast, a nowhere dense set in topology is a set whose closure has empty interior, meaning it is sparse and does not contain any open subset, often encountered in fractal geometry and measure theory. While nowhere differentiable functions characterize extreme irregularity in analysis, nowhere dense sets describe topological thinness, making their comparison essential in understanding pathological objects in mathematical analysis and topology.
Nowhere differentiable function Infographic
 libterm.com
libterm.com