Gaussian measure plays a crucial role in probability theory and functional analysis by assigning probabilities to sets in infinite-dimensional spaces, generalizing the normal distribution. It serves as a foundational concept in areas such as stochastic processes, machine learning, and quantum mechanics, where the behavior of random variables follows a Gaussian distribution. Explore the article to deepen your understanding of Gaussian measure and its applications across various scientific disciplines.
Table of Comparison
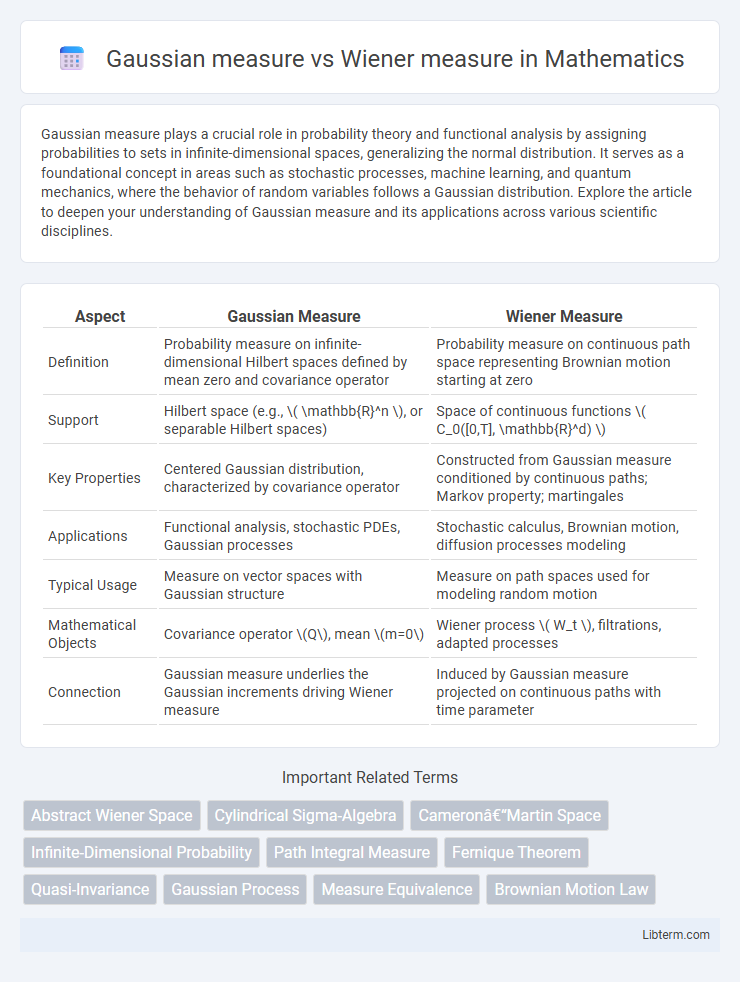
| Aspect | Gaussian Measure | Wiener Measure |
|---|---|---|
| Definition | Probability measure on infinite-dimensional Hilbert spaces defined by mean zero and covariance operator | Probability measure on continuous path space representing Brownian motion starting at zero |
| Support | Hilbert space (e.g., \( \mathbb{R}^n \), or separable Hilbert spaces) | Space of continuous functions \( C_0([0,T], \mathbb{R}^d) \) |
| Key Properties | Centered Gaussian distribution, characterized by covariance operator | Constructed from Gaussian measure conditioned by continuous paths; Markov property; martingales |
| Applications | Functional analysis, stochastic PDEs, Gaussian processes | Stochastic calculus, Brownian motion, diffusion processes modeling |
| Typical Usage | Measure on vector spaces with Gaussian structure | Measure on path spaces used for modeling random motion |
| Mathematical Objects | Covariance operator \(Q\), mean \(m=0\) | Wiener process \( W_t \), filtrations, adapted processes |
| Connection | Gaussian measure underlies the Gaussian increments driving Wiener measure | Induced by Gaussian measure projected on continuous paths with time parameter |
Introduction to Gaussian Measure and Wiener Measure
Gaussian measure is a probability measure on infinite-dimensional spaces that generalizes the concept of the normal distribution to functional settings, characterized by mean zero and covariance operators on Hilbert spaces. Wiener measure specifically describes the probability distribution of Brownian motion paths on the space of continuous functions, serving as a fundamental example of a Gaussian measure with covariance given by the minimum function. Understanding these measures is essential for studying stochastic processes, functional analysis, and applications in fields such as mathematical physics and financial mathematics.
Fundamental Definitions and Concepts
Gaussian measure is a probability measure on finite-dimensional Euclidean spaces characterized by a mean vector and covariance matrix, defining distributions with properties of normality and symmetry. Wiener measure extends Gaussian measure to infinite-dimensional function spaces, specifically on the space of continuous paths, modeling Brownian motion as a fundamental example of a Gaussian process. The core difference lies in dimensionality: Gaussian measure applies to vectors, while Wiener measure describes probability distributions over continuous stochastic processes.
Historical Development and Applications
The Gaussian measure, rooted in probability theory and functional analysis, originated from the study of normal distributions and infinite-dimensional vector spaces, playing a foundational role in statistical mechanics and quantum field theory. The Wiener measure, introduced by Norbert Wiener in the 1920s, formalized the mathematical description of Brownian motion by providing a probability measure on the space of continuous paths, revolutionizing stochastic processes and diffusion modeling. Both measures have critical applications in fields such as financial mathematics, with Gaussian measures underpinning Gaussian processes and Wiener measures used in option pricing models and stochastic calculus.
Mathematical Construction of Gaussian Measure
The Gaussian measure is rigorously constructed through the probability distribution of a multivariate normal vector, characterized by its mean vector and covariance operator in a Hilbert space, often realized via the Minlos theorem or abstract Wiener space framework. This construction involves defining a Gaussian cylindrical measure on a topological vector space and extending it to a complete Borel measure that respects the underlying covariance structure. In contrast, the Wiener measure arises as a Gaussian measure specifically associated with Brownian motion paths on a function space, equipped with a canonical Gaussian covariance corresponding to the Brownian covariance kernel.
Mathematical Construction of Wiener Measure
Wiener measure is constructed as a probability measure on the space of continuous functions, specifically using the limit of finite-dimensional Gaussian distributions corresponding to Brownian motion increments. The measure is defined on the path space C[0,1] with the sigma-algebra generated by cylinder sets, leveraging the Kolmogorov extension theorem to ensure consistency of finite-dimensional distributions. Unlike a Gaussian measure on a finite-dimensional vector space, Wiener measure captures the infinite-dimensional nature of Brownian paths and encodes their temporal dependence structure through covariance given by the minimum function.
Key Differences Between Gaussian and Wiener Measures
Gaussian measure is a probability measure defined on infinite-dimensional Hilbert spaces, characterized by its mean and covariance operator, generally used to describe distributions of Gaussian processes. Wiener measure, a special case of Gaussian measure, specifically models the distribution of Brownian motion paths with zero mean and covariance given by the minimum of two times. Key differences include that Gaussian measure encompasses a broader class of Gaussian processes with various covariance structures, while Wiener measure is uniquely tied to continuous paths starting at zero and strictly models Brownian motion on function spaces.
Similarities and Connections
Gaussian measure and Wiener measure both arise in probability theory as measures on infinite-dimensional spaces, with Gaussian measure defined on Hilbert spaces and Wiener measure characterizing the distribution of Brownian motion paths in continuous function spaces. Both are centered Gaussian processes, where Gaussian measure generalizes finite-dimensional normal distributions, and Wiener measure represents the law of a standard Brownian motion, linking them through their covariance structures and reproducing kernel Hilbert spaces. Their shared properties include infinite divisibility, measure concentration phenomena, and fundamental roles in stochastic analysis, functional integration, and the study of Gaussian processes.
Applications in Probability and Stochastic Processes
Gaussian measure underpins the structure of Gaussian processes, essential for modeling continuous-time stochastic phenomena with stationary increments. Wiener measure provides the rigorous probabilistic framework for Brownian motion, facilitating analysis in path-space and stochastic calculus. Both measures enable the study of diffusion processes, option pricing in financial mathematics, and solutions to stochastic differential equations.
Challenges in Working with Each Measure
Gaussian measure presents challenges in infinite-dimensional spaces due to its dependence on covariance operators and difficulties in characterizing tail behavior and concentration inequalities. Wiener measure, a probability measure on continuous paths, faces complexities in handling pathwise properties, measure equivalence, and the non-trivial topology of function spaces. Both measures require advanced techniques in functional analysis and stochastic calculus to address issues related to singularities, support properties, and integration on infinite-dimensional manifolds.
Conclusion and Future Directions
The Gaussian measure serves as a foundation for defining probability distributions in infinite-dimensional spaces, while the Wiener measure specifically models Brownian motion paths with continuous sample functions. Advancements in stochastic analysis and quantum field theory motivate extending these measures to more complex manifolds and non-Gaussian frameworks. Future research aims to enhance numerical methods for Wiener measure simulation and explore applications in machine learning through Gaussian process approximations.
Gaussian measure Infographic
 libterm.com
libterm.com