Modules are essential building blocks in programming, encapsulating functionality into reusable, organized units that enhance code maintainability and readability. They allow developers to import specific features or functions without cluttering the main program, streamlining development and troubleshooting processes. Discover how using modules can transform your coding efficiency by exploring the rest of this article.
Table of Comparison
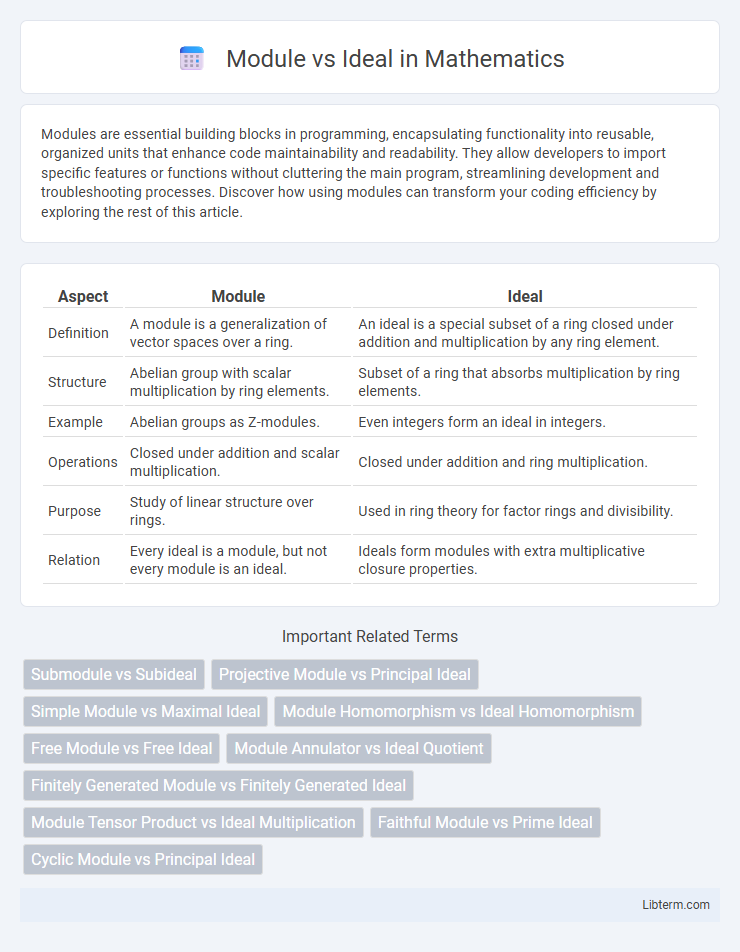
| Aspect | Module | Ideal |
|---|---|---|
| Definition | A module is a generalization of vector spaces over a ring. | An ideal is a special subset of a ring closed under addition and multiplication by any ring element. |
| Structure | Abelian group with scalar multiplication by ring elements. | Subset of a ring that absorbs multiplication by ring elements. |
| Example | Abelian groups as Z-modules. | Even integers form an ideal in integers. |
| Operations | Closed under addition and scalar multiplication. | Closed under addition and ring multiplication. |
| Purpose | Study of linear structure over rings. | Used in ring theory for factor rings and divisibility. |
| Relation | Every ideal is a module, but not every module is an ideal. | Ideals form modules with extra multiplicative closure properties. |
Understanding the Concept: Module vs Ideal
A module is a substructure of a ring that generalizes vector spaces by allowing scalars from rings instead of fields, while an ideal is a special subset of a ring that absorbs multiplication by any ring element and serves as the kernel of ring homomorphisms. Understanding the concept of modules involves studying their structure as abelian groups with compatible ring actions, whereas ideals play a crucial role in constructing quotient rings and defining ring properties such as primality and maximality. Modules extend the idea of linear algebra to ring theory, whereas ideals focus on internal ring subsets important for factorization and algebraic geometry.
Key Definitions in Algebra: Modules and Ideals
Modules generalize vector spaces by allowing scalars from a ring instead of a field, serving as fundamental structures in abstract algebra. Ideals are special subsets of rings that absorb multiplication by ring elements and facilitate the construction of quotient rings. Both concepts play crucial roles in ring theory, with modules broadening the scope of linear algebra and ideals underpinning factorization and ring homomorphisms.
Historical Development: Modules and Ideals in Abstract Algebra
Modules generalize vector spaces by allowing scalar multiplication over a ring instead of a field, evolving from the study of linear algebra structures in the early 20th century. Ideals, originating from ring theory, were introduced by Richard Dedekind and Emmy Noether to generalize number theoretic concepts, serving as crucial tools in factorization and homomorphism analysis. Both concepts shaped modern abstract algebra by providing frameworks for understanding structural properties in rings and modules, influencing developments in algebraic geometry and homological algebra.
Fundamental Properties: Comparing Modules and Ideals
Modules generalize the concept of vector spaces by allowing scalars from rings instead of fields, enabling more flexible algebraic structures, while ideals are special subsets of rings that absorb multiplication by ring elements and play a crucial role in defining quotient rings. A fundamental property of modules is their closure under addition and scalar multiplication, whereas ideals must also be closed under ring multiplication, ensuring absorption properties essential for ring homomorphisms. Comparing modules and ideals highlights that every ideal is a module over its ring, but not every module qualifies as an ideal, emphasizing the structural distinctions based on multiplicative absorption and additive closure.
Structural Differences: Modules vs Ideals
Modules and ideals are fundamental concepts in ring theory with distinct structural differences: a module over a ring generalizes vector spaces by allowing scalars from a ring rather than a field, whereas an ideal is a special subset of a ring that absorbs multiplication by any ring element. Every ideal is inherently a module, but not every module qualifies as an ideal since ideals must be subsets of the ring itself with specific absorption properties. Structurally, modules can have arbitrary elements outside the ring, while ideals are constrained subsets with closure under subtraction and ring multiplication.
Examples of Modules and Ideals in Ring Theory
In ring theory, a module generalizes the concept of vector spaces where scalars come from a ring instead of a field, with examples including abelian groups viewed as modules over the ring of integers. Ideals constitute special subsets of rings that absorb multiplication by ring elements, such as the set of even integers forming an ideal in the ring of all integers. Submodules like the kernel of a module homomorphism illustrate module examples, while principal ideals generated by a single element exemplify ideals critical for constructing quotient rings.
Applications of Ideals and Modules in Mathematics
Modules and ideals play crucial roles in modern algebra and number theory, with modules generalizing vector spaces over rings and ideals serving as special subsets that capture divisibility properties in rings. Applications of ideals include characterizing ring homomorphisms, constructing quotient rings, and formulating prime and maximal ideals critical in algebraic geometry and number theory. Modules facilitate representation theory, homological algebra, and the study of linear algebraic structures over rings, enabling classification of solutions to linear systems and extension of vector space theory.
Relationship between Submodules and Ideals
In ring theory, submodules generalize the concept of ideals within module theory, establishing a foundational relationship where every ideal in a ring can be viewed as a submodule of the ring considered as a module over itself. Submodules maintain the structure of scalar multiplication and additive closure, which parallels the absorption property of ideals under ring multiplication. This connection enables the transfer of concepts like quotient structures and homomorphisms from ideal theory to the broader framework of modules and submodules.
Module Homomorphisms vs Ideal Mappings
Module homomorphisms are structure-preserving maps between modules over a ring, respecting both addition and scalar multiplication, which correspond to linear transformations in vector spaces. Ideal mappings, in contrast, specifically involve ideals as submodules of rings, characterized by being closed under ring multiplication and addition. While every ideal can be viewed as a module, module homomorphisms generalize ideal mappings by allowing a broader class of transformations that preserve module structure without necessarily being tied to ring multiplication properties.
Importance of Modules and Ideals in Modern Algebra
Modules generalize vector spaces by allowing scalars from rings instead of fields, making them crucial for studying linear algebra in broader algebraic structures. Ideals serve as fundamental building blocks in ring theory, enabling the construction of quotient rings and facilitating the analysis of ring homomorphisms. Together, modules and ideals underpin key concepts in modern algebra, such as module homomorphisms, exact sequences, and factorization properties in commutative algebra.
Module Infographic
 libterm.com
libterm.com