Central projection is a geometric transformation that maps points from a three-dimensional object onto a two-dimensional plane through a fixed point called the center of projection. This technique is fundamental in perspective drawing and computer graphics, enabling realistic representations of 3D scenes on flat surfaces. Explore the article to understand how central projection enhances visual accuracy and depth perception.
Table of Comparison
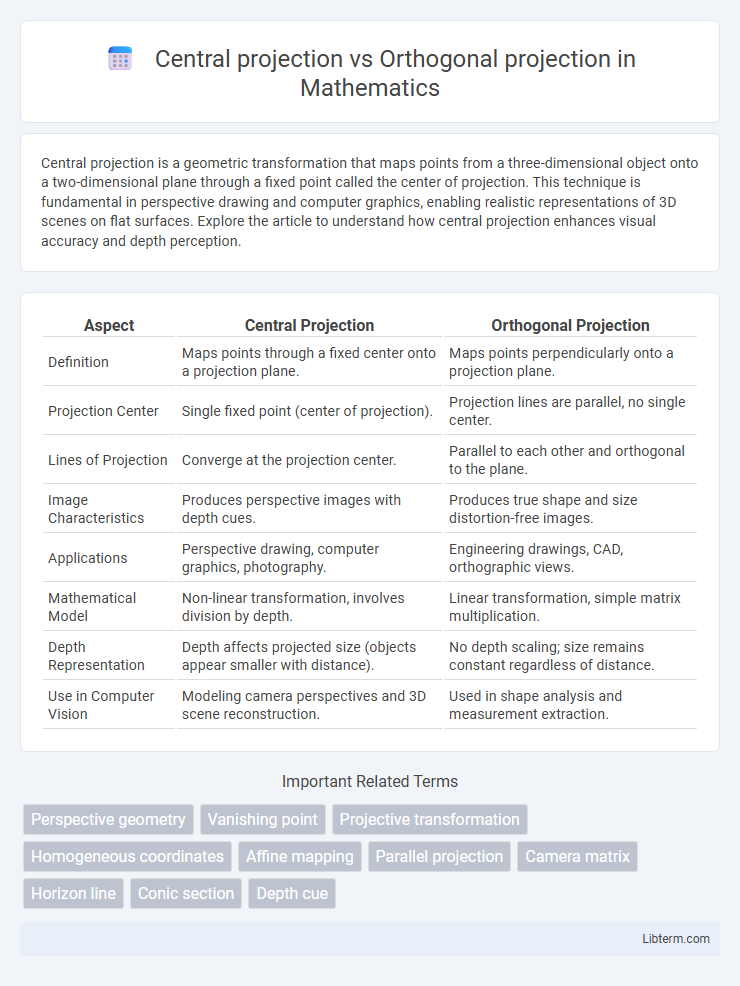
| Aspect | Central Projection | Orthogonal Projection |
|---|---|---|
| Definition | Maps points through a fixed center onto a projection plane. | Maps points perpendicularly onto a projection plane. |
| Projection Center | Single fixed point (center of projection). | Projection lines are parallel, no single center. |
| Lines of Projection | Converge at the projection center. | Parallel to each other and orthogonal to the plane. |
| Image Characteristics | Produces perspective images with depth cues. | Produces true shape and size distortion-free images. |
| Applications | Perspective drawing, computer graphics, photography. | Engineering drawings, CAD, orthographic views. |
| Mathematical Model | Non-linear transformation, involves division by depth. | Linear transformation, simple matrix multiplication. |
| Depth Representation | Depth affects projected size (objects appear smaller with distance). | No depth scaling; size remains constant regardless of distance. |
| Use in Computer Vision | Modeling camera perspectives and 3D scene reconstruction. | Used in shape analysis and measurement extraction. |
Introduction to Central and Orthogonal Projections
Central projection maps three-dimensional objects onto a two-dimensional plane by projecting points along lines converging at a single viewpoint, simulating human eye perspective and preserving depth cues. Orthogonal projection, also known as parallel projection, projects points perpendicular to the projection plane, maintaining true dimensions and shapes without perspective distortion. These projection methods are fundamental in computer graphics, engineering drawings, and architectural visualization for accurately representing spatial relationships.
Definitions: Central Projection Explained
Central projection, also known as perspective projection, involves projecting points from a three-dimensional object onto a projection plane using lines that converge at a single point called the center of projection or the eye point. This technique creates images where objects appear smaller as their distance from the viewer increases, mimicking human visual perception and providing depth cues. In contrast, orthogonal projection uses parallel projection lines perpendicular to the projection plane, preserving true dimensions but lacking perspective effects.
Understanding Orthogonal Projection
Orthogonal projection is a linear transformation where a vector is projected onto a subspace by dropping perpendiculars, preserving angles and distances within the subspace. Unlike central projection, which maps points in three-dimensional space onto a plane through lines converging at a single point (the center), orthogonal projection maintains true scale and shape of objects within the projection plane. This property makes orthogonal projection essential in engineering graphics and computer vision for accurate dimensional representation.
Mathematical Formulation of Central Projection
Central projection is mathematically formulated using homogeneous coordinates, where a 3D point \(P = (X, Y, Z, 1)\) is projected onto a 2D image plane via a projection matrix \(P = K [R | t]\), combining intrinsic parameters \(K\) and extrinsic parameters \([R | t]\). The projection maps point \(P\) to an image point \(p = (x, y, 1)\) through \(p \sim KP\), involving a perspective division by the depth component to account for the camera's viewpoint, resulting in nonlinear transformation with depth-dependent scaling. In contrast, orthogonal projection uses a simpler linear mapping without perspective division, projecting points directly onto the image plane by dropping the depth dimension, making central projection essential for realistic 3D rendering and camera modeling.
Mathematical Formulation of Orthogonal Projection
Orthogonal projection in linear algebra is defined by the formula \( P = A(A^T A)^{-1} A^T \), where \( A \) is the matrix whose columns form an orthonormal basis of the subspace onto which the vector is projected. This projection minimizes the Euclidean distance between the original vector and its image on the subspace, ensuring the residual vector is orthogonal to the subspace. In contrast, central projection involves projecting points onto a plane from a fixed center, resulting in a nonlinear transformation without the orthogonality constraint inherent in the mathematical formulation of orthogonal projection.
Key Differences Between Central and Orthogonal Projections
Central projection maps 3D points onto a 2D plane through a single viewpoint, resulting in perspective distortion where objects farther away appear smaller. Orthogonal projection projects points perpendicularly onto the projection plane, preserving true dimensions and parallelism without perspective effects. The key difference lies in perspective representation, with central projection simulating human vision and orthogonal projection maintaining accurate measurement and scale.
Applications of Central Projection in Real Life
Central projection, commonly known as perspective projection, is widely applied in fields like computer graphics, architectural visualization, and virtual reality to generate realistic images by mimicking how the human eye perceives depth and spatial relationships. It is crucial in photography and cinematography to create immersive visual experiences by projecting three-dimensional scenes onto a two-dimensional plane with vanishing points, enhancing the sense of realism. Central projection also plays a pivotal role in technical drawing and navigation systems, aiding in accurate spatial representation and analysis from a specific viewpoint, unlike orthogonal projection which maintains scale without perspective distortion.
Practical Uses of Orthogonal Projection
Orthogonal projection is widely used in engineering and computer graphics for creating accurate, scalable technical drawings and CAD models, ensuring dimensions remain true to scale without perspective distortion. It simplifies the visualization of complex structures by projecting views onto perpendicular planes, helpful for architectural blueprints and mechanical part designs. Unlike central projection, orthogonal projection facilitates precise measurements and manufacturing processes due to its uniform representation of object dimensions.
Advantages and Limitations of Each Projection Method
Central projection offers a realistic depiction of three-dimensional objects by mimicking the perspective of the human eye, making it ideal for visualizations and simulations, but it can introduce distortion and depth ambiguities. Orthogonal projection preserves true dimensions and parallelism, facilitating accurate measurements and engineering drawings, yet it lacks depth cues and can result in less intuitive spatial representations. Each method balances visual realism and dimensional accuracy, making their selection context-dependent based on visualization or precision needs.
Conclusion: Choosing the Right Projection Technique
Central projection offers realistic depth and perspective, ideal for applications requiring visual depth such as 3D graphics and simulations. Orthogonal projection maintains accurate scale and shape, making it suitable for technical drawings and CAD designs where precise measurements are critical. Selecting the right projection depends on whether visual realism or dimensional accuracy is the primary goal.
Central projection Infographic
 libterm.com
libterm.com