The cup product is a fundamental operation in algebraic topology that combines cohomology classes to form new ones, enhancing the structure of cohomology rings. It enables calculations of intersections and provides insights into the topology of spaces by encoding how different cohomology classes interact. Explore the rest of the article to understand how the cup product enriches your study of topological spaces and their properties.
Table of Comparison
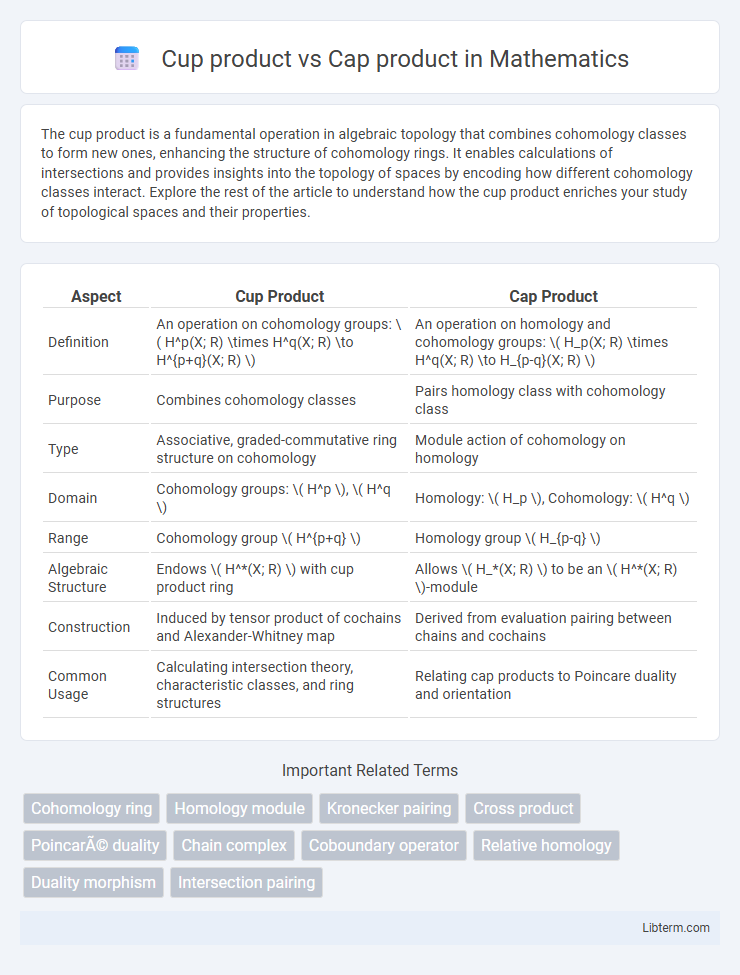
| Aspect | Cup Product | Cap Product |
|---|---|---|
| Definition | An operation on cohomology groups: \( H^p(X; R) \times H^q(X; R) \to H^{p+q}(X; R) \) | An operation on homology and cohomology groups: \( H_p(X; R) \times H^q(X; R) \to H_{p-q}(X; R) \) |
| Purpose | Combines cohomology classes | Pairs homology class with cohomology class |
| Type | Associative, graded-commutative ring structure on cohomology | Module action of cohomology on homology |
| Domain | Cohomology groups: \( H^p \), \( H^q \) | Homology: \( H_p \), Cohomology: \( H^q \) |
| Range | Cohomology group \( H^{p+q} \) | Homology group \( H_{p-q} \) |
| Algebraic Structure | Endows \( H^*(X; R) \) with cup product ring | Allows \( H_*(X; R) \) to be an \( H^*(X; R) \)-module |
| Construction | Induced by tensor product of cochains and Alexander-Whitney map | Derived from evaluation pairing between chains and cochains |
| Common Usage | Calculating intersection theory, characteristic classes, and ring structures | Relating cap products to Poincare duality and orientation |
Introduction to Cup Product and Cap Product
The cup product is a bilinear operation in cohomology that combines two cohomology classes to produce a new class in a higher degree, integral to the algebraic structure of cohomology rings. The cap product, on the other hand, pairs a cohomology class with a homology class, producing a homology class of lower degree and facilitating the interaction between homology and cohomology theories. Both operations are central in algebraic topology, enabling calculations involving the intersection and duality of topological spaces.
Historical Development and Mathematical Context
The Cup product, introduced by Eduard Cech in the 1930s, serves as a fundamental operation in cohomology rings, enabling the combination of cohomology classes to form graded ring structures. The Cap product, developed later within the framework of homology and cohomology interaction, provides a dual operation that pairs cohomology classes with homology chains, reflecting geometric intersection properties. Both products play crucial roles in algebraic topology by establishing algebraic structures that encapsulate topological invariants, with the Cup product emphasizing the cohomological algebra and the Cap product integrating homological intersection theory.
Definitions: Cup Product in Cohomology
The cup product in cohomology is a bilinear operation that combines two cohomology classes to produce a new cohomology class in the combined degree, specifically defined as \( \smile: H^p(X; R) \times H^q(X; R) \to H^{p+q}(X; R) \) for a topological space \(X\) and coefficient ring \(R\). It encodes intersection properties in cohomological terms, representing how cochains multiply and interact within the cochain complex. Unlike the cap product, which pairs homology and cohomology classes to yield homology classes, the cup product uniquely operates within cohomology, enhancing algebraic structures such as the graded ring formed by \( H^*(X; R) \).
Definitions: Cap Product in Homology
The cap product is a bilinear operation between a cohomology class \( \alpha \in H^k(X; R) \) and a homology class \( c \in H_n(X; R) \), producing a homology class \( \alpha \frown c \in H_{n-k}(X; R) \). It acts as a pairing that lowers the dimension of homology by the degree of the cohomology class, reflecting the intersection of cycles with cocycles. This contrasts with the cup product, which combines two cohomology classes \( H^p(X; R) \times H^q(X; R) \to H^{p+q}(X; R) \) to yield a higher-degree cohomology class, emphasizing the dual nature of cap and cup products in algebraic topology.
Algebraic Properties: Graded Structures
The cup product in cohomology endows the cohomology groups with a graded-commutative ring structure, allowing multiplication of classes in differing degrees to produce a class in the sum of those degrees. The cap product defines a graded module action of cohomology on homology, enabling the interaction between cohomology classes and homology classes with a grading that respects the degree shift. Both products preserve graded structures, with the cup product acting internally on cohomology rings and the cap product bridging cohomology and homology via a compatible graded module operation.
Geometric Interpretation
The Cup product in cohomology represents an algebraic operation combining two cohomology classes to form a higher-degree class, often visualized as overlapping dual cells or intersecting subspaces in a space. The Cap product pairs a cohomology class with a homology class, producing a lower-dimensional homology class that can be interpreted geometrically as restricting a cycle to a subspace defined by the cochain. Geometrically, the Cup product corresponds to the intersection of supports of cochains, while the Cap product reflects the action of a cochain "capping" or cutting down a homology cycle.
Computational Techniques and Examples
Cup products are commonly computed using cochain complexes in algebraic topology, where representatives of cohomology classes are combined via cup pairing to produce new cohomology classes. Cap products involve pairing cohomology and homology classes, often calculated by evaluating cochains against chains, enabling intersection number computations or evaluation of homology elements in dual cohomology dimensions. Computational examples include calculating cup products in simplicial cohomology for topological spaces like spheres or tori, and cap products used in intersection homology to analyze geometric structures and manifolds.
Applications in Topology and Geometry
Cup products in cohomology provide an algebraic structure that enables the computation of intersection numbers and characteristic classes in topology, crucial for classifying fiber bundles and manifolds. Cap products link cohomology with homology, facilitating the evaluation of cycles on cohomology classes, which is vital for Poincare duality and the study of manifolds' orientability. Both products are fundamental tools in algebraic topology and differential geometry, enabling deeper insights into manifold invariants and topological quantum field theories.
Key Differences Between Cup and Cap Products
Cup product in algebraic topology combines cohomology classes to produce a new class, operating on cochains and yielding a bilinear graded-commutative ring structure on cohomology. In contrast, the cap product pairs a cohomology class with a homology class to generate a new homology class, providing a module structure of homology over cohomology. The fundamental difference lies in the cup product's role in cohomology ring formation, while the cap product acts as an interaction between homology and cohomology groups.
Conclusion: Significance in Algebraic Topology
The cup product and cap product serve complementary roles in algebraic topology, with the cup product enabling the construction of cohomology ring structures that capture intersection properties of spaces, while the cap product provides a powerful tool to relate homology and cohomology, facilitating Poincare duality. Their interplay is fundamental in analyzing the topological invariants of manifolds, where the cup product defines algebraic operations on cochains and the cap product translates cohomological information into homological contexts. Understanding both products enriches the study of topological spaces by enabling the transition between homology and cohomology theories, essential for classifying and distinguishing manifold structures.
Cup product Infographic
 libterm.com
libterm.com