Lebesgue measure is a fundamental concept in real analysis that provides a way to assign a consistent size or volume to subsets of n-dimensional space, extending the intuitive idea of length, area, and volume. It plays a crucial role in integration theory, allowing more functions to be integrated compared to traditional Riemann integration. Explore the rest of the article to deepen your understanding of Lebesgue measure and its applications.
Table of Comparison
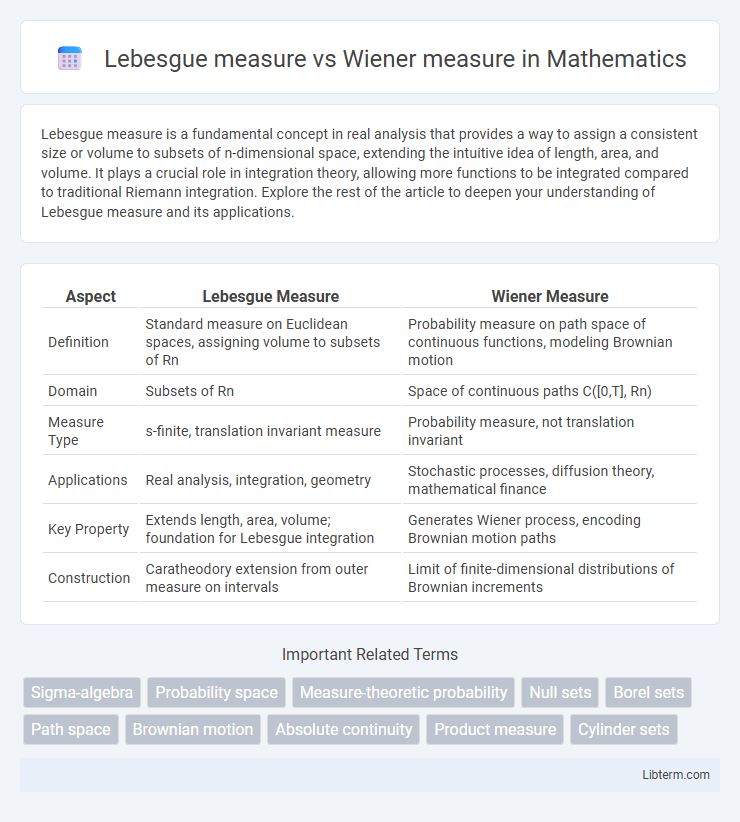
| Aspect | Lebesgue Measure | Wiener Measure |
|---|---|---|
| Definition | Standard measure on Euclidean spaces, assigning volume to subsets of Rn | Probability measure on path space of continuous functions, modeling Brownian motion |
| Domain | Subsets of Rn | Space of continuous paths C([0,T], Rn) |
| Measure Type | s-finite, translation invariant measure | Probability measure, not translation invariant |
| Applications | Real analysis, integration, geometry | Stochastic processes, diffusion theory, mathematical finance |
| Key Property | Extends length, area, volume; foundation for Lebesgue integration | Generates Wiener process, encoding Brownian motion paths |
| Construction | Caratheodory extension from outer measure on intervals | Limit of finite-dimensional distributions of Brownian increments |
Introduction to Measure Theory
Lebesgue measure is a fundamental concept in measure theory, assigning a consistent notion of length, area, or volume to subsets of Euclidean space, which provides the basis for integrating functions in real analysis. Wiener measure, on the other hand, is a probability measure on the space of continuous functions, specifically modeling Brownian motion paths and serving as a cornerstone in stochastic processes and functional integration. Understanding the differences between Lebesgue and Wiener measures illuminates the bridge between classical measure theory and probability theory applied to infinite-dimensional function spaces.
Understanding Lebesgue Measure
Lebesgue measure is a foundational concept in measure theory that assigns a consistent size to subsets of Euclidean space, enabling integration and probability calculations for a wide class of sets. It extends the intuitive notion of length, area, and volume to more complex and potentially irregular sets, facilitating rigorous analysis in real analysis and probability theory. Understanding Lebesgue measure involves grasping concepts like sigma-algebras, measurable sets, and countable additivity, which contrast with the path-dependent structure of Wiener measure in stochastic processes.
Overview of Wiener Measure
Wiener measure is a probability measure on the space of continuous functions, specifically modeling the distribution of Brownian motion paths over a fixed time interval. Unlike Lebesgue measure, which is defined on Euclidean spaces and assigns volume to subsets, Wiener measure captures the stochastic behavior of paths in infinite-dimensional function spaces. This measure plays a crucial role in stochastic analysis, providing the mathematical foundation for studying random processes and diffusion phenomena.
Key Differences: Lebesgue vs Wiener Measures
Lebesgue measure is a fundamental concept in real analysis that assigns a consistent, translation-invariant "size" to subsets of Euclidean space, primarily used for measuring intervals, volumes, and general measurable sets. In contrast, Wiener measure is a probability measure on the space of continuous functions, specifically designed to model Brownian motion paths and capture the stochastic behavior of random processes. Key differences include Lebesgue measure's use in deterministic geometric contexts versus Wiener measure's role in probabilistic and functional analysis contexts, with the latter integrating over infinite-dimensional path spaces rather than finite-dimensional Euclidean space.
Mathematical Formulation of Both Measures
The Lebesgue measure is defined on the sigma-algebra of Lebesgue measurable subsets of Euclidean space, assigning to each set its "volume" via the completion of the standard length or volume measure, often constructed through outer measure and Caratheodory's criterion. In contrast, the Wiener measure is a probability measure on the space of continuous functions starting at zero, formalizing Brownian motion paths, defined through the projective limit of finite-dimensional Gaussian distributions with covariance given by the minimum function. The Wiener measure's mathematical formulation uses the canonical process and reproduces the distribution of standard Brownian motion, while the Lebesgue measure underpins classical integration theory in real analysis.
Applications of Lebesgue Measure
Lebesgue measure plays a fundamental role in real analysis and probability theory by providing a rigorous framework for measuring the size of subsets in Euclidean space, crucial for defining integrals of measurable functions through the Lebesgue integral. Its applications extend to Fourier analysis, where it facilitates the study of function spaces and convergence properties, and to probability theory, underpinning the formulation of continuous probability distributions. In contrast, Wiener measure is essential in stochastic processes, specifically modeling Brownian motion, highlighting the distinct uses of these measures in mathematical analysis and probabilistic modeling.
Applications of Wiener Measure
Wiener measure is a fundamental tool in stochastic analysis, primarily applied in modeling Brownian motion and diffusion processes in fields such as physics, finance, and engineering. Unlike Lebesgue measure, which measures volume in Euclidean spaces, Wiener measure assigns probabilities to paths in infinite-dimensional function spaces, enabling the rigorous treatment of random continuous trajectories. Its applications include the pricing of financial derivatives in the Black-Scholes model, solving stochastic differential equations, and analyzing heat equations via probabilistic methods.
Connections to Probability Theory
Lebesgue measure provides the foundational framework for defining integration and volume in Euclidean spaces, crucial for formulating probabilities related to continuous random variables. Wiener measure extends these concepts by assigning probabilities to paths of Brownian motion, enabling rigorous analysis of stochastic processes in functional spaces. Both measures are essential in probability theory, with Lebesgue measure underpinning standard probability distributions and Wiener measure facilitating the study of diffusion and martingale properties.
Common Misconceptions and Challenges
Lebesgue measure, a translation-invariant measure on Euclidean space, is often mistaken as suitable for infinite-dimensional path spaces, where Wiener measure--a probability measure on continuous function space representing Brownian motion--applies instead. A common misconception is treating Wiener measure as absolutely continuous with respect to Lebesgue measure; in reality, Wiener measure is singular and concentrates on fractal-like paths, posing challenges in applying standard measure-theoretic techniques. The infinite-dimensional nature of Wiener measure introduces complexities in integration and differentiation, requiring advanced stochastic calculus tools not needed for classical Lebesgue measure.
Summary and Further Reading
Lebesgue measure provides a foundational framework for measuring subsets of Euclidean space, essential for integration theory and real analysis, while Wiener measure specializes in assigning probabilities to paths in continuous-time stochastic processes, particularly Brownian motion. Both measures play critical roles in their respective areas: Lebesgue measure underpins classical analysis, whereas Wiener measure is central to the mathematical theory of diffusion processes and stochastic calculus. For deeper insights, consult texts like "Real Analysis" by Royden and "Brownian Motion and Stochastic Calculus" by Karatzas and Shreve.
Lebesgue measure Infographic
 libterm.com
libterm.com