The supremum, or least upper bound, of a set is the smallest value that is greater than or equal to every element in that set, playing a crucial role in mathematical analysis and optimization problems. Understanding how to identify and apply supremum concepts can enhance your ability to solve inequalities and analyze functions effectively. Explore the rest of the article to deepen your grasp of supremum and its applications in various mathematical contexts.
Table of Comparison
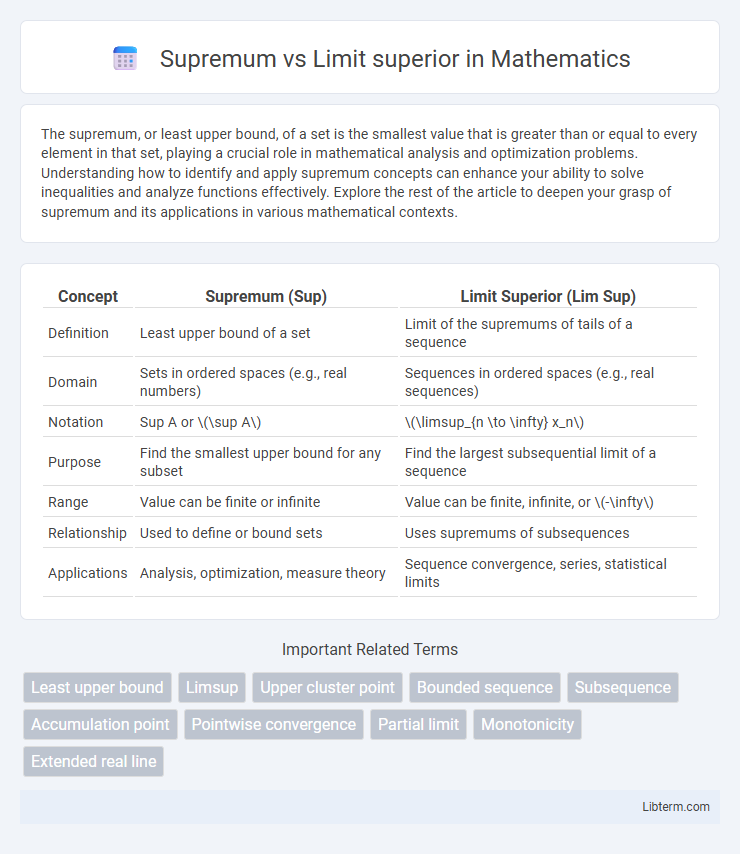
| Concept | Supremum (Sup) | Limit Superior (Lim Sup) |
|---|---|---|
| Definition | Least upper bound of a set | Limit of the supremums of tails of a sequence |
| Domain | Sets in ordered spaces (e.g., real numbers) | Sequences in ordered spaces (e.g., real sequences) |
| Notation | Sup A or \(\sup A\) | \(\limsup_{n \to \infty} x_n\) |
| Purpose | Find the smallest upper bound for any subset | Find the largest subsequential limit of a sequence |
| Range | Value can be finite or infinite | Value can be finite, infinite, or \(-\infty\) |
| Relationship | Used to define or bound sets | Uses supremums of subsequences |
| Applications | Analysis, optimization, measure theory | Sequence convergence, series, statistical limits |
Introduction to Supremum and Limit Superior
Supremum, or least upper bound, of a set is the smallest value that is greater than or equal to every element in the set, providing a crucial measure in real analysis and optimization problems. Limit superior, often denoted as lim sup, extends this concept to sequences by identifying the supremum of the set of subsequential limits, capturing the long-term upper behavior of the sequence elements. Both supremum and limit superior serve as fundamental tools in understanding boundedness and convergence properties in mathematical analysis.
Definitions: Supremum Explained
The supremum, or least upper bound, of a set is the smallest value that is greater than or equal to every element in that set, whether or not it belongs to the set itself. In contrast, the limit superior (lim sup) is a concept from sequence analysis representing the supremum of the set of subsequential limits, capturing the long-term upper behavior of a sequence. Understanding the supremum helps clarify the limit superior as it extends the idea of a maximum to infinite sequences and their eventual upper bounds.
Understanding Limit Superior (lim sup)
Limit superior (lim sup) of a sequence represents the greatest accumulation point or the supremum of its tail subsequences, capturing the largest value that the terms approach infinitely often. It differs from the standard supremum, which is the least upper bound of the entire sequence regardless of tail behavior. Understanding lim sup is essential for analyzing convergence in sequences with oscillations, as it highlights the upper boundary of limit points rather than a fixed maximum.
Key Differences Between Supremum and Limit Superior
The supremum of a set is the least upper bound that may or may not belong to the set, providing a precise boundary for the values within it, while the limit superior (lim sup) of a sequence is the supremum of its subsequential limits, describing the behavior of the sequence's tail in the limit. Key differences include that the supremum is a static property of a set at a fixed point, whereas the limit superior is a dynamic property capturing the asymptotic upper bounds of a sequence. Supremum applies to sets in general, whereas limit superior specifically applies to sequences and conveys information about their convergence patterns over infinity.
Mathematical Notation and Representation
The supremum of a set \( A \), denoted \(\sup A\), is the smallest upper bound of \( A \) within a given ordered set, whereas the limit superior of a sequence \(\{a_n\}\), written as \(\limsup_{n \to \infty} a_n\), represents the limit of the supremums of the sequence's tails: \(\lim_{n \to \infty} \sup_{k \geq n} a_k\). Mathematically, \(\sup A = \inf \{x \in \mathbb{R} : a \leq x \text{ for all } a \in A\}\), and \(\limsup_{n \to \infty} a_n = \inf_{n} \sup_{k \geq n} a_k\), illustrating the supremum as a static bound and the limit superior as a dynamic measure converging over infinite subsequences.
Properties of Supremum
The supremum of a set is the least upper bound, ensuring no element exceeds it while being minimal among all such bounds. It is always greater than or equal to every element in the set and, if the supremum is an element of the set, it corresponds to the maximum. Unlike the limit superior, which applies to sequences and their subsequential limits, the supremum strictly pertains to the ordering in the set and provides foundational bounds used in defining limit superior.
Properties of Limit Superior
The limit superior of a sequence is defined as the supremum of the set of its subsequential limits, capturing the largest cluster point. It is always greater than or equal to the supremum of the tail sequence from any index onward, ensuring non-increasing behavior as the index grows. This property guarantees that the limit superior provides the least upper bound on the tail behavior of the sequence, reflecting its eventual upper bound behavior.
Examples Illustrating Supremum and Limit Superior
Consider the sequence \(a_n = (-1)^n \left(1 - \frac{1}{n}\right)\), where the supremum is 1 as values approach 1 from below and above for even terms. The limit superior of this sequence is also 1, capturing the eventual upper bound of the subsequence formed by the even-indexed terms. In contrast, for the sequence \(b_n = \frac{(-1)^n}{n}\), the supremum is 1 while the limit superior is 0, reflecting how the values diminish over time despite the initial maximum.
Applications in Real Analysis and Sequences
The supremum of a sequence represents the least upper bound of its range, offering a precise bound for function values or sequence elements crucial in optimization problems and convergence analysis. Limit superior, or lim sup, generalizes this concept by capturing the eventual superior behavior of the sequence, identifying the largest accumulation point and providing insight into the subsequential limits. These tools are fundamental in real analysis for studying the convergence properties of sequences, bounding function values, and analyzing oscillatory or non-convergent behaviors in sequences.
Common Mistakes and How to Avoid Them
Confusing the supremum with the limit superior often leads to errors in sequence analysis, as the supremum represents the least upper bound of a set, while the limit superior captures the eventual upper limit of a sequence's subsequential limits. A common mistake is assuming the limit superior equals the supremum of the entire sequence, which disregards fluctuations and tail behavior in infinite sequences. Avoid this by carefully differentiating between set bounds and limit concepts, verifying whether the sequence's behavior at infinity aligns with supremum definitions or the more nuanced limit superior criteria.
Supremum Infographic
 libterm.com
libterm.com