Jacobi polynomials play a crucial role in approximation theory and numerical analysis due to their orthogonality properties on the interval [-1, 1] with respect to the weight function (1-x)^a (1+x)^b. These polynomials generalize several classical orthogonal polynomials, making them essential in solving differential equations and expanding functions in series. Explore the rest of the article to understand how Jacobi polynomials can enhance your mathematical toolkit.
Table of Comparison
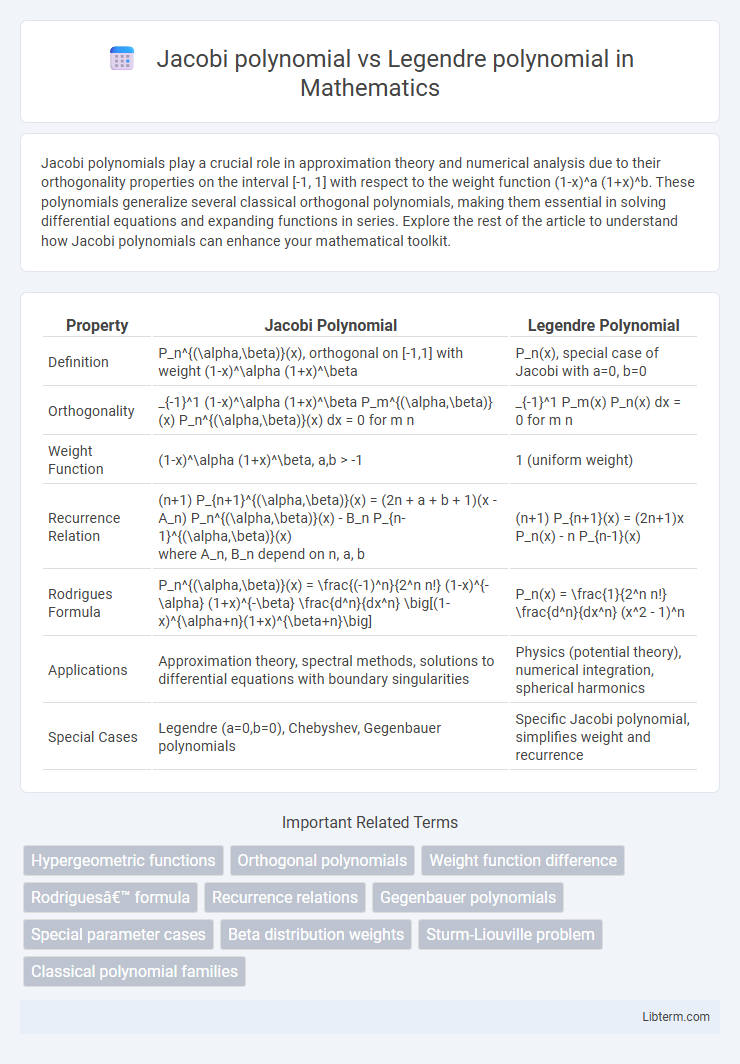
| Property | Jacobi Polynomial | Legendre Polynomial |
|---|---|---|
| Definition | P_n^{(\alpha,\beta)}(x), orthogonal on [-1,1] with weight (1-x)^\alpha (1+x)^\beta | P_n(x), special case of Jacobi with a=0, b=0 |
| Orthogonality | _{-1}^1 (1-x)^\alpha (1+x)^\beta P_m^{(\alpha,\beta)}(x) P_n^{(\alpha,\beta)}(x) dx = 0 for m n | _{-1}^1 P_m(x) P_n(x) dx = 0 for m n |
| Weight Function | (1-x)^\alpha (1+x)^\beta, a,b > -1 | 1 (uniform weight) |
| Recurrence Relation |
(n+1) P_{n+1}^{(\alpha,\beta)}(x) = (2n + a + b + 1)(x - A_n) P_n^{(\alpha,\beta)}(x) - B_n P_{n-1}^{(\alpha,\beta)}(x)
where A_n, B_n depend on n, a, b |
(n+1) P_{n+1}(x) = (2n+1)x P_n(x) - n P_{n-1}(x) |
| Rodrigues Formula | P_n^{(\alpha,\beta)}(x) = \frac{(-1)^n}{2^n n!} (1-x)^{-\alpha} (1+x)^{-\beta} \frac{d^n}{dx^n} \big[(1-x)^{\alpha+n}(1+x)^{\beta+n}\big] | P_n(x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} (x^2 - 1)^n |
| Applications | Approximation theory, spectral methods, solutions to differential equations with boundary singularities | Physics (potential theory), numerical integration, spherical harmonics |
| Special Cases | Legendre (a=0,b=0), Chebyshev, Gegenbauer polynomials | Specific Jacobi polynomial, simplifies weight and recurrence |
Introduction to Orthogonal Polynomials
Jacobi polynomials generalize Legendre polynomials by introducing two parameters \(\alpha\) and \(\beta\), allowing them to form a family of orthogonal polynomials on the interval \([-1, 1]\) with weight function \((1-x)^\alpha (1+x)^\beta\). Legendre polynomials are a special case of Jacobi polynomials with \(\alpha = \beta = 0\), orthogonal with respect to the constant weight function 1 on \([-1, 1]\). Both polynomial families play crucial roles in solving differential equations, numerical integration, and spectral methods by providing bases of orthogonal functions in various weighted Hilbert spaces.
Overview of Jacobi Polynomials
Jacobi polynomials are a class of classical orthogonal polynomials defined on the interval [-1, 1] with weight function \((1 - x)^\alpha (1 + x)^\beta\), where \(\alpha, \beta > -1\). They generalize Legendre polynomials, which correspond to the special case \(\alpha = \beta = 0\), and arise as solutions to the Jacobi differential equation important in spectral methods and approximation theory. Jacobi polynomials possess recurrence relations, Rodrigues' formula, and orthogonality properties essential for expansions in weighted \(L^2\) spaces and applications in numerical analysis and mathematical physics.
Overview of Legendre Polynomials
Legendre polynomials form a sequence of orthogonal polynomials with respect to the weight function 1 on the interval [-1, 1], serving as a special case of Jacobi polynomials where both parameters a and b equal zero. They play a crucial role in solving Legendre's differential equation and appear frequently in problems of physics involving spherical symmetry, such as gravitational and electrostatic potentials. Their orthogonality property and recurrence relations make them fundamental tools in numerical analysis, approximation theory, and spectral methods.
Mathematical Definitions and Properties
Jacobi polynomials \( P_n^{(\alpha,\beta)}(x) \) are a family of orthogonal polynomials defined by the hypergeometric function \({}_2F_1\) with parameters \(\alpha, \beta > -1\), satisfying the differential equation \((1-x^2)y'' + [\beta-\alpha-(\alpha+\beta+2)x]y' + n(n+\alpha+\beta+1)y=0\). Legendre polynomials \( P_n(x) \) are a special case of Jacobi polynomials with \(\alpha = \beta = 0\), simplifying the weight function to 1 and the differential equation to \((1-x^2)y'' - 2xy' + n(n+1)y = 0\). Both sets are orthogonal with respect to their weight functions on the interval \([-1,1]\), with Jacobi polynomials having weight \( (1-x)^\alpha (1+x)^\beta \) and Legendre polynomials exhibiting orthogonality under the uniform weight.
Weight Functions and Orthogonality Conditions
Jacobi polynomials \(P_n^{(\alpha,\beta)}(x)\) are orthogonal with respect to the weight function \((1-x)^\alpha (1+x)^\beta\) on the interval \([-1,1]\), where \(\alpha, \beta > -1\), allowing for flexible tuning of endpoint behavior. Legendre polynomials \(P_n(x)\) are a special case of Jacobi polynomials with \(\alpha = \beta = 0\), exhibiting orthogonality under the uniform weight function \(w(x) = 1\) on \([-1,1]\). Both polynomial families satisfy distinct orthogonality conditions, enabling their widespread application in solving differential equations and numerical integration problems where specific weight functions are critical.
Special Cases: Legendre as a Subset of Jacobi
Legendre polynomials are a special case of Jacobi polynomials when the parameters a and b both equal zero, denoted as P_n^(0,0)(x). This subset relationship highlights that Legendre polynomials inherit orthogonality properties on the interval [-1,1] with weight function w(x) = 1, a special instance of the more general Jacobi weight w(x) = (1-x)^a(1+x)^b. The generality of Jacobi polynomials allows adaptation to boundary behaviors and weighting schemes beyond those covered by Legendre polynomials.
Recurrence Relations and Generating Functions
Jacobi polynomials \(P_n^{(\alpha,\beta)}(x)\) satisfy a three-term recurrence relation involving parameters \(\alpha\) and \(\beta\), expressed as \( a_n P_{n+1}^{(\alpha,\beta)}(x) = (b_n x + c_n) P_n^{(\alpha,\beta)}(x) - d_n P_{n-1}^{(\alpha,\beta)}(x) \), where \(a_n, b_n, c_n, d_n\) depend on \(n, \alpha, \beta\). Legendre polynomials \(P_n(x)\) are a special case of Jacobi polynomials with \(\alpha = \beta = 0\), satisfying the simpler recurrence \( (n+1) P_{n+1}(x) = (2n+1) x P_n(x) - n P_{n-1}(x) \). The generating function for Jacobi polynomials is given by \( G(t,x) = 2^{\alpha+\beta} R (1 - t + R)^{-\alpha} (1 + t + R)^{-\beta} \) with \( R = (1 - 2 t x + t^2)^{1/2} \), while the Legendre polynomial generating function simplifies to \( (1 - 2 x t + t^2)^{-1/2} \).
Applications in Numerical Analysis and Physics
Jacobi polynomials and Legendre polynomials are widely used in numerical analysis for solving differential equations and performing spectral methods, with Jacobi polynomials offering greater flexibility due to their dependence on two parameters, a and b, allowing tailored weight functions for complex boundary conditions. In physics, Legendre polynomials frequently arise in problems involving spherical harmonics and potential theory, particularly in solving Laplace's equation for systems with spherical symmetry, while Jacobi polynomials are employed in quantum mechanics and approximation theory where variable endpoint weights are essential. The orthogonality properties of both polynomial families enable efficient computation of expansions and integrals, making them indispensable tools for high-precision numerical simulations and analytical solutions in scientific research.
Comparative Analysis: Jacobi vs Legendre
Jacobi polynomials, defined by two parameters a and b, generalize Legendre polynomials, which are a special case with a=b=0, providing greater flexibility for weighting functions on the interval [-1,1]. While Legendre polynomials are orthogonal with respect to a uniform weight function, Jacobi polynomials accommodate weighted orthogonality, enabling more tailored solutions in spectral methods and approximation theory. The comparative analysis reveals Jacobi polynomials' superior adaptability in solving differential equations with varying boundary conditions, whereas Legendre polynomials are preferred for problems requiring simplicity and uniform weighting.
Conclusion and Further Reading
Jacobi polynomials generalize Legendre polynomials by introducing two parameters that allow greater flexibility in weight functions, making them useful in more diverse orthogonal polynomial applications. Legendre polynomials are a special case of Jacobi polynomials with both parameters set to zero, commonly applied in solving problems with spherical symmetry in physics and engineering. For further reading, explore "Orthogonal Polynomials" by Gabor Szego and research articles on spectral methods detailing applications in numerical analysis and computational physics.
Jacobi polynomial Infographic
 libterm.com
libterm.com