Inaccessible cardinals are large cardinal numbers in set theory that cannot be reached by standard set-theoretic operations such as power sets and unions, marking them as pivotal in understanding the hierarchy of infinite sizes. These cardinals are fundamental in exploring advanced mathematical concepts related to consistency strength and the foundations of mathematics. Discover how inaccessible cardinals shape modern set theory and why they matter for your grasp of mathematical infinity by reading further.
Table of Comparison
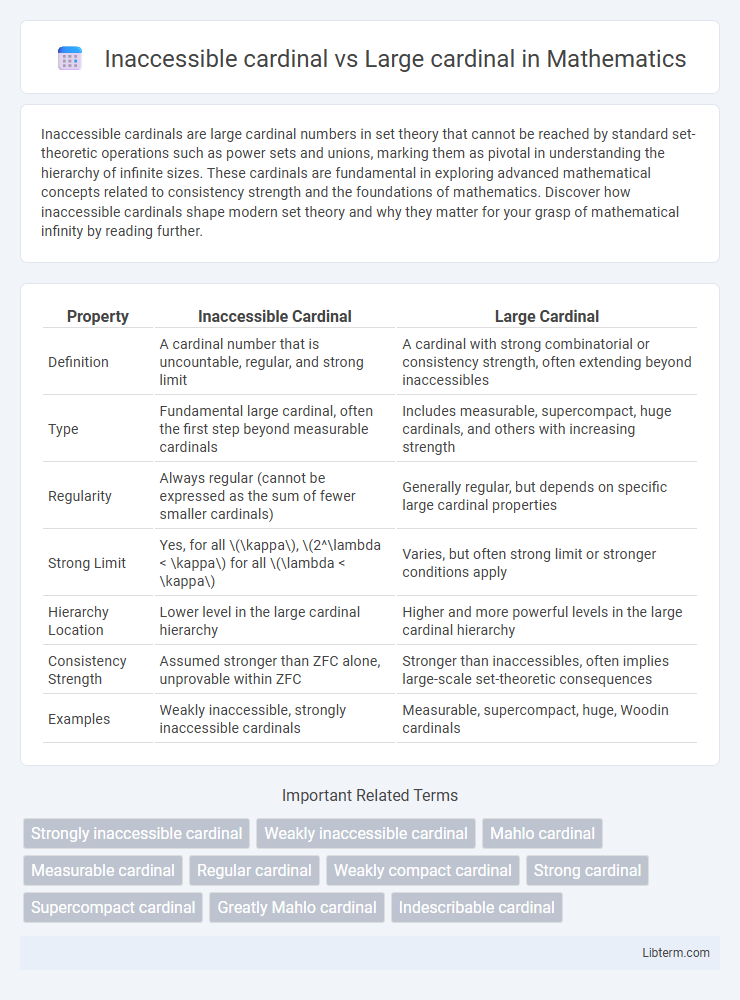
| Property | Inaccessible Cardinal | Large Cardinal |
|---|---|---|
| Definition | A cardinal number that is uncountable, regular, and strong limit | A cardinal with strong combinatorial or consistency strength, often extending beyond inaccessibles |
| Type | Fundamental large cardinal, often the first step beyond measurable cardinals | Includes measurable, supercompact, huge cardinals, and others with increasing strength |
| Regularity | Always regular (cannot be expressed as the sum of fewer smaller cardinals) | Generally regular, but depends on specific large cardinal properties |
| Strong Limit | Yes, for all \(\kappa\), \(2^\lambda < \kappa\) for all \(\lambda < \kappa\) | Varies, but often strong limit or stronger conditions apply |
| Hierarchy Location | Lower level in the large cardinal hierarchy | Higher and more powerful levels in the large cardinal hierarchy |
| Consistency Strength | Assumed stronger than ZFC alone, unprovable within ZFC | Stronger than inaccessibles, often implies large-scale set-theoretic consequences |
| Examples | Weakly inaccessible, strongly inaccessible cardinals | Measurable, supercompact, huge, Woodin cardinals |
Introduction to Cardinal Numbers
Inaccessible cardinals represent a special class of large cardinals characterized by strong combinatorial and structural properties that surpass the limits of smaller infinite cardinalities. Cardinal numbers measure the size of sets, with large cardinals like inaccessible cardinals indicating immense infinite sizes not reachable through standard set-theoretic operations. These cardinals play a foundational role in set theory, often serving as benchmarks for the hierarchy of infinite sizes and consistency strength in mathematical logic.
Overview of Large Cardinals
Large cardinals represent a hierarchy of infinite cardinal numbers with strong combinatorial properties extending beyond standard set theory axioms. Inaccessible cardinals form a fundamental subclass of large cardinals characterized by regularity and strong limit properties, serving as critical benchmarks in the study of set-theoretic universes. These cardinals demonstrate increasing levels of consistency strength, supporting deep results in model theory and the foundations of mathematics.
Defining Inaccessible Cardinals
Inaccessible cardinals are a foundational concept in set theory, defined as uncountable regular strong limit cardinals that cannot be reached by standard set-theoretic operations like power set or union from smaller cardinals. These cardinals serve as critical benchmarks for the existence of large cardinals, which extend beyond them with properties such as measurability or supercompactness. Understanding inaccessible cardinals is essential for exploring hierarchies of large cardinals and their implications in higher-order infinity and consistency strength.
Properties of Inaccessible Cardinals
Inaccessible cardinals are a specific type of large cardinal characterized by strong closure properties and uncountability, making them limit cardinals that cannot be reached by standard set-theoretic operations such as powersets or unions of smaller cardinals. They are regular cardinals, meaning their cofinality equals the cardinal itself, and are strong limit cardinals because for any smaller cardinal \(\kappa < \lambda\), \(2^\kappa < \lambda\) holds. This combination of regularity and the strong limit property defines the foundational strength of inaccessible cardinals within the hierarchy of large cardinals, distinguishing them from other large cardinal notions.
Hierarchy within Large Cardinals
Inaccessible cardinals represent an early level in the hierarchy of large cardinals, characterized by their uncountability, strong limit properties, and regularity. Large cardinals extend beyond inaccessibles, encompassing stronger axioms such as Mahlo, measurable, and supercompact cardinals, each with increasing consistency strength and structural complexity. This hierarchy organizes large cardinal concepts by ascending consistency strength, reflecting deeper foundational properties in set theory.
Inaccessible Cardinals vs Other Large Cardinals
Inaccessible cardinals are a fundamental class of large cardinals defined by their uncountability, regularity, and strong limit properties, distinguishing them from other large cardinals by their role as minimal large cardinal notions. Unlike measurable or supercompact cardinals, which possess stronger embedding properties and higher consistency strength, inaccessible cardinals serve as critical benchmarks in the hierarchy of large cardinals. Their significance lies in providing a foundation for constructing and comparing various large cardinal axioms within set theory.
Set-Theoretic Significance
Inaccessible cardinals serve as a foundational benchmark in set theory, representing a minimal form of large cardinal that cannot be reached by standard set operations from smaller cardinals, thereby ensuring the existence of rich, well-structured universes. Large cardinals encompass a hierarchy including inaccessible, measurable, and supercompact cardinals, each introducing stronger consistency assumptions and deeper combinatorial properties that extend the expressive power of set theory. Their set-theoretic significance lies in providing consistency strength calibrations for various hypotheses and enabling the exploration of models that reveal fundamental aspects of the infinite.
Consistency and Independence Results
Inaccessible cardinals are a fundamental class of large cardinals characterized by strong closure properties and are often used to establish the consistency strength of various set-theoretic axioms. Large cardinals extend beyond inaccessibles, such as measurable and Woodin cardinals, providing a hierarchy that measures increasingly stronger forms of infinity and their implications for consistency. Independence results in set theory often rely on large cardinal assumptions, demonstrating that certain propositions cannot be proved or disproved within standard ZFC axioms, with inaccessible cardinals marking the lower bounds of these consistency strengths.
Applications in Mathematical Logic
Inaccessible cardinals serve as fundamental building blocks in set theory, providing essential frameworks for constructing models that exhibit strong closure properties and enabling consistency proofs within higher-order logics. Large cardinals, broadly encompassing inaccessible cardinals, extend these capabilities by introducing stronger hypotheses that yield profound insights into the structure of the set-theoretic universe and facilitate advanced results in determinacy and inner model theory. Applications in mathematical logic leverage inaccessible and larger cardinals to analyze the hierarchies of definability, prove independence results, and explore the boundaries of provability in formal systems.
Conclusion: Comparing Inaccessible and Large Cardinals
Inaccessible cardinals serve as foundational examples of large cardinals, characterized by strong regularity and limit properties, whereas large cardinals encompass a broader spectrum with increasingly stronger axioms extending beyond inaccessibility. The hierarchy shows inaccessible cardinals as initial milestones, while other large cardinals like measurable or supercompact exhibit greater consistency strength and profound implications for set theory. Comparing these reveals the foundational role of inaccessibles and the progressive strength and complexity captured by larger cardinal notions.
Inaccessible cardinal Infographic
 libterm.com
libterm.com