A ruled surface is generated by moving a straight line along a predetermined path, creating shapes like hyperbolic paraboloids and helicoids that are essential in architecture and engineering. These surfaces are characterized by their unique geometric properties, making them highly useful for structural designs and manufacturing processes. Explore this article to understand how ruled surfaces can transform your design projects with efficiency and elegance.
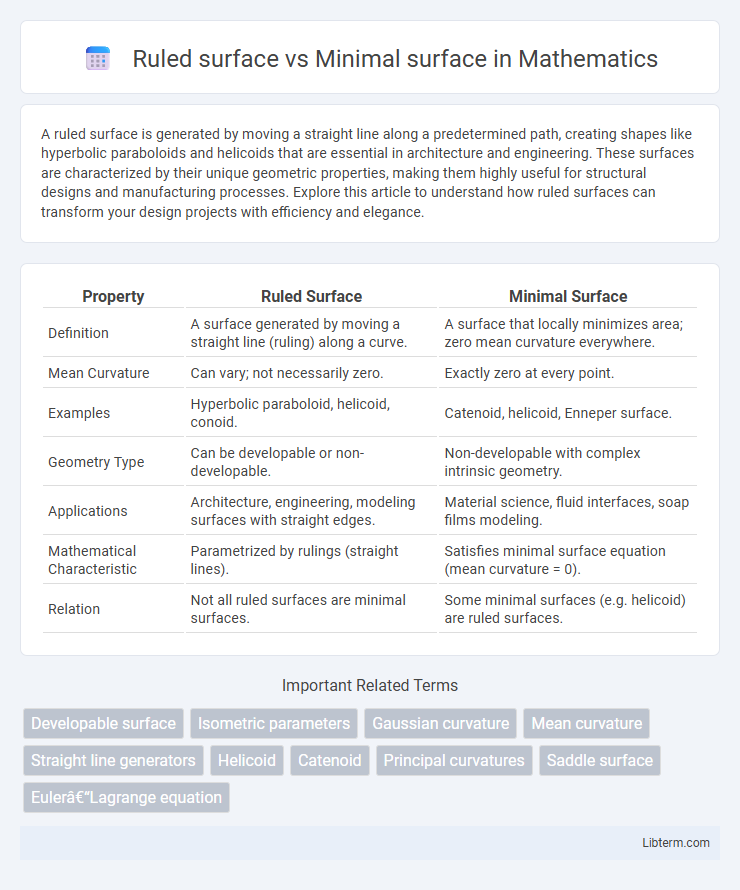
Table of Comparison
| Property | Ruled Surface | Minimal Surface |
|---|---|---|
| Definition | A surface generated by moving a straight line (ruling) along a curve. | A surface that locally minimizes area; zero mean curvature everywhere. |
| Mean Curvature | Can vary; not necessarily zero. | Exactly zero at every point. |
| Examples | Hyperbolic paraboloid, helicoid, conoid. | Catenoid, helicoid, Enneper surface. |
| Geometry Type | Can be developable or non-developable. | Non-developable with complex intrinsic geometry. |
| Applications | Architecture, engineering, modeling surfaces with straight edges. | Material science, fluid interfaces, soap films modeling. |
| Mathematical Characteristic | Parametrized by rulings (straight lines). | Satisfies minimal surface equation (mean curvature = 0). |
| Relation | Not all ruled surfaces are minimal surfaces. | Some minimal surfaces (e.g. helicoid) are ruled surfaces. |
Introduction to Ruled and Minimal Surfaces
Ruled surfaces are generated by moving a straight line along a curve, characterized by their linear generators, making them fundamental in architectural and engineering designs. Minimal surfaces minimize surface area subject to boundary conditions, exhibiting zero mean curvature, which is critical in material science and fluid mechanics. Both surfaces are studied extensively in differential geometry for their unique curvature properties and applications in optimizing structural efficiency.
Defining Ruled Surfaces
Ruled surfaces are defined as surfaces generated by moving a straight line along a curve, with each point on the surface lying on a straight line called a ruling. These surfaces include cylindrical, conical, and hyperbolic paraboloid shapes that exhibit linear elements in their structure. Unlike minimal surfaces that minimize area and often have complex curvature, ruled surfaces are characterized primarily by their linear generatrices.
Defining Minimal Surfaces
Minimal surfaces are defined as surfaces with zero mean curvature at every point, representing critical points for the area functional under variations. Ruled surfaces consist of straight lines, but not all ruled surfaces qualify as minimal since they generally have nonzero mean curvature. Classical examples of minimal surfaces include the catenoid and helicoid, which minimize area locally despite their complex geometry.
Geometric Properties Comparison
Ruled surfaces are characterized by straight lines called rulings that sweep through space, making them inherently developable or allowing simple geometric construction, while minimal surfaces minimize mean curvature and exhibit intricate curvature distributions with zero average curvature at every point. The Gaussian curvature of ruled surfaces varies widely but can be zero if developable, whereas minimal surfaces have negative or zero Gaussian curvature, reflecting their saddle-like or planar geometry. The distinct geometric properties influence their applications: ruled surfaces are prominent in architectural design for their structural simplicity, whereas minimal surfaces optimize material usage and surface area in nature and engineering.
Formation and Construction Methods
Ruled surfaces are generated by moving a straight line along two or more guiding curves, forming a surface composed entirely of straight lines, often constructed through linear interpolation techniques or using parametric equations. Minimal surfaces arise from variational principles minimizing surface area while maintaining boundary conditions, typically constructed via calculus of variations, partial differential equations, or computational methods like finite element analysis. The formation of ruled surfaces emphasizes geometric simplicity and ease of construction, whereas minimal surfaces focus on achieving equilibrium shapes characterized by zero mean curvature.
Mathematical Equations and Parameters
Ruled surfaces are generated by moving a straight line along a curve, mathematically expressed as \( \mathbf{R}(u,v) = \mathbf{c}(u) + v \mathbf{d}(u) \), where \( \mathbf{c}(u) \) is a base curve and \( \mathbf{d}(u) \) is a direction vector. Minimal surfaces satisfy the zero mean curvature condition \( H = 0 \), governed by the nonlinear partial differential equation \( (1 + z_y^2) z_{xx} - 2 z_x z_y z_{xy} + (1 + z_x^2) z_{yy} = 0 \). While ruled surfaces focus on linear parametric forms involving lines, minimal surfaces require solving elliptic PDEs related to surface tension and area minimization under boundary constraints.
Visual Examples and Iconic Structures
Ruled surfaces, characterized by straight lines moving along curves, are visually exemplified by the hyperboloid structures in the cooling towers of power plants and the elegant design of the Eiffel Tower. Minimal surfaces, defined by zero mean curvature and often appearing in soap films, inspire iconic architecture such as the roofs of Munich's Olympic Stadium with their smooth, tension-minimized forms. Comparing these surfaces highlights ruled surfaces' linear geometric patterns versus minimal surfaces' fluid, organic aesthetics in architectural design.
Applications in Architecture and Engineering
Ruled surfaces, characterized by straight lines swept along a curve, are extensively used in architecture and engineering for creating visually striking structures like hyperbolic paraboloids and saddle roofs, offering ease of construction and material efficiency. Minimal surfaces, defined by zero mean curvature and natural tension minimization, inspire efficient designs in lightweight tensile structures, membranes, and shells that optimize load distribution and stability. Both surface types enable innovative, sustainable architectural forms by balancing aesthetic appeal with structural performance in modern engineering projects.
Advantages and Limitations of Each Surface
Ruled surfaces offer simplicity in construction and straightforward geometric representation, making them ideal for architectural structures and engineering applications where linear elements dominate. Minimal surfaces, characterized by their minimal area and mean curvature zero, provide optimal material efficiency and structural stability in designs like soap films and membrane structures. While ruled surfaces may lack optimal stress distribution and have limitations in complex curvature, minimal surfaces can be computationally intensive to model and fabricate due to their complex, nonlinear geometry.
Summary: Key Differences and Use Cases
Ruled surfaces are generated by moving a straight line along a curve, commonly used in architectural designs and manufacturing for their structural simplicity and ease of construction. Minimal surfaces minimize surface area under boundary constraints, making them ideal for applications in material science and biological membranes where efficient energy distribution is critical. The key difference lies in their geometric properties: ruled surfaces emphasize linearity and simplicity, while minimal surfaces focus on curvature optimization and surface tension balance.
Ruled surface Infographic
 libterm.com
libterm.com