A rational base point is a crucial concept in mathematics, particularly in number theory and algebraic geometry, referring to a specific point on an algebraic curve with coordinates in a given rational field. Understanding the properties of rational base points can deepen your insight into the structure and solutions of polynomial equations. Explore the rest of the article to discover how rational base points impact complex mathematical theories and applications.
Table of Comparison
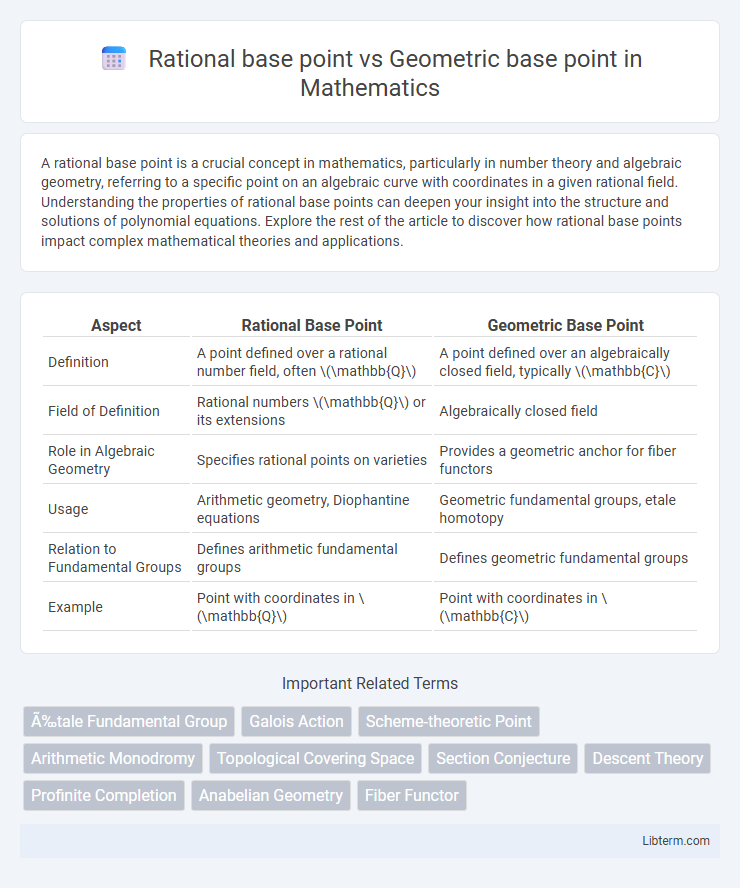
| Aspect | Rational Base Point | Geometric Base Point |
|---|---|---|
| Definition | A point defined over a rational number field, often \(\mathbb{Q}\) | A point defined over an algebraically closed field, typically \(\mathbb{C}\) |
| Field of Definition | Rational numbers \(\mathbb{Q}\) or its extensions | Algebraically closed field |
| Role in Algebraic Geometry | Specifies rational points on varieties | Provides a geometric anchor for fiber functors |
| Usage | Arithmetic geometry, Diophantine equations | Geometric fundamental groups, etale homotopy |
| Relation to Fundamental Groups | Defines arithmetic fundamental groups | Defines geometric fundamental groups |
| Example | Point with coordinates in \(\mathbb{Q}\) | Point with coordinates in \(\mathbb{C}\) |
Introduction to Base Points
Base points serve as fundamental references for defining coordinate systems in mathematics and geometry. Rational base points are defined using rational numbers, facilitating exact calculations and algebraic manipulations in fields like number theory and algebraic geometry. Geometric base points rely on spatial positioning and often use points in Euclidean space, supporting intuitive visualization and geometric constructions.
Defining Rational Base Points
Defining rational base points involves selecting points on algebraic varieties whose coordinates lie within a given number field, typically the rational numbers, enabling arithmetic operations and Diophantine analysis. These points differ from geometric base points, which may exist over algebraic closures or arbitrary field extensions and serve more general geometric or topological purposes. Rational base points play a crucial role in arithmetic geometry, particularly in the study of rational solutions, Galois representations, and arithmetic fundamental groups.
Understanding Geometric Base Points
Geometric base points represent points over algebraic closures, allowing for a more comprehensive view of algebraic varieties beyond rational base points defined strictly over fields of definition. Understanding geometric base points is crucial for studying properties stable under field extensions, such as fundamental groups and coverings in algebraic geometry. This concept provides a framework for analyzing schemes and morphisms in a way that accounts for all algebraic points, enhancing the ability to compare geometric and arithmetic structures.
Key Differences Between Rational and Geometric Base Points
Rational base points are defined over rational number fields and are crucial in arithmetic geometry for studying algebraic varieties with rational coordinates, whereas geometric base points correspond to points over algebraic closures, often facilitating universal constructions in algebraic geometry. The key difference lies in their field of definition: rational base points lie in fields with arithmetic significance, enabling number-theoretic properties, while geometric base points provide a more flexible framework by allowing extensions to algebraically closed fields. This distinction impacts how morphisms and fundamental groups are constructed, influencing the complexity and applications of the theories involved.
Role in Algebraic Geometry
Rational base points in algebraic geometry correspond to points defined over a specified base field, playing a crucial role in studying varieties with respect to field extensions and rationality properties. Geometric base points, defined over an algebraic closure of the base field, enable a more intrinsic analysis of the geometric structure and fundamental group of varieties independent of arithmetic constraints. Understanding the distinction between rational and geometric base points is essential for examining the interplay between arithmetic geometry and the intrinsic topology of algebraic varieties.
Applications in Fundamental Groups
Rational base points, defined over number fields or arithmetic schemes, provide a framework for studying the arithmetic fundamental group and its Galois actions, crucial in anabelian geometry and arithmetic algebraic geometry. Geometric base points, typically defined over algebraically closed fields such as the complex numbers, facilitate the analysis of the topological fundamental group and its monodromy representations in algebraic topology. Comparing these concepts enables deeper insights into the relationship between arithmetic and geometric fundamental groups, especially in the study of moduli spaces and etale coverings.
Impact on Galois Theory
Rational base points in algebraic geometry correspond to points defined over the base field, enabling direct application of Galois actions on their coordinates, which facilitates the study of arithmetic fundamental groups through rational coverings. Geometric base points, often chosen over algebraic closures, allow analysis of the full etale fundamental group, capturing more extensive monodromy and providing a refined understanding of the Galois representations associated with the scheme. The choice between rational and geometric base points critically impacts the decomposition of Galois groups and the interpretation of fiber functors in Galois categories, influencing the structure and behavior of fundamental groupoids in arithmetic geometry.
Examples Illustrating Each Type
Rational base points in algebraic geometry refer to points defined over a given field, such as the rational numbers \(\mathbb{Q}\), with examples like the point \((1,2)\) on the curve \(y = x^2\) over \(\mathbb{Q}\). Geometric base points involve algebraic closures of fields, for instance, the point \((\sqrt{2}, 2)\) on the same curve considered over \(\overline{\mathbb{Q}}\), the algebraic closure of \(\mathbb{Q}\). These examples distinguish the concept by showing a rational base point exists strictly within the original field, while geometric base points allow coordinates in larger algebraic extensions.
Choosing the Right Base Point: Considerations
Choosing the right base point involves evaluating the context of the problem and the properties of the coordinate system; a rational base point offers exact values suited for algebraic computations, while a geometric base point provides intuitive spatial understanding ideal for graphical interpretations. Considerations include the need for precision, the nature of transformations applied, and the complexity of calculations involved. Selecting between a rational or geometric base point directly affects accuracy, computational efficiency, and the clarity of geometric representations.
Conclusion: Implications and Further Reading
The distinction between rational base points and geometric base points significantly impacts algebraic geometry, influencing the study of varieties over different fields and their Galois actions. Understanding these concepts clarifies how field extensions affect point classification, offering deeper insights into rationality problems and arithmetic geometry. For further reading, exploring sources like Serre's "Galois Cohomology" and Hartshorne's "Algebraic Geometry" provides comprehensive frameworks on field base points and their mathematical implications.
Rational base point Infographic
 libterm.com
libterm.com