A CW complex is a topological space constructed by gluing cells of varying dimensions together in a specific way, enabling a combinatorial approach to studying topology. It provides a flexible framework to analyze spaces by breaking them down into basic building blocks, making it easier to compute homotopy and homology groups. Explore this article to understand the fundamentals and applications of CW complexes in modern topology.
Table of Comparison
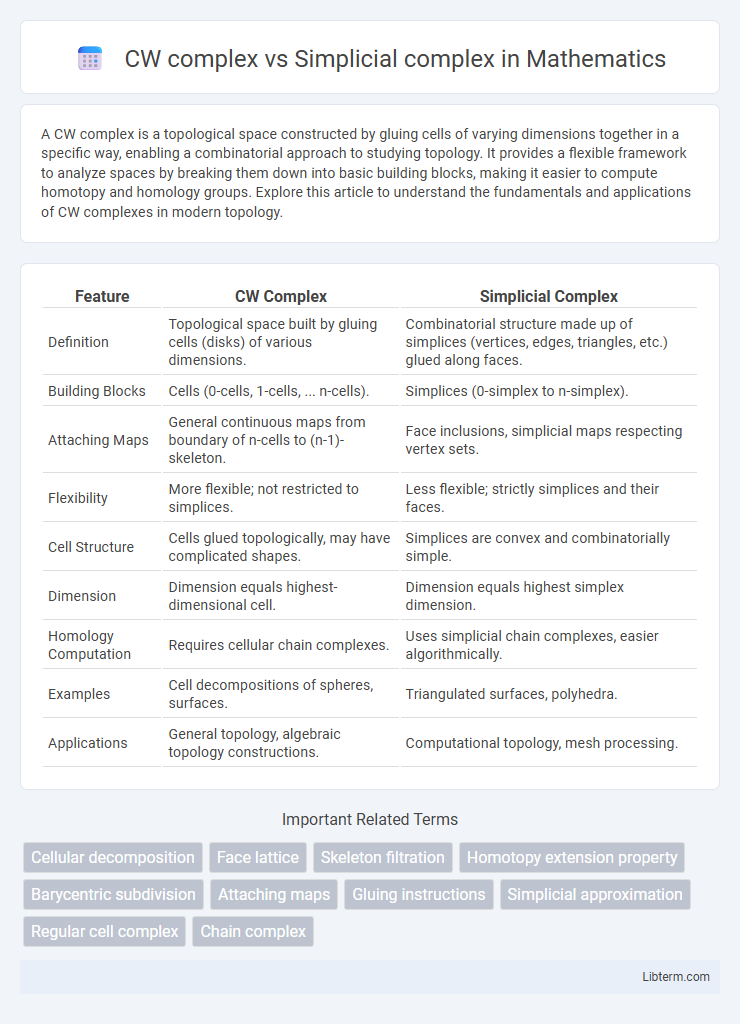
| Feature | CW Complex | Simplicial Complex |
|---|---|---|
| Definition | Topological space built by gluing cells (disks) of various dimensions. | Combinatorial structure made up of simplices (vertices, edges, triangles, etc.) glued along faces. |
| Building Blocks | Cells (0-cells, 1-cells, ... n-cells). | Simplices (0-simplex to n-simplex). |
| Attaching Maps | General continuous maps from boundary of n-cells to (n-1)-skeleton. | Face inclusions, simplicial maps respecting vertex sets. |
| Flexibility | More flexible; not restricted to simplices. | Less flexible; strictly simplices and their faces. |
| Cell Structure | Cells glued topologically, may have complicated shapes. | Simplices are convex and combinatorially simple. |
| Dimension | Dimension equals highest-dimensional cell. | Dimension equals highest simplex dimension. |
| Homology Computation | Requires cellular chain complexes. | Uses simplicial chain complexes, easier algorithmically. |
| Examples | Cell decompositions of spheres, surfaces. | Triangulated surfaces, polyhedra. |
| Applications | General topology, algebraic topology constructions. | Computational topology, mesh processing. |
Introduction to Topological Complexes
CW complexes provide a flexible framework for constructing topological spaces by iteratively attaching cells of increasing dimension, allowing for efficient handling of complex shapes. Simplicial complexes consist of simplices--points, line segments, triangles, and higher-dimensional analogs--glued together along their faces, offering a combinatorial approach to topology. CW complexes generalize simplicial complexes by permitting more general cell attachments, making them particularly useful in algebraic topology for studying homotopy and homology theories.
Defining Simplicial Complexes
A simplicial complex is a collection of simplices--points, line segments, triangles, and their higher-dimensional counterparts--that are combined in a way such that every face of a simplex is also included in the complex and the intersection of any two simplices is either empty or a shared face. This definition ensures a combinatorial structure built from finite sets of vertices and their subsets, facilitating computational and topological analysis. Unlike CW complexes, simplicial complexes have a rigid geometric realization with explicit simplices, making them fundamental in algebraic topology and computational geometry.
Defining CW Complexes
CW complexes are topological spaces constructed by inductively attaching cells of increasing dimension via continuous maps from the boundary spheres of n-disks, creating a cellular structure ideal for homotopy theory. Each n-cell is glued to the (n-1)-skeleton through characteristic maps, ensuring closure-finiteness and the weak topology conditions that distinguish CW complexes from simplicial complexes. Unlike simplicial complexes, which rely on simplices and combinatorial data, CW complexes provide more flexibility for handling complex topological spaces by using general cells rather than strictly simplices.
Construction Methods: Simplicial vs CW Complexes
Simplicial complexes are constructed by gluing simplices such as points, line segments, triangles, and their higher-dimensional counterparts along their faces in a combinatorial manner, ensuring that each face of a simplex belongs to the complex. CW complexes are built by inductively attaching cells (disks of various dimensions) via continuous maps from their boundary spheres to the existing complex, allowing more flexible and efficient representation of topological spaces. The construction of simplicial complexes is often more rigid and combinatorial, while CW complexes offer greater adaptability in capturing topological features with fewer cells.
Examples of Simplicial Complexes
Simplicial complexes are constructed using simplexes such as vertices, edges, triangles, and higher-dimensional analogs that are glued together along shared faces, with the boundary of each simplex forming a union of lower-dimensional simplexes. Common examples include triangulated surfaces like the tetrahedron, triangulations of polygons, and complexes formed by subdividing spaces into simplexes for computational topology. In contrast, CW complexes allow more general attaching maps and cells of arbitrary shape, providing greater flexibility in modeling topological spaces that may not admit a pure simplicial decomposition.
Examples of CW Complexes
Examples of CW complexes include the n-dimensional sphere \(S^n\), constructed by attaching an n-cell to a point, and the torus, formed by gluing two 1-cells and a 2-cell along their boundaries. Unlike simplicial complexes, CW complexes allow cells to be attached using continuous maps, enabling more flexible and efficient decompositions of topological spaces such as the Mobius strip and projective spaces. These structures capture essential topological features while minimizing combinatorial complexity compared to simplicial complexes.
Key Differences Between Simplicial and CW Complexes
Simplicial complexes are built from simplices (points, line segments, triangles, and their higher-dimensional analogs) glued together along faces, enforcing strict combinatorial rules that facilitate computational ease and explicit geometric representation. CW complexes, in contrast, are constructed inductively by attaching cells of increasing dimension via continuous maps, offering greater flexibility to model spaces with less rigid combinatorial constraints and often simplifying homotopy-theoretic analysis. While simplicial complexes are favored for their combinatorial clarity and algorithmic applications, CW complexes excel in algebraic topology for efficiently representing complex spaces and enabling tools like cellular homology.
Applications in Algebraic Topology
CW complexes and simplicial complexes serve as foundational structures in algebraic topology for decomposing spaces into manageable pieces to compute homotopy and homology groups. CW complexes offer greater flexibility and generality than simplicial complexes by allowing cells to attach via continuous maps, making them ideal for modeling complex topological spaces such as classifying spaces and spectral sequences. Simplicial complexes, with their combinatorial nature, facilitate explicit computations and algorithmic approaches in persistent homology and topological data analysis.
Advantages and Limitations of Each Complex
CW complexes allow for greater flexibility in constructing topological spaces by attaching cells of varying dimensions, making them ideal for studying complex spaces with fewer restrictions on cell shape. Simplicial complexes offer a combinatorial advantage with their simplex-based structure, facilitating algorithmic manipulation and computation in computational topology. However, CW complexes can be more abstract and harder to handle computationally, while simplicial complexes may require a high number of simplices to model complicated spaces accurately, leading to scalability issues.
Choosing Between CW and Simplicial Complexes
Choosing between CW complexes and simplicial complexes depends on the topological properties and computational goals of the space under study. CW complexes offer flexibility through their cell attachment maps, allowing more general and efficient modeling of spaces with complex structures, whereas simplicial complexes provide a combinatorial and algorithm-friendly framework ideal for computational topology and discrete geometry. Researchers prioritize CW complexes when dealing with homotopy and homology theories requiring fewer but more adaptable building blocks, while simplicial complexes are favored for their straightforward simplicial maps and mesh representations in applications like computer graphics and data analysis.
CW complex Infographic
 libterm.com
libterm.com