Homomorphism is a fundamental concept in algebra that describes a structure-preserving map between two algebraic systems such as groups, rings, or vector spaces. It ensures operations in one system correspond consistently to operations in another, maintaining the integrity of their algebraic properties. Discover how understanding homomorphism can enhance your grasp of mathematics by exploring the detailed insights in the rest of this article.
Table of Comparison
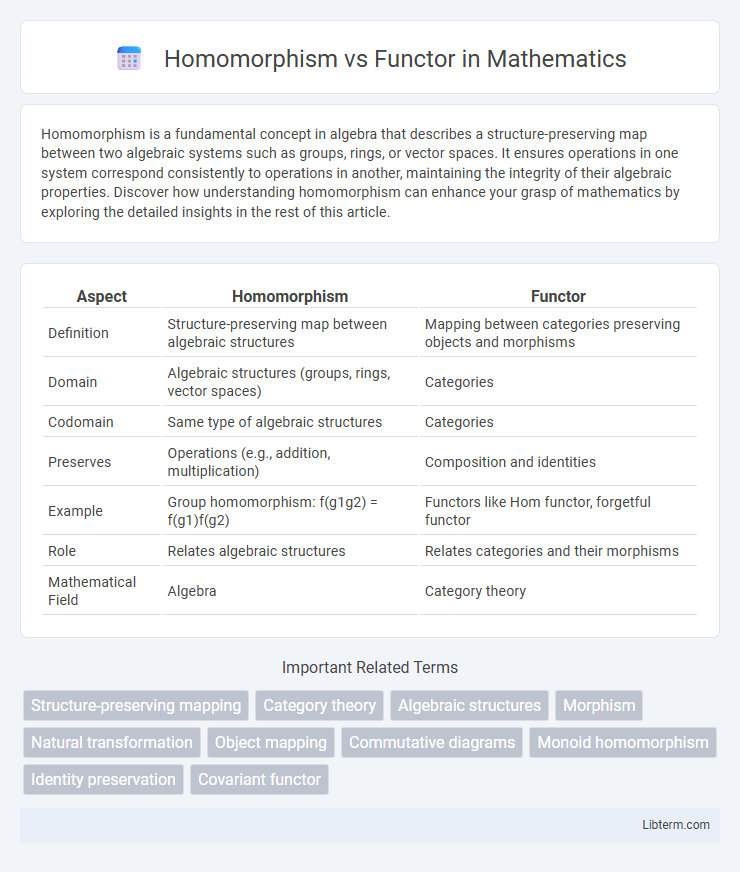
| Aspect | Homomorphism | Functor |
|---|---|---|
| Definition | Structure-preserving map between algebraic structures | Mapping between categories preserving objects and morphisms |
| Domain | Algebraic structures (groups, rings, vector spaces) | Categories |
| Codomain | Same type of algebraic structures | Categories |
| Preserves | Operations (e.g., addition, multiplication) | Composition and identities |
| Example | Group homomorphism: f(g1g2) = f(g1)f(g2) | Functors like Hom functor, forgetful functor |
| Role | Relates algebraic structures | Relates categories and their morphisms |
| Mathematical Field | Algebra | Category theory |
Introduction to Homomorphism and Functor
A homomorphism is a structure-preserving map between two algebraic structures, such as groups, rings, or vector spaces, maintaining operations like addition or multiplication. Functors generalize this concept within category theory by mapping objects and morphisms from one category to another, preserving the compositional and identity structure. Understanding homomorphisms as specific cases of functors highlights the abstraction and unification of mathematical structures across different contexts.
Defining Homomorphism in Abstract Algebra
Homomorphism in abstract algebra is a structure-preserving map between two algebraic structures, such as groups, rings, or vector spaces, that respects the operations defined on those structures. It satisfies the property f(x * y) = f(x) *' f(y), where * and *' denote the binary operations in the domain and codomain respectively. Unlike functors, which map between categories preserving objects and morphisms, homomorphisms focus on preserving algebraic operations within a specific type of algebraic system.
Understanding Functor in Category Theory
A functor in category theory is a mapping between categories that preserves the structure of objects and morphisms, ensuring compositions and identities correspond. Unlike a homomorphism, which maps between algebraic structures like groups or rings, a functor operates at a higher level of abstraction, relating entire categories rather than individual elements. Understanding functors is crucial for studying connections between mathematical frameworks and enables the translation of concepts across different categorical contexts.
Key Differences Between Homomorphism and Functor
Homomorphisms are structure-preserving maps between algebraic structures such as groups, rings, or vector spaces, ensuring operations like addition or multiplication commute with the map. Functors operate between categories, mapping objects to objects and morphisms to morphisms while preserving identity morphisms and composition, thus providing a higher-level abstraction. Key differences include their domains--homomorphisms act on algebraic structures, functors on categories--and their role in connecting elements versus entire morphisms and objects within categorical contexts.
Structural Preservation: Homomorphism vs Functor
Homomorphisms preserve the algebraic structure between two algebraic systems by ensuring that operations in the source system correspond directly to operations in the target system. Functors extend this concept to category theory by mapping objects and morphisms between categories while preserving composition and identity morphisms, thus maintaining the categorical structure. Unlike homomorphisms that focus on algebraic operations, functors guarantee structural preservation across more abstract mathematical frameworks.
Applications of Homomorphism
Homomorphisms play a crucial role in algebraic structures by preserving operations between groups, rings, or vector spaces, enabling the transfer of properties and simplification of complex problems. They are extensively applied in cryptography for constructing secure encryption schemes and in coding theory to design error-correcting codes. Additionally, homomorphisms facilitate the study of symmetry in mathematical physics and enable efficient computation in computer algebra systems.
Applications of Functor
Functors are widely used in functional programming to map between categories while preserving structure, enabling robust data transformations and modular code design. They facilitate operations on complex data types such as lists, trees, and option types by applying functions uniformly within a computational context. Unlike homomorphisms, which primarily focus on structure-preserving maps between algebraic structures, functors provide a more generalized framework applicable to a broad range of programming paradigms and category theory concepts.
Real-World Examples: Homomorphism vs Functor
Homomorphisms appear in algebraic structures such as group theory where a function preserves operations, for example, mapping integers under addition to even integers maintaining the addition operation. Functors operate within category theory, linking categories by mapping objects and morphisms while preserving composition and identity, seen in programming languages like Haskell where functors map data types to other data types consistently. Real-world applications of homomorphisms include cryptographic functions ensuring structured data transformation, whereas functors facilitate modular software design by enabling generic programming and reusable code patterns.
Homomorphism and Functor in Modern Mathematics
Homomorphisms are structure-preserving maps between algebraic structures such as groups, rings, or vector spaces, playing a fundamental role in modern algebra by enabling the comparison and classification of these structures. Functors generalize this concept to category theory, acting as mappings between categories that preserve the composition of morphisms and identity morphisms, thus enabling the study of mathematical structures and their relationships at a higher level of abstraction. Both homomorphisms and functors are essential in modern mathematics for understanding and transferring properties between different mathematical contexts, underpinning advances in algebra, topology, and other fields.
Conclusion: Selecting the Right Concept
Choosing between homomorphisms and functors depends on the mathematical context and abstraction level required. Homomorphisms map between algebraic structures preserving operations, ideal for concrete algebraic problems. Functors operate between categories, capturing structure-preserving relationships in a broader, more abstract framework, making them essential in category theory and advanced mathematical fields.
Homomorphism Infographic
 libterm.com
libterm.com