Linear order organizes elements in a sequential manner, ensuring each item follows a specific predecessor and precedes a successor. This structure is essential in computing, mathematics, and everyday scheduling to maintain clarity and consistency. Explore the rest of the article to discover practical applications and benefits of linear order in various fields.
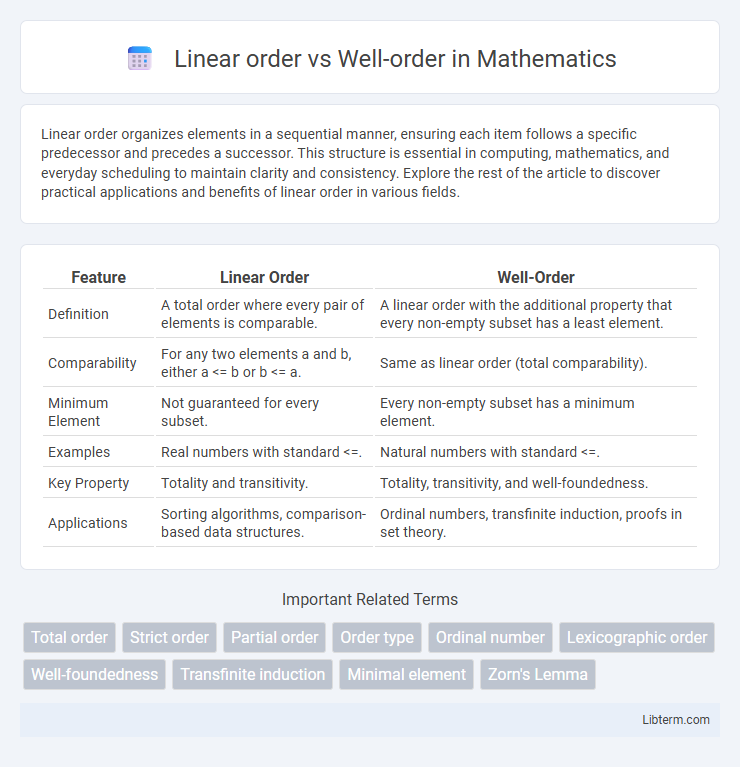
Table of Comparison
| Feature | Linear Order | Well-Order |
|---|---|---|
| Definition | A total order where every pair of elements is comparable. | A linear order with the additional property that every non-empty subset has a least element. |
| Comparability | For any two elements a and b, either a <= b or b <= a. | Same as linear order (total comparability). |
| Minimum Element | Not guaranteed for every subset. | Every non-empty subset has a minimum element. |
| Examples | Real numbers with standard <=. | Natural numbers with standard <=. |
| Key Property | Totality and transitivity. | Totality, transitivity, and well-foundedness. |
| Applications | Sorting algorithms, comparison-based data structures. | Ordinal numbers, transfinite induction, proofs in set theory. |
Introduction to Linear Order and Well-Order
Linear order is a binary relation on a set where every pair of elements is comparable, meaning for any two elements a and b, either a <= b or b <= a holds. Well-order is a stronger form of linear order that requires every non-empty subset to have a least element, ensuring no infinite descending chains exist. Understanding the distinction between linear order and well-order is fundamental in set theory and order theory, particularly in analyzing structures like ordinals and the hierarchy of infinities.
Defining Linear Order: Key Concepts
Linear order, also known as total order, is a binary relation on a set that is transitive, antisymmetric, and connex, meaning every pair of elements is comparable. In a linear order, for any elements a and b, either a <= b or b <= a holds, establishing a complete sequence without gaps. This concept contrasts with well-ordering by not requiring every non-empty subset to have a least element, allowing infinite descending chains.
Understanding Well-Order: Essential Features
A well-order is a special type of linear order in which every non-empty subset has a least element, ensuring no infinite descending chains exist. This property distinguishes well-orders from general linear orders, as it guarantees a clear minimal element for any subset, facilitating inductive arguments and recursive definitions. Well-orders play a crucial role in set theory and ordinal analysis due to their foundational structure in ordering principles.
Fundamental Differences Between Linear Order and Well-Order
Linear order is a binary relation that arranges elements in a sequence where every pair is comparable, allowing the possibility of infinite descending chains or subsets without a least element. Well-order strengthens this structure by requiring every non-empty subset to have a least element, eliminating infinite descending sequences and ensuring minimal elements always exist. The fundamental difference lies in well-order's guarantee of a least element in all subsets, which is crucial for transfinite induction and ordinal number theory.
Mathematical Examples of Linear Orders
Linear orders include familiar sets like the real numbers (R) under the usual <= relation, where any two elements are comparable, but not all subsets have least elements. The set of integers (Z) with the standard order is a linear order that is not well-ordered since infinite decreasing sequences exist without minimal elements. In contrast, natural numbers (N) are both linearly ordered and well-ordered, illustrating the key difference that well-orders require every non-empty subset to have a least element.
Illustrative Examples of Well-Orders
A well-order is a linear order with the additional property that every non-empty subset has a least element, exemplified by the natural numbers \(\mathbb{N}\) under the usual order. The ordinal numbers provide a broad class of well-orders, where finite ordinals correspond to natural numbers and infinite ordinals extend beyond them, such as \(\omega\), the first infinite ordinal. Unlike the real numbers with their standard order, which lack a least element in subsets like open intervals, well-orders ensure a minimal element exists, enabling transfinite induction and recursion.
Importance of the Well-Ordering Principle
The Well-Ordering Principle states that every non-empty set of positive integers contains a least element, a concept essential to proofs by induction and foundational number theory. Unlike linear orders, which require every pair of elements to be comparable, well-orders impose a stronger condition ensuring no infinite descending chains, facilitating robust structural analysis. This principle underpins algorithms, model theory, and ordinal numbers, highlighting its critical role in both theoretical and applied mathematics.
Applications of Linear Order and Well-Order in Mathematics
Linear order structures enable the organization of sets where every pair of elements is comparable, facilitating algorithms in sorting, optimization, and scheduling problems. Well-ordering extends linear orders by ensuring every non-empty subset has a least element, proving essential in transfinite induction and ordinal number theory. These properties underpin foundational techniques in proof theory, model theory, and the classification of mathematical objects.
Comparing Properties and Implications
Linear orders require every pair of elements to be comparable, ensuring a total ordering, while well-orders extend this by demanding every non-empty subset have a least element, introducing minimality properties. Well-orders guarantee the applicability of transfinite induction and recursive definitions, essential in set theory and ordinal analysis, whereas linear orders may have subsets with no minimal element, limiting such techniques. The absence of infinite descending chains in well-orders contrasts with linear orders, impacting their structural complexity and the types of order-preserving functions they admit.
Summary: Choosing Between Linear Order and Well-Order
Linear orders arrange elements so every pair is comparable, enabling straightforward comparisons without guaranteeing minimal elements in every subset. Well-orders extend linear orders by ensuring every non-empty subset possesses a least element, crucial for defining transfinite induction and ordinal numbers. Selecting between linear and well-orders depends on whether minimal element existence is required, with well-orders preferred for rigorous hierarchical structures and proofs in set theory.
Linear order Infographic
 libterm.com
libterm.com