Euclidean geometry focuses on the study of points, lines, and shapes based on the axioms established by the ancient Greek mathematician Euclid. This branch of mathematics forms the foundation for understanding spatial relationships and properties in a flat, two-dimensional plane. Explore the rest of the article to deepen your knowledge of Euclidean principles and their applications.
Table of Comparison
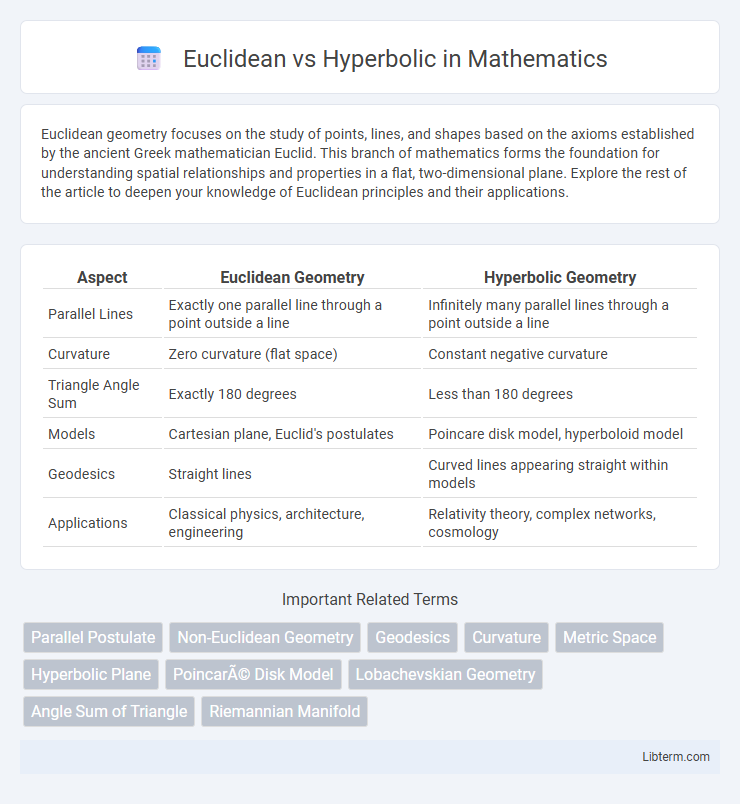
| Aspect | Euclidean Geometry | Hyperbolic Geometry |
|---|---|---|
| Parallel Lines | Exactly one parallel line through a point outside a line | Infinitely many parallel lines through a point outside a line |
| Curvature | Zero curvature (flat space) | Constant negative curvature |
| Triangle Angle Sum | Exactly 180 degrees | Less than 180 degrees |
| Models | Cartesian plane, Euclid's postulates | Poincare disk model, hyperboloid model |
| Geodesics | Straight lines | Curved lines appearing straight within models |
| Applications | Classical physics, architecture, engineering | Relativity theory, complex networks, cosmology |
Introduction to Euclidean and Hyperbolic Geometry
Euclidean geometry, founded on the postulates of Euclid, describes flat spaces with parallel lines that never intersect, forming the basis for classical geometry taught in schools. Hyperbolic geometry, a non-Euclidean geometry developed by Lobachevsky and Bolyai, explores curved spaces where parallel lines diverge and the sum of angles in a triangle is less than 180 degrees. These geometries fundamentally differ in their treatment of parallelism and curvature, influencing fields like cosmology and theoretical physics.
Historical Development of Geometric Systems
The historical development of geometric systems began with Euclidean geometry, formalized by Euclid around 300 BCE, which dominated mathematical thought for over two millennia with its axiomatic approach and the parallel postulate. Hyperbolic geometry emerged in the 19th century through the work of mathematicians like Nikolai Lobachevsky and Janos Bolyai, who independently challenged Euclid's parallel postulate and introduced consistent models where multiple parallel lines pass through a point. This paradigm shift expanded the scope of geometry, influencing modern mathematics, physics, and our understanding of space.
Fundamental Axioms: Euclidean vs Hyperbolic
Euclidean geometry is based on five fundamental axioms, notably the parallel postulate stating that through a point not on a line, exactly one parallel line exists. Hyperbolic geometry modifies this by allowing infinitely many parallel lines through that point, violating Euclid's parallel postulate. This key axiom difference leads to distinct properties in shapes, angles, and distances between Euclidean and hyperbolic spaces.
Parallel Postulate: The Key Difference
The key difference between Euclidean and Hyperbolic geometry lies in the Parallel Postulate; Euclidean geometry states that through a point not on a line, exactly one parallel line can be drawn, while Hyperbolic geometry asserts that infinitely many parallel lines exist through that point. This fundamental divergence affects the behavior of lines, angles, and shapes, leading to distinct geometric properties and applications in fields like cosmology and complex network analysis. Understanding this difference reveals the nature of space curvature, where Euclidean geometry assumes flat space, and Hyperbolic geometry describes negatively curved space.
Visualization and Representation of Geometries
Euclidean geometry represents shapes and spaces using flat planes and parallel lines with consistent distances and angles, making it ideal for straightforward visualization and standard spatial reasoning. Hyperbolic geometry, characterized by its constant negative curvature and non-parallel lines that diverge, requires specialized models such as the Poincare disk or the hyperboloid model for effective visualization and accurate representation. These models preserve angles but distort distances, allowing the complex structure of hyperbolic spaces to be intuitively visualized despite the curvature differences from Euclidean spaces.
Distance and Angle Measurements
Euclidean geometry defines distance using the Pythagorean theorem, where the distance between two points is the length of the straight line segment joining them, and angles are measured using standard Euclidean angle definitions based on dot products. Hyperbolic geometry, however, utilizes the hyperbolic metric, characterized by distance calculations that involve hyperbolic functions such as sinh and cosh, causing distance to grow exponentially as points move further apart. Angles in hyperbolic space preserve their measure through hyperbolic isometries, but the sum of angles in hyperbolic triangles is always less than 180 degrees, contrasting with Euclidean triangles where the sum equals 180 degrees.
Applications in Mathematics and Physics
Euclidean geometry underpins classical mechanics, computer graphics, and solving problems involving flat space, while hyperbolic geometry plays a crucial role in relativity theory, modeling spacetime curvature, and complex network analysis. In mathematics, Euclidean spaces facilitate vector calculus and linear algebra applications, whereas hyperbolic spaces support non-Euclidean trigonometry and group theory investigations. Both geometries enable advancements in quantum field theory and cosmology by providing frameworks for understanding different spatial curvatures.
Real-World Examples and Models
Euclidean geometry governs everyday objects and architectural structures, such as city layouts and engineering designs, where parallel lines never meet and shapes maintain constant angles. Hyperbolic geometry models complex, large-scale networks like the internet and social graphs, capturing exponential growth and hierarchical relationships with curvature that diverges from flat surfaces. Real-world applications include navigation systems using Euclidean metrics for precise distances and biological neural mapping leveraging hyperbolic embeddings for efficient hierarchical representation.
Advantages and Limitations of Each Geometry
Euclidean geometry excels in providing intuitive concepts and accurate measurements on flat surfaces, making it ideal for everyday applications and classical physics. Hyperbolic geometry offers advantages in modeling complex, negatively curved spaces, such as in relativity theory and certain network structures, but its non-Euclidean nature can complicate visualization and computation. While Euclidean geometry faces limitations when applied to curved spaces, hyperbolic geometry may not align well with conventional intuition, posing challenges in practical implementation.
Conclusion: Comparing Euclidean and Hyperbolic Spaces
Euclidean space is characterized by flat geometry where parallel lines never intersect, while hyperbolic space exhibits constant negative curvature allowing many parallel lines through a point outside a given line. Hyperbolic geometry enables more efficient representations of hierarchical and tree-like structures due to its exponential growth properties. For applications in complex networks and data embedding, hyperbolic spaces often outperform Euclidean spaces by preserving relational distances more accurately.
Euclidean Infographic
 libterm.com
libterm.com