A projective module is a type of module in algebra that has the property of lifting homomorphisms through surjections, making it a direct summand of a free module. This characteristic simplifies complex module structures and plays a crucial role in homological algebra and module theory. Explore the article to deepen your understanding of projective modules and their applications.
Table of Comparison
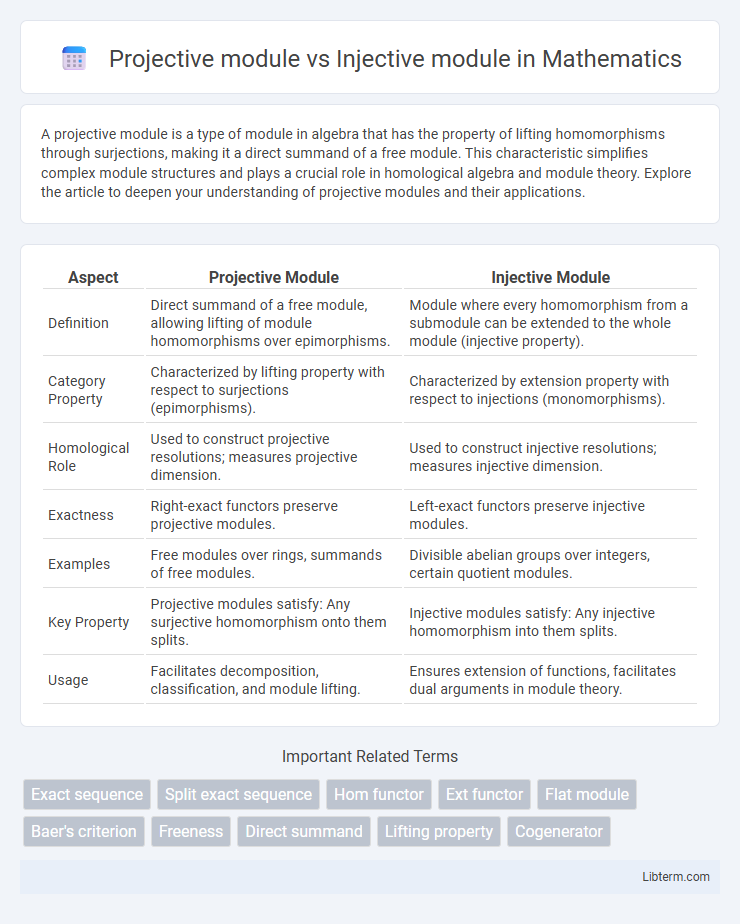
| Aspect | Projective Module | Injective Module |
|---|---|---|
| Definition | Direct summand of a free module, allowing lifting of module homomorphisms over epimorphisms. | Module where every homomorphism from a submodule can be extended to the whole module (injective property). |
| Category Property | Characterized by lifting property with respect to surjections (epimorphisms). | Characterized by extension property with respect to injections (monomorphisms). |
| Homological Role | Used to construct projective resolutions; measures projective dimension. | Used to construct injective resolutions; measures injective dimension. |
| Exactness | Right-exact functors preserve projective modules. | Left-exact functors preserve injective modules. |
| Examples | Free modules over rings, summands of free modules. | Divisible abelian groups over integers, certain quotient modules. |
| Key Property | Projective modules satisfy: Any surjective homomorphism onto them splits. | Injective modules satisfy: Any injective homomorphism into them splits. |
| Usage | Facilitates decomposition, classification, and module lifting. | Ensures extension of functions, facilitates dual arguments in module theory. |
Introduction to Projective and Injective Modules
Projective modules are characterized by their property of lifting homomorphisms through surjective module maps, making them direct summands of free modules and essential in constructing projective resolutions. Injective modules, defined by the extension property of homomorphisms from submodules, serve as targets for embedding modules to form injective resolutions critical in homological algebra. Both projective and injective modules play fundamental roles in the study of module theory, enabling deeper analysis of exact sequences and homological dimensions.
Definitions: What Are Projective Modules?
Projective modules are modules with the property that every surjective module homomorphism onto them splits, meaning they can be lifted through surjections. Formally, a module \(P\) is projective if for every surjective homomorphism \(f: M \to N\) and any homomorphism \(g: P \to N\), there exists a homomorphism \(h: P \to M\) such that \(f \circ h = g\). This lifting property characterizes projective modules as direct summands of free modules, enabling them to facilitate exact sequences in homological algebra.
Definitions: What Are Injective Modules?
Injective modules are modules over a ring that possess the property allowing any homomorphism defined on a submodule to extend to the entire module, making them essential for studying module extensions and exact sequences. Formally, a module \( E \) is injective if for every inclusion \( A \subseteq B \) and every module homomorphism \( f: A \to E \), there exists an extension \( \tilde{f}: B \to E \) such that \( \tilde{f}|_A = f \). This extension property characterizes injective modules and distinguishes them from projective modules, which have a lifting property against surjections instead.
Key Properties of Projective Modules
Projective modules are characterized by their ability to lift module homomorphisms through surjections, ensuring the existence of a module homomorphism that makes a given diagram commute. They are direct summands of free modules, which guarantees that projective modules share many of the desirable properties of free modules, such as being flat and preserving exactness in sequences. In contrast, injective modules are defined by their extension property, allowing any module homomorphism defined on a submodule to extend to the entire module.
Key Properties of Injective Modules
Injective modules are characterized by their ability to extend homomorphisms from submodules to the entire module, making them essential in solving extension problems in module theory. These modules are closed under taking direct sums and direct products, and every module can be embedded into an injective module, demonstrating their role as injective hulls. Key properties include Baer's criterion for injectivity, which provides a practical test for injectivity by examining the extension of homomorphisms from ideals to the entire ring.
Characterizations and Examples
Projective modules are characterized by their property that every surjective module homomorphism onto them splits, making them direct summands of free modules; for example, free modules over a ring are projective. Injective modules are defined by the property that every injective module homomorphism from them splits, equivalently they satisfy the Baer criterion; an example includes the module of rational numbers \(\mathbb{Q}\) as an injective \(\mathbb{Z}\)-module. While projective modules facilitate lifting properties in exact sequences, injective modules support extension properties, making both fundamental in homological algebra and module theory.
Categorical Perspectives: Projectivity vs Injectivity
Projective modules correspond to objects with lifting properties that facilitate factorization through epimorphisms, reflecting their role as retracts of free modules in the category of modules. Injective modules, dually, possess extension properties that allow morphisms defined on submodules to extend over the entire module, serving as essential extensions in categorical terms. This duality highlights the fundamental correspondence between projectivity and injectivity in homological algebra, characterizing them via universal properties in abelian categories.
Homological Relationships and Exact Sequences
Projective modules are characterized by the property that the functor Hom(P, -) is exact, preserving exact sequences in the second argument, which ensures the lifting of morphisms through surjections. Injective modules satisfy that the functor Hom(-, I) is exact, preserving exact sequences in the first argument, allowing extensions of morphisms from submodules. These dual properties imply projective modules facilitate splitting of surjective maps, while injective modules enable the extension of maps, both playing crucial roles in constructing exact sequences in homological algebra.
Applications in Algebra and Module Theory
Projective modules facilitate the construction of free resolutions, crucial for computing Ext and Tor functors in homological algebra, enabling the classification of modules over rings. Injective modules play a key role in module theory by allowing the extension of homomorphisms and simplifying the study of exact sequences through injective resolutions, which are essential for derived functor calculations and cohomological methods. Both module types underpin many structural results in algebra, including decomposition theorems and duality principles in representation theory and category theory.
Summary: Comparing Projective and Injective Modules
Projective modules are characterized by their lifting property, allowing homomorphisms to be extended along surjections, which facilitates constructing module decompositions and enables direct sum decomposability. Injective modules possess the extension property, ensuring homomorphisms defined on submodules extend over the entire module, making them essential in resolving exact sequences and cohomological contexts. Both projective and injective modules serve as fundamental tools in homological algebra, crucial for studying module categories, with projectives focusing on lifting structures and injectives on extending functions.
Projective module Infographic
 libterm.com
libterm.com