Retraction is a critical process in academic publishing that ensures the integrity and accuracy of the scientific record by formally withdrawing published papers that contain significant errors or ethical issues. Understanding the reasons and implications of retractions can help you navigate research literature more confidently and avoid misinformation. Explore the rest of the article to learn how retractions impact scholarly communication and what steps you can take when encountering retracted work.
Table of Comparison
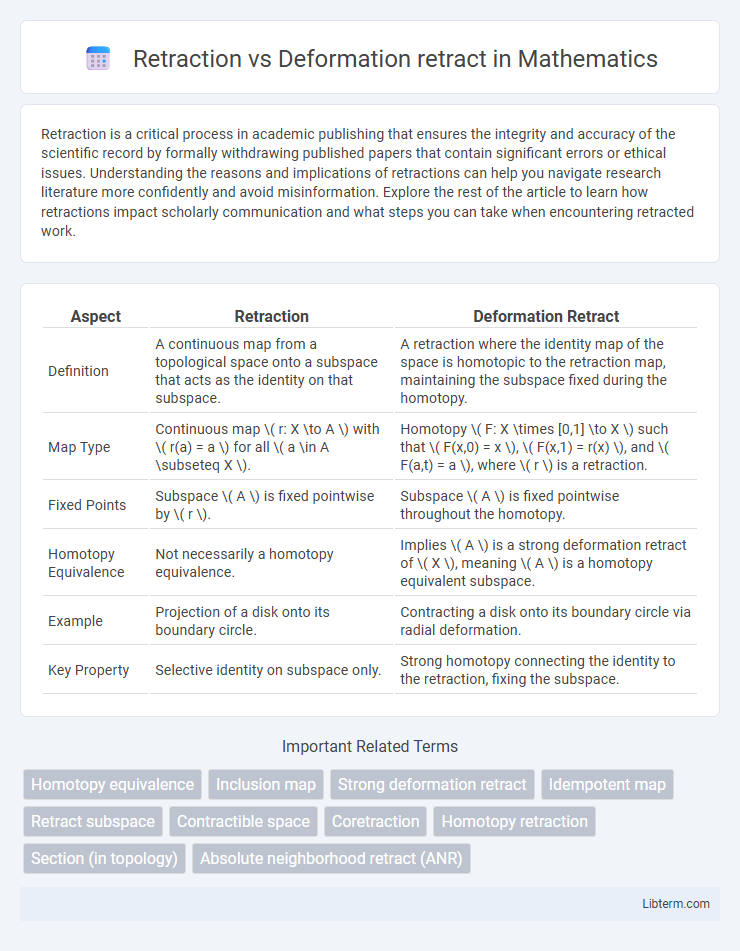
| Aspect | Retraction | Deformation Retract |
|---|---|---|
| Definition | A continuous map from a topological space onto a subspace that acts as the identity on that subspace. | A retraction where the identity map of the space is homotopic to the retraction map, maintaining the subspace fixed during the homotopy. |
| Map Type | Continuous map \( r: X \to A \) with \( r(a) = a \) for all \( a \in A \subseteq X \). | Homotopy \( F: X \times [0,1] \to X \) such that \( F(x,0) = x \), \( F(x,1) = r(x) \), and \( F(a,t) = a \), where \( r \) is a retraction. |
| Fixed Points | Subspace \( A \) is fixed pointwise by \( r \). | Subspace \( A \) is fixed pointwise throughout the homotopy. |
| Homotopy Equivalence | Not necessarily a homotopy equivalence. | Implies \( A \) is a strong deformation retract of \( X \), meaning \( A \) is a homotopy equivalent subspace. |
| Example | Projection of a disk onto its boundary circle. | Contracting a disk onto its boundary circle via radial deformation. |
| Key Property | Selective identity on subspace only. | Strong homotopy connecting the identity to the retraction, fixing the subspace. |
Introduction to Retraction and Deformation Retract
A retraction is a continuous mapping from a topological space onto a subspace that leaves points of the subspace fixed, serving as an identity map restricted to that subspace. A deformation retract refines this concept by providing a homotopy between the identity map on the entire space and the retraction, effectively shrinking the space onto the subspace while preserving its homotopy type. Both concepts play crucial roles in algebraic topology, particularly in simplifying complex spaces while retaining essential topological properties.
Definitions: Retraction Explained
A retraction is a continuous map from a topological space X onto a subspace A that leaves every point of A fixed, effectively "retracting" X onto A without altering A itself. This concept requires the existence of a retraction function r: X - A such that r(a) = a for all a in A, preserving the identity on A. Retractions play a crucial role in topology by facilitating deformation and simplification of spaces while maintaining essential subspace structure.
Understanding Deformation Retract
A deformation retract is a homotopy between a topological space and a subspace that continuously shrinks the entire space onto the subspace while keeping the subspace fixed. Unlike a simple retraction, which is just a continuous map from the space onto the subspace that acts as the identity on the subspace, a deformation retract provides a stronger condition by specifying this homotopy. Understanding deformation retracts is crucial in algebraic topology because they preserve homotopy type and allow simplifications of spaces without altering their fundamental group or homological properties.
Key Differences Between Retraction and Deformation Retract
Retraction is a continuous map from a topological space X onto a subspace A that leaves points of A fixed, whereas a deformation retract is a homotopy that continuously shrinks X onto A while keeping A fixed throughout the process. A key difference lies in that every deformation retract is a retraction, but not all retractions are deformation retracts because deformation retracts require a homotopy equivalence between X and A. Deformation retraction preserves the homotopy type of the subspace, making it a stronger condition than mere retraction.
Topological Foundations and Properties
Retraction is a continuous mapping from a topological space onto a subspace that leaves the points of that subspace fixed, ensuring the subspace is a deformation retract if it can be continuously shrunk within the space through a homotopy that fixes the subspace pointwise. Deformation retracts preserve homotopy type and induce isomorphisms in homotopy groups, making them foundational in algebraic topology for simplifying spaces while retaining essential topological properties. These concepts underscore fundamental topological invariants and are crucial in studying homotopy equivalences and the structure of spaces.
Examples of Retraction in Topology
A retraction is a continuous map from a topological space onto a subspace that leaves the points of that subspace fixed, with classic examples including the deformation of a disk onto its boundary circle or a cylinder onto one of its circular edges. The retraction from a closed disk to its boundary circle S1 is a fundamental example illustrating how the interior points are "retracted" onto the perimeter without altering the boundary points. Retracting a solid torus to a circle within it exemplifies retraction that is not necessarily a deformation retract, as it does not require a homotopy through embeddings preserving the subspace pointwise at all times.
Examples of Deformation Retracts
A classic example of a deformation retract is the circle \( S^1 \) being a deformation retract of the punctured plane \( \mathbb{R}^2 \setminus \{0\} \), where the space continuously shrinks onto the circle without cutting or gluing. Another fundamental example is the inclusion of a subspace \( X \) in a topological space \( Y \), such as a disk \( D^2 \) deformation retracting to its boundary circle \( S^1 \), highlighting how deformation retracts preserve homotopy type while retracts alone need not. The strong deformation retract of a solid torus onto its core circle showcases how these mappings maintain essential topological features by allowing homotopies that contract the space onto a subspace.
Importance in Homotopy Theory
Retraction and deformation retract serve as fundamental concepts in homotopy theory by providing tools to simplify complex spaces while preserving their essential topological properties. A deformation retract allows a continuous deformation of a space onto a subspace, ensuring that the inclusion map and retraction are homotopy inverses, which preserves homotopy type and facilitates computation of fundamental groups and homotopy groups. Retraction alone, lacking homotopy equivalence, is less powerful in applications of homotopy theory but remains crucial in defining fixed point properties and retraction theorems.
Applications in Algebraic Topology
Retraction and deformation retract play crucial roles in algebraic topology by enabling simplification of complex spaces while preserving topological properties. Retractions allow defining subspace invariants by mapping spaces onto subspaces continuously, often utilized in fixed point theorems and homotopy theory. Deformation retracts offer stronger homotopy equivalences that facilitate computation of fundamental groups and homology groups by reducing spaces to simpler, homotopy-equivalent subspaces.
Conclusion: Comparing Retraction and Deformation Retract
Retraction is a continuous mapping from a topological space onto a subspace preserving points of that subspace, while deformation retract involves a homotopy between the identity map and the retraction, ensuring a stronger form of equivalence. Deformation retracts imply homotopy equivalence, making them crucial in algebraic topology for simplifying complex spaces without altering their fundamental group or homotopy type. Retractions may not preserve all homotopic properties, but deformation retracts guarantee topological invariants remain intact, highlighting the importance of deformation retracts in topological simplification and classification.
Retraction Infographic
 libterm.com
libterm.com