Real analysis explores the rigorous study of real numbers, sequences, series, and functions, laying the foundation for understanding continuity, limits, and integrability. Mastering these concepts sharpens your analytical skills and enhances problem-solving abilities in various mathematical and applied fields. Dive into the rest of the article to deepen your grasp of real analysis and its critical applications.
Table of Comparison
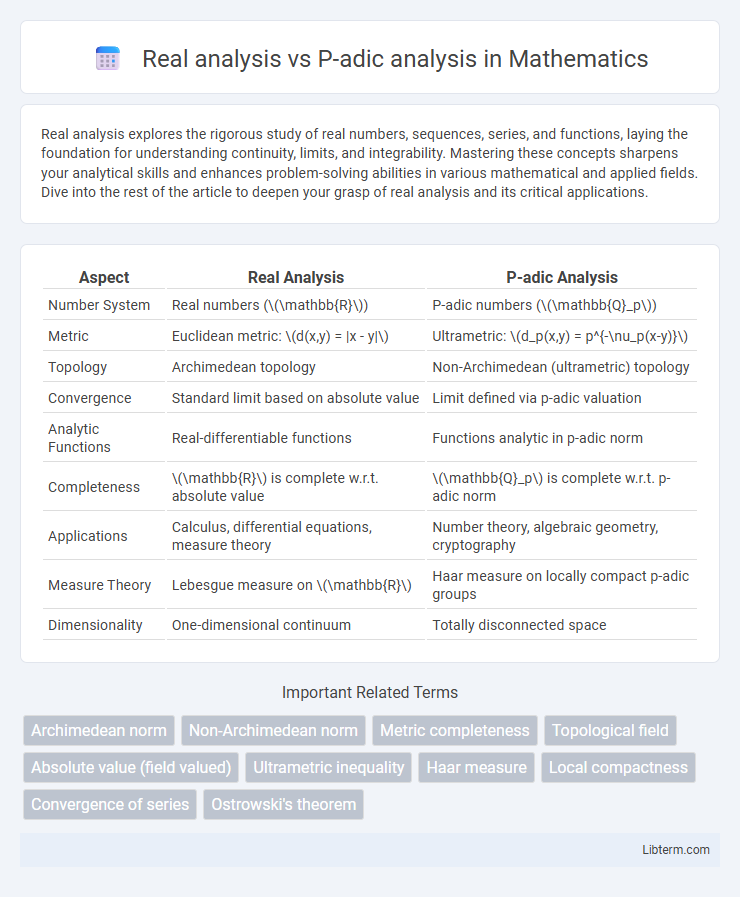
| Aspect | Real Analysis | P-adic Analysis |
|---|---|---|
| Number System | Real numbers (\(\mathbb{R}\)) | P-adic numbers (\(\mathbb{Q}_p\)) |
| Metric | Euclidean metric: \(d(x,y) = |x - y|\) | Ultrametric: \(d_p(x,y) = p^{-\nu_p(x-y)}\) |
| Topology | Archimedean topology | Non-Archimedean (ultrametric) topology |
| Convergence | Standard limit based on absolute value | Limit defined via p-adic valuation |
| Analytic Functions | Real-differentiable functions | Functions analytic in p-adic norm |
| Completeness | \(\mathbb{R}\) is complete w.r.t. absolute value | \(\mathbb{Q}_p\) is complete w.r.t. p-adic norm |
| Applications | Calculus, differential equations, measure theory | Number theory, algebraic geometry, cryptography |
| Measure Theory | Lebesgue measure on \(\mathbb{R}\) | Haar measure on locally compact p-adic groups |
| Dimensionality | One-dimensional continuum | Totally disconnected space |
Introduction to Real Analysis and P-adic Analysis
Real analysis studies the properties of real numbers, sequences, and functions with foundations in limits, continuity, differentiability, and integration in the real number system R. P-adic analysis, based on the p-adic number fields Q_p, explores analytic concepts through a non-Archimedean valuation, emphasizing series convergence and continuity in the p-adic topology. Both frameworks analyze functions and convergence but differ fundamentally in underlying metrics, with real analysis focused on the usual Euclidean norm and p-adic analysis on the p-adic norm dictated by prime p.
Foundations: Real Numbers vs. P-adic Numbers
Real analysis is grounded in the complete ordered field of real numbers, characterized by their Archimedean property and standard metric topology derived from the usual absolute value. P-adic analysis, by contrast, is founded on the field of p-adic numbers equipped with a non-Archimedean valuation determined by a prime number p, yielding an ultrametric space with fundamentally different notions of distance and convergence. These foundational differences in number systems lead to distinct analytical frameworks, where limits, continuity, and measure theory in real analysis do not directly translate to the p-adic context.
Topological Structures: Comparing Completeness
Real analysis and p-adic analysis differ fundamentally in their topological structures, notably in their notions of completeness. The real numbers are complete with respect to the usual Euclidean metric, meaning every Cauchy sequence converges within the real numbers. In contrast, the p-adic numbers form a complete metric space under the p-adic norm, characterized by a non-Archimedean valuation that induces an ultrametric topology, resulting in unique convergence properties distinct from real analysis.
Norms and Metrics: Absolute Value vs. P-adic Valuation
Real analysis employs the standard absolute value norm, which measures the distance between real numbers and satisfies the Archimedean property, ensuring familiar geometric intuitions. P-adic analysis, in contrast, uses the p-adic valuation as its norm, defining distance based on divisibility by a prime p and producing a non-Archimedean metric that leads to ultrametric spaces with unique topological features. These distinct norms fundamentally alter convergence, continuity, and completeness properties within their respective fields.
Convergence of Sequences and Series
Real analysis studies convergence of sequences and series based on the standard absolute value metric, where limits emerge from distances shrinking in the real number line. P-adic analysis examines convergence using the p-adic norm, which measures divisibility by a fixed prime p, leading to different notions of closeness and novel convergence criteria. Sequences that diverge in real analysis can converge p-adically, reflecting the non-Archimedean nature of the p-adic absolute value and resulting ultrametric topology.
Continuity and Differentiability in Both Analyses
Continuity in real analysis relies on the standard Euclidean metric, where a function f is continuous at point x if for every e>0 there exists d>0 such that |x-y| Lebesgue integration in real analysis extends the Riemann integral by measuring the size of sets to handle more complex functions and ensure convergence properties crucial in probability and functional analysis. P-adic integration, based on the topology of p-adic numbers, differs fundamentally as it integrates functions over fields with non-Archimedean valuations, often utilizing measures related to Haar measure on p-adic groups. Both theories serve to generalize integration but operate in distinct frameworks: Lebesgue integrates real-valued functions on real domains, while P-adic integration handles functions on ultrametric spaces with applications in number theory and arithmetic geometry. Real analysis plays a crucial role in number theory through tools like Fourier analysis and measure theory, aiding in solving Diophantine equations and understanding the distribution of prime numbers. P-adic analysis, leveraging the unique ultrametric properties of p-adic numbers, provides deep insights into congruences, local-global principles, and p-adic L-functions, essential for modern algebraic number theory and arithmetic geometry. Both frameworks extend beyond number theory into cryptography, signal processing, and dynamical systems by offering distinct approaches to continuity, convergence, and functional analysis. Real analysis studies the properties of real numbers, focusing on limits, continuity, and functions with respect to the standard absolute value norm. P-adic analysis, based on p-adic numbers, uses a non-Archimedean norm that changes convergence and topology, emphasizing ultrametric spaces and unique number expansions. Both frameworks analyze completeness, convergence, and continuity, but differ fundamentally in metric structures and applications in number theory versus classical calculus. Future directions in real analysis include exploring deeper connections with fractal geometry and advancing measure theory to address complex dynamical systems. P-adic analysis research focuses on refining applications in number theory and cryptography, particularly in understanding p-adic differential equations and their solutions. Open problems involve characterizing p-adic analogs of classical real analysis theorems and developing unified frameworks that bridge real and p-adic analytic techniques.Integration Theories: Lebesgue and P-adic Integration
Applications in Number Theory and Beyond
Key Differences and Similarities Summarized
Future Directions and Open Problems
Real analysis Infographic
 libterm.com
libterm.com