Cusp forms are a special class of modular forms characterized by their vanishing behavior at all cusps of a modular curve, playing a crucial role in number theory and the theory of automorphic functions. Their Fourier coefficients exhibit deep arithmetic significance, connecting areas like elliptic curves and L-functions. Explore the rest of the article to understand how cusp forms influence modern mathematical research and your studies.
Table of Comparison
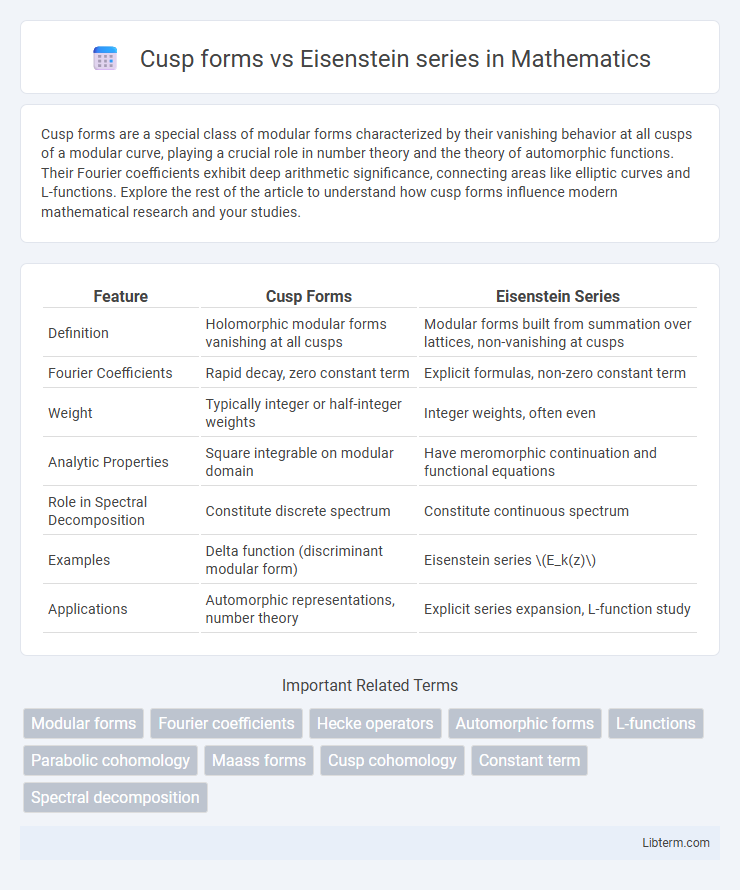
| Feature | Cusp Forms | Eisenstein Series |
|---|---|---|
| Definition | Holomorphic modular forms vanishing at all cusps | Modular forms built from summation over lattices, non-vanishing at cusps |
| Fourier Coefficients | Rapid decay, zero constant term | Explicit formulas, non-zero constant term |
| Weight | Typically integer or half-integer weights | Integer weights, often even |
| Analytic Properties | Square integrable on modular domain | Have meromorphic continuation and functional equations |
| Role in Spectral Decomposition | Constitute discrete spectrum | Constitute continuous spectrum |
| Examples | Delta function (discriminant modular form) | Eisenstein series \(E_k(z)\) |
| Applications | Automorphic representations, number theory | Explicit series expansion, L-function study |
Introduction to Modular Forms
Cusp forms and Eisenstein series are fundamental examples of modular forms, functions defined on the complex upper half-plane with transformation properties under the modular group. Eisenstein series are explicit, non-cuspidal modular forms characterized by their Fourier expansions containing constant terms, while cusp forms vanish at all cusps, reflecting deeper arithmetic properties. These distinctions play a crucial role in the spectral decomposition of spaces of modular forms, linking analytic behavior with number-theoretic structures.
Defining Cusp Forms
Cusp forms are holomorphic modular forms that vanish at all cusps of a modular curve, distinguishing them from Eisenstein series which exhibit nonzero constant terms at these points. The defining property of a cusp form is the rapid decay of its Fourier coefficients at infinity, ensuring its integral over a fundamental domain equals zero. This vanishing behavior at cusps underpins their critical role in the spectral decomposition of spaces of modular forms and their connections to L-functions.
Understanding Eisenstein Series
Eisenstein series are a class of modular forms characterized by their explicit Fourier expansions and non-vanishing constant terms, distinguishing them from cusp forms, which vanish at all cusps. These series serve as fundamental building blocks in the theory of modular forms, providing analytic continuations and connections to L-functions. Understanding Eisenstein series is crucial for exploring the spectral decomposition of automorphic forms and their role in number theory and arithmetic geometry.
Structural Differences Between Cusp Forms and Eisenstein Series
Cusp forms vanish at all cusps of the modular curve, ensuring rapid decay in their Fourier expansions, while Eisenstein series exhibit non-zero constant terms reflecting their growth at cusps. Structurally, cusp forms belong to the space of square-integrable modular forms with zero constant coefficients, contrasting with Eisenstein series, which serve as explicit examples of non-cuspidal modular forms constructed from summations over lattice points. This fundamental difference shapes their role in the spectral decomposition of automorphic forms and influences their arithmetic properties and applications in number theory.
Fourier Expansions: Contrasting Behaviors
Cusp forms exhibit Fourier expansions with coefficients that vanish at zero frequency, reflecting their rapid decay and orthogonality to Eisenstein series. Eisenstein series display Fourier expansions containing constant terms and non-decaying coefficients, embodying their role as non-cuspidal automorphic forms. This stark contrast in Fourier behavior underscores the fundamental differences in their spectral contributions to modular form theory.
Analytical Properties and Growth Rates
Cusp forms exhibit rapid decay at cusps, ensuring their Fourier coefficients vanish at infinity, which leads to square-integrability and moderate growth rates in the upper half-plane. Eisenstein series display slower growth, characterized by a constant term in their Fourier expansion that causes them to fail square-integrability but allows meromorphic continuation and analytic continuation across the complex plane. The contrasting growth rates and analytic properties underpin their distinct roles in the spectral decomposition of automorphic forms and in the formulation of Langlands' program.
Role in the Spectral Decomposition of Modular Forms
Cusp forms and Eisenstein series play distinct roles in the spectral decomposition of modular forms, where cusp forms constitute the discrete spectrum associated with square-integrable automorphic forms and exhibit rapid decay at cusps. Eisenstein series form the continuous spectrum, arising from parabolic induction and encoding scattering phenomena, essential for understanding the non-compactness of modular curves. The interplay between these components allows for a complete Plancherel-type decomposition of the space of modular forms, crucial in analytic number theory and the study of L-functions.
Arithmetic Significance and L-functions
Cusp forms play a crucial role in the theory of modular forms as they vanish at all cusps and their Fourier coefficients encode deep arithmetic information, particularly relating to eigenvalues of Hecke operators and connections to elliptic curves. Eisenstein series, characterized by their explicit Fourier expansions, contribute to the constant term and relate directly to special values of L-functions, such as the Riemann zeta function and Dirichlet L-series. The interplay between cusp forms and Eisenstein series within the spectral decomposition of modular forms underpins profound results in number theory, including the formulation of the Langlands program and the analytic properties of automorphic L-functions.
Examples Illustrating Cusp Forms and Eisenstein Series
Cusp forms, such as the Ramanujan Delta function D(z), vanish at all cusps of the modular group and exhibit rapid decay towards the cusps, making them essential in the space of modular forms with zero constant term in their Fourier expansions. Eisenstein series, exemplified by the classical Eisenstein series \( E_k(z) \) for even weight \( k \geq 4 \), are non-cuspidal modular forms characterized by their explicit Fourier expansions with non-zero constant terms, generating the Eisenstein subspace. Both examples highlight fundamental differences: cusp forms generate the cusp subspace orthogonal to Eisenstein series, which form the complementary subspace in the modular forms space for congruence subgroups like \( SL(2,\mathbb{Z}) \).
Applications and Further Research Directions
Cusp forms play a crucial role in number theory and automorphic representations, particularly in the proof of modularity theorems and the Langlands program, while Eisenstein series are fundamental in understanding spectral decompositions and L-functions. Applications of cusp forms include cryptographic algorithms and arithmetic geometry, as they encode deep arithmetic information through their Fourier coefficients. Further research explores the interplay between these functions in analytic number theory, quantum chaos, and the development of new automorphic lifting techniques to address unsolved problems in arithmetic.
Cusp forms Infographic
 libterm.com
libterm.com