A circle is a fundamental geometric shape defined by all points equidistant from a central point, creating a perfectly symmetrical curve. Understanding its properties, such as radius, diameter, circumference, and area, is essential for solving various mathematical and real-world problems. Explore the rest of the article to deepen your knowledge of circles and their applications.
Table of Comparison
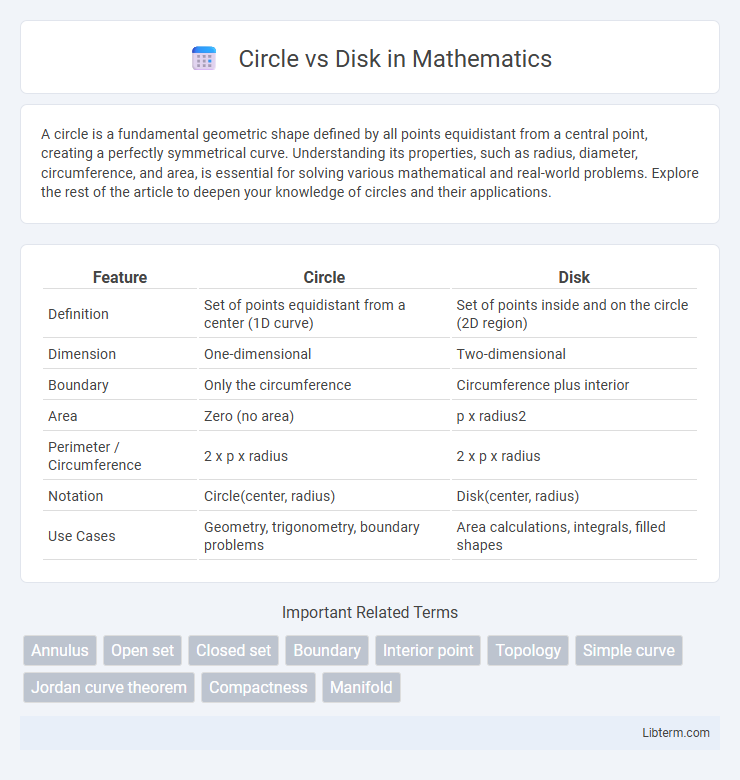
| Feature | Circle | Disk |
|---|---|---|
| Definition | Set of points equidistant from a center (1D curve) | Set of points inside and on the circle (2D region) |
| Dimension | One-dimensional | Two-dimensional |
| Boundary | Only the circumference | Circumference plus interior |
| Area | Zero (no area) | p x radius2 |
| Perimeter / Circumference | 2 x p x radius | 2 x p x radius |
| Notation | Circle(center, radius) | Disk(center, radius) |
| Use Cases | Geometry, trigonometry, boundary problems | Area calculations, integrals, filled shapes |
Introduction to Circles and Disks
A circle is defined as the set of all points in a plane equidistant from a fixed center point, forming a one-dimensional curve. A disk includes the circle and all points inside it, representing a two-dimensional region bounded by the circle. Understanding the distinction between a circle as a boundary and a disk as a filled area is fundamental in geometry and topology.
Defining Circles: Key Characteristics
A circle is a set of all points in a plane equidistant from a fixed center point, characterized by its constant radius. The key characteristics of a circle include the center, radius, diameter, and circumference, which define its geometric properties. Unlike a disk, which includes all points inside the boundary, a circle refers strictly to the continuous curve forming the boundary itself.
What is a Disk? Essential Features
A disk is a two-dimensional geometric shape consisting of all points in a plane that lie within a fixed distance, called the radius, from a central point known as the center. It includes both the boundary, which is the circle itself, and every point inside that boundary, making it a filled-in area rather than just a curve. Essential features of a disk include its radius, center, area calculated as p times the radius squared, and the property of being a convex and compact set in Euclidean geometry.
Mathematical Representation: Circle vs Disk
A circle is mathematically defined as the set of points equidistant from a central point in a plane, represented by the equation (x - h)2 + (y - k)2 = r2, where (h, k) is the center and r is the radius. A disk, in contrast, includes all the points inside and on the boundary of the circle, expressed by the inequality (x - h)2 + (y - k)2 <= r2. The distinction is crucial in geometry and analysis, where the circle represents a one-dimensional curve, while the disk denotes a two-dimensional region.
Geometric Differences Explained
A circle is a one-dimensional curve consisting of all points equidistant from a center point, defined by its radius, whereas a disk is a two-dimensional region that includes the circle and all points inside it. The geometric difference lies in the circle representing only the boundary line, while the disk encompasses the entire area enclosed by the circle. This distinction is fundamental in topology and geometry, affecting calculations of perimeter for the circle and area for the disk.
Applications of Circles in Real Life
Circles play a crucial role in various real-life applications such as engineering, architecture, and technology, where their geometric properties facilitate the design of gears, wheels, and circular tracks. Unlike disks, which include the interior area, circles are primarily used to define boundaries and create precise measurements in fields like navigation and construction. The inherent symmetry and constant radius of circles enable efficient motion and structural stability in mechanical systems and urban planning.
Disk Usage in Geometry and Beyond
Disk usage in geometry extends beyond the simple area of a circle, encompassing considerations in complex plane analysis and topology where disks represent closed regions including their boundary. The term "disk" indicates a filled circle, crucial in computational geometry for algorithms involving spatial coverage, collision detection, and optimization problems. Its applications reach into physics and computer graphics, where understanding disk usage aids in modeling surfaces and volumes accurately.
Visualizing Circles and Disks
Visualizing circles involves representing the set of points equidistant from a fixed center, forming a one-dimensional boundary with zero area. Disks, in contrast, include all points within the circle's boundary, creating a two-dimensional region with measurable area. Graphically, circles appear as simple outlines while disks are depicted as filled-in shapes, emphasizing their interior content.
Common Confusions: Circle vs Disk
Circle and disk are often confused because both involve round shapes, but a circle refers only to the set of all points equidistant from a center point, representing the boundary. A disk includes everything inside the circle's boundary, encompassing the entire area enclosed by the circle. Understanding this distinction is essential in geometry, where a circle is one-dimensional and a disk is two-dimensional.
Summary: Choosing Between Circle and Disk
Selecting between a circle and a disk depends on whether you require just the boundary or the entire area it encloses. A circle refers to the one-dimensional curve consisting of all points equidistant from the center, while a disk includes the circle and every point inside it, representing a two-dimensional shape. For applications involving perimeter or edge properties, use a circle; for area calculations or filled shapes, opt for a disk.
Circle Infographic
 libterm.com
libterm.com