A solvable group is a type of group in abstract algebra characterized by a series of subgroups where each is normal in the next, and the quotient groups are abelian. This property makes solvable groups crucial in understanding the structure of more complex groups and in areas like Galois theory. Discover why solvable groups matter and how they influence your study of algebra in the rest of this article.
Table of Comparison
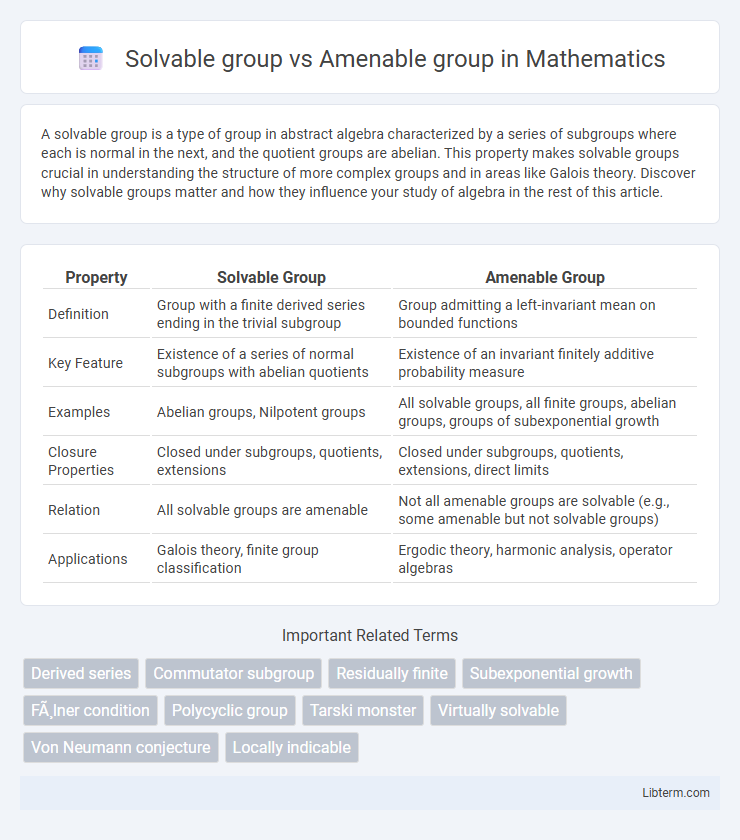
| Property | Solvable Group | Amenable Group |
|---|---|---|
| Definition | Group with a finite derived series ending in the trivial subgroup | Group admitting a left-invariant mean on bounded functions |
| Key Feature | Existence of a series of normal subgroups with abelian quotients | Existence of an invariant finitely additive probability measure |
| Examples | Abelian groups, Nilpotent groups | All solvable groups, all finite groups, abelian groups, groups of subexponential growth |
| Closure Properties | Closed under subgroups, quotients, extensions | Closed under subgroups, quotients, extensions, direct limits |
| Relation | All solvable groups are amenable | Not all amenable groups are solvable (e.g., some amenable but not solvable groups) |
| Applications | Galois theory, finite group classification | Ergodic theory, harmonic analysis, operator algebras |
Introduction: Understanding Solvable and Amenable Groups
Solvable groups are algebraic structures characterized by a finite series of subgroups where each is normal in the next, and the successive quotient groups are abelian, revealing a layered composition conducive to analysis. Amenable groups extend this concept by possessing an invariant mean on bounded functions, facilitating the study of harmonic analysis and ergodic theory through measures that remain stable under group actions. Understanding the distinction between solvable and amenable groups provides insight into their respective roles in group theory, functional analysis, and topology.
Defining Solvable Groups: Key Concepts
Solvable groups represent a class of groups whose structure can be analyzed through a finite sequence of subgroups, each normal in the next, with successive quotient groups that are abelian. This hierarchical decomposition, known as the derived series, terminates in the trivial group, reflecting the group's solvability. Distinct from amenable groups, solvable groups emphasize algebraic conditions related to commutator subgroups rather than measure-theoretic properties like invariant means.
Defining Amenable Groups: An Overview
Amenable groups are defined by the existence of a left-invariant mean on bounded functions, reflecting a measure-theoretic notion of "averageability" that generalizes finite groups and abelian groups. Unlike solvable groups, which are characterized by a series of subgroups with abelian quotients, amenable groups encompass a broader class including all solvable groups, nilpotent groups, and groups of subexponential growth. This property ensures that amenable groups do not contain paradoxical decompositions, a key distinction from non-amenable groups often studied in geometric group theory and operator algebras.
Historical Development and Motivation
Solvable groups emerged from early studies in Galois theory and polynomial equations, aiming to classify groups whose structure could be broken down via a sequence of abelian quotients. Amenable groups were introduced later by John von Neumann in 1929 to address the Banach-Tarski paradox, characterizing groups with invariant means that prevent paradoxical decompositions. The historical development of these concepts reflects distinct motivations: solvable groups prioritize algebraic decomposition related to solvability of equations, whereas amenable groups focus on measure-theoretic properties and group actions in analysis.
Fundamental Differences Between Solvable and Amenable Groups
Solvable groups are characterized by a finite derived series terminating in the trivial subgroup, emphasizing their algebraic structure through iterative commutator subgroups. Amenable groups, however, are defined by the existence of an invariant mean on bounded functions, reflecting a measure-theoretic property related to averaging and fixed points. The fundamental difference lies in solvability focusing on group composition and normal subgroups, while amenability centers on group actions and invariance under averaging processes.
Examples of Solvable Groups
Solvable groups include all finite abelian groups and the symmetric group S_3, with their derived series terminating in the trivial subgroup. Examples also encompass nilpotent groups such as the Heisenberg group and certain matrix groups over fields with triangular form. These examples contrast with amenable groups, which include all solvable groups but extend to groups like free abelian groups and some infinite groups beyond solvable classifications.
Examples of Amenable Groups
Amenable groups include all solvable groups, such as abelian groups and finite groups, which exhibit the Folner condition indicating amenability. Examples also extend to groups containing sub-exponential growth, like the Heisenberg group and nilpotent groups, known for their invariant means. In contrast, free groups on two or more generators are non-amenable, highlighting the distinct boundary between amenability and solvability in group theory.
Intersection: When Are Solvable Groups Amenable?
Solvable groups are always amenable because they have a finite derived series terminating in the trivial subgroup, allowing for the construction of invariant means. Amenable groups include all solvable groups, as their algebraic structure prevents paradoxical decompositions characteristic of non-amenable groups. The intersection occurs inherently since every solvable group satisfies the Folner criterion for amenability, making all solvable groups amenable by definition.
Applications in Mathematics and Related Fields
Solvable groups play a crucial role in Galois theory and the classification of polynomial equations, enabling solutions via radicals by decomposing groups into abelian subgroups. Amenable groups are fundamental in ergodic theory and harmonic analysis, providing tools for analyzing invariant means and Folner sequences in dynamical systems. Both concepts find applications in geometric group theory and operator algebras, where solvability aids in structural decomposition and amenability impacts measure-theoretic properties.
Conclusion: Comparing Solvable and Amenable Group Structures
Solvable groups are characterized by a finite derived series terminating in the trivial subgroup, highlighting their structured and hierarchical nature often linked to algebraic solvability. Amenable groups encompass a broader class, including all solvable groups but extending to groups with invariant means, reflecting properties related to measure theory and harmonic analysis. Comparing these structures reveals that while all solvable groups are amenable, amenable groups include non-solvable examples, indicating a fundamental generalization in the study of group properties.
Solvable group Infographic
 libterm.com
libterm.com