Scaling is essential for businesses aiming to grow efficiently without compromising quality or performance. It involves expanding resources, processes, and systems to handle increased demand seamlessly. Discover how effective scaling strategies can transform your business by reading the rest of the article.
Table of Comparison
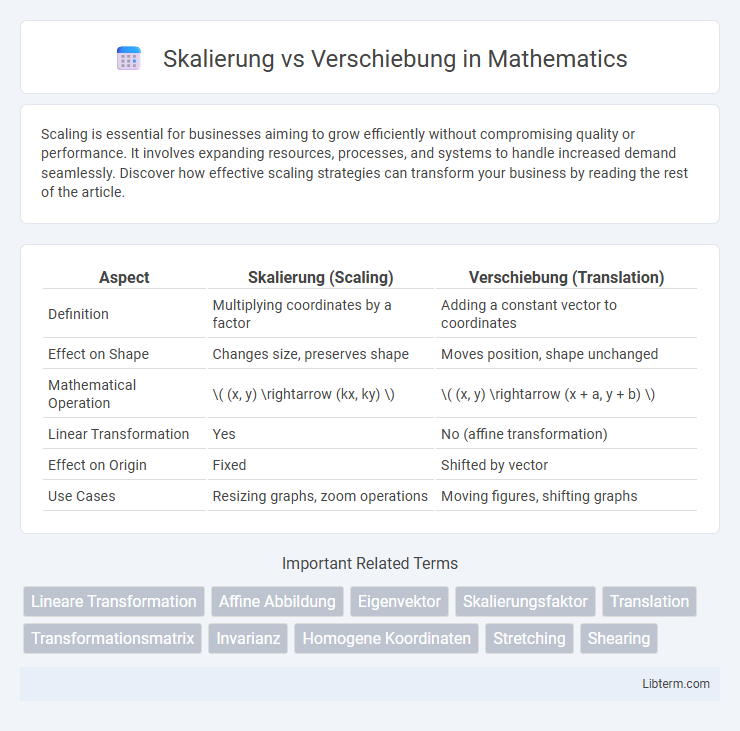
| Aspect | Skalierung (Scaling) | Verschiebung (Translation) |
|---|---|---|
| Definition | Multiplying coordinates by a factor | Adding a constant vector to coordinates |
| Effect on Shape | Changes size, preserves shape | Moves position, shape unchanged |
| Mathematical Operation | \( (x, y) \rightarrow (kx, ky) \) | \( (x, y) \rightarrow (x + a, y + b) \) |
| Linear Transformation | Yes | No (affine transformation) |
| Effect on Origin | Fixed | Shifted by vector |
| Use Cases | Resizing graphs, zoom operations | Moving figures, shifting graphs |
Skalierung vs Verschiebung: Definitionen und Grundlagen
Skalierung bezeichnet in der Mathematik eine Transformation, bei der Grossenverhaltnisse eines Objekts proportional verandert werden, wahrend die Form erhalten bleibt. Verschiebung beschreibt die Translation eines Objekts entlang einer bestimmten Richtung ohne Veranderung von Grosse oder Form. Beide Konzepte sind grundlegende Transformationen in der linearen Algebra und Geometrie, entscheidend fur Bildmanipulationen und Koordinatentransformationen.
Mathematische Prinzipien hinter Skalierung und Verschiebung
Skalierung und Verschiebung sind fundamentale Transformationen in der linearen Algebra und der Geometrie, wobei Skalierung die Multiplikation von Vektoren oder Koordinaten mit einem Skalierungsfaktor beschreibt, der Grossenanderungen ohne Richtungswechsel bewirkt. Verschiebung, auch als Translation bekannt, verschiebt Punkte oder Objekte entlang eines Vektors durch Addition eines Verschiebungsvektors, wodurch die Form erhalten bleibt, jedoch die Position verandert wird. Mathematisch basiert Skalierung auf der Anwendung linearer Transformationen mit diagonalen Skalierungs-Matrizen, wahrend Verschiebung durch die Addition eines konstanten Vektors zu jedem Punkt realisiert wird.
Anwendungen in der Datenverarbeitung
Skalierung und Verschiebung sind grundlegende Transformationen in der Datenverarbeitung, die zur Normalisierung und Standardisierung von Datensatzen verwendet werden. Skalierung passt die Wertebereiche an, haufig durch Min-Max-Skalierung oder Z-Score-Normalisierung, um Merkmale vergleichbar zu machen und Algorithmen wie maschinelles Lernen zu optimieren. Verschiebung verschiebt Datenpunkte entlang der Achsen, wodurch der Ursprung der Daten variiert und beispielsweise bei der Zentrierung von Daten fur PCA-Analyse oder Zeitreihenmodellen relevant wird.
Skalierung vs Verschiebung in der Graphischen Darstellung
Skalierung in der graphischen Darstellung verandert die Grosse eines Objekts durch Multiplikation seiner Koordinaten mit einem Skalierungsfaktor, wodurch Proportionen und Abstande angepasst werden. Verschiebung hingegen verschiebt ein Objekt um einen festen Vektor, wobei alle Punkte gleichmassig entlang einer Achse oder in mehreren Richtungen translatiert werden, ohne Form oder Grosse zu verandern. Skalierung beeinflusst somit die Dimensionen und Verhaltnisse eines Graphen, wahrend Verschiebung lediglich die Position im Koordinatensystem verandert.
Einfluss auf statistische Analysen
Skalierung verandert die Streuung und Varianz von Daten, was direkte Auswirkungen auf die Standardabweichung und Regressionskoeffizienten in statistischen Modellen hat. Verschiebung hingegen beeinflusst den Mittelwert, ohne die Varianz oder Korrelationen zwischen Variablen zu verandern, wodurch die Struktur der Daten intakt bleibt. Bei der Datenvorbereitung fur multivariate Analysen ist es entscheidend, Skalierung zu berucksichtigen, da sie Distanzmessungen und Gewichtungen in Algorithmen wie PCA oder Clusteranalysen beeinflusst.
Praktische Beispiele aus der Technik
Skalierung verandert die Grosse von Objekten oder Signalen, etwa in der Bildverarbeitung, wo Bilder vergrossert oder verkleinert werden, ohne das Bildformat zu andern. Verschiebung verschiebt Positionen oder Wertebereiche, wie bei der Kalibrierung von Sensoren, um Messwerte zu justieren. In der Robotik werden Skalierung und Verschiebung kombiniert, um Trajektorien anzupassen und prazise Bewegungen zu ermoglichen.
Vorteile und Herausforderungen beider Methoden
Skalierung ermoglicht die Anpassung von Daten durch Multiplikation, was die Veranderung der Grossenordnung ohne Verlust der relativen Abstande bewirkt und besonders vorteilhaft bei der Normalisierung ist. Verschiebung verschiebt Daten durch Addition oder Subtraktion eines konstanten Wertes, was die Position der Werte ohne Beeintrachtigung der Verteilung verandert, ideal fur das Zentrieren von Daten. Herausforderungen bei Skalierung liegen in der Sensitivitat gegenuber Ausreissern, wahrend Verschiebung keine Anderung der Streuung bewirkt und daher bei unterschiedlichen Varianzen weniger flexibel ist.
Skalierung und Verschiebung in der Bildverarbeitung
Skalierung in der Bildverarbeitung verandert die Grosse eines Bildes durch Anpassung der Pixelanzahl, ohne die Bildinhalte zu verzerren, wobei Interpolationsmethoden wie Bilinear- oder Bikubikinterpolation zur glatten Skalierung eingesetzt werden. Verschiebung bezieht sich auf die Translation des Bildes im Koordinatensystem, wodurch Bildinformationen um eine bestimmte Distanz horizontal und/oder vertikal verschoben werden, ohne Grosse oder Form zu verandern. Kombinationen aus Skalierung und Verschiebung ermoglichen prazise geometrische Transformationen fur Anwendungen wie Bildregistrierung, Objekterkennung und Grafikanpassungen.
Relevanz für maschinelles Lernen
Skalierung (Scaling) normalizes feature ranges to improve convergence speed and model accuracy in machine learning algorithms like gradient descent and SVMs. Verschiebung (Translation) centers data by adjusting mean values, enhancing stability and interpretability in neural networks and PCA. Proper application of both transformations ensures balanced feature contributions, preventing bias and improving predictive performance.
Fazit: Wann Skalierung, wann Verschiebung?
Skalierung eignet sich besonders zur Veranderung der Grosse oder Intensitat eines Objekts oder Signals, wahrend Verschiebung zur Anpassung der Position oder des Ausgangspunkts verwendet wird. Skalierung wird haufig angewandt, wenn relative Proportionen erhalten bleiben sollen, etwa bei der Bildvergrosserung oder Signalverstarkung; Verschiebung hingegen ist sinnvoll bei der Justierung von Startpunkten in Zeitreihen oder Koordinatensystemen. Die Wahl zwischen Skalierung und Verschiebung hangt somit von der Zielsetzung ab: Grossenanpassung versus Positionskorrektur.
Skalierung Infographic
 libterm.com
libterm.com