The prime spectrum of a ring, denoted as Spec(R), is the set of all prime ideals of the ring equipped with the Zariski topology, serving as a fundamental object in algebraic geometry and commutative algebra. It provides a geometric way to study ring properties through topological and algebraic tools, linking algebraic structures with geometric intuition. Explore the rest of the article to delve deeper into the significance and applications of the prime spectrum in modern mathematics.
Table of Comparison
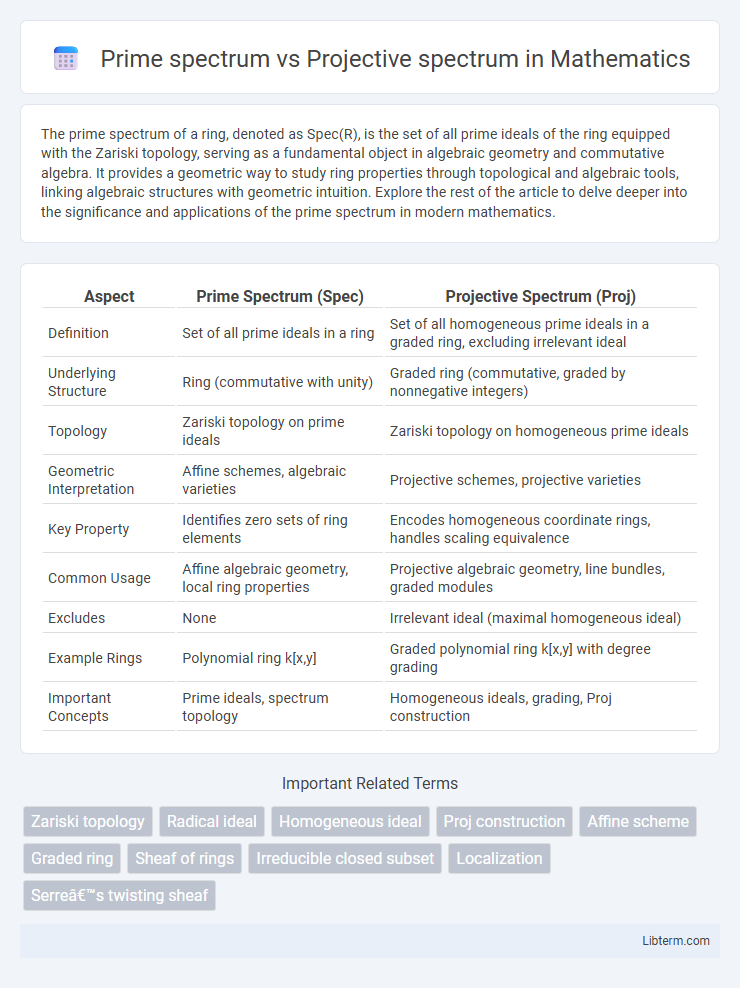
| Aspect | Prime Spectrum (Spec) | Projective Spectrum (Proj) |
|---|---|---|
| Definition | Set of all prime ideals in a ring | Set of all homogeneous prime ideals in a graded ring, excluding irrelevant ideal |
| Underlying Structure | Ring (commutative with unity) | Graded ring (commutative, graded by nonnegative integers) |
| Topology | Zariski topology on prime ideals | Zariski topology on homogeneous prime ideals |
| Geometric Interpretation | Affine schemes, algebraic varieties | Projective schemes, projective varieties |
| Key Property | Identifies zero sets of ring elements | Encodes homogeneous coordinate rings, handles scaling equivalence |
| Common Usage | Affine algebraic geometry, local ring properties | Projective algebraic geometry, line bundles, graded modules |
| Excludes | None | Irrelevant ideal (maximal homogeneous ideal) |
| Example Rings | Polynomial ring k[x,y] | Graded polynomial ring k[x,y] with degree grading |
| Important Concepts | Prime ideals, spectrum topology | Homogeneous ideals, grading, Proj construction |
Introduction to Algebraic Spectra
The prime spectrum of a ring, denoted Spec(R), consists of all prime ideals equipped with the Zariski topology, serving as a fundamental tool in algebraic geometry to study ring structures via geometric methods. The projective spectrum, Proj(R), extends this concept to graded rings, focusing on homogeneous prime ideals and providing a framework for constructing projective varieties and schemes. Both spectra translate algebraic properties into geometric language but differ in their applicability: Spec handles affine schemes, while Proj handles projective schemes, reflecting the graded nature of polynomial rings in geometry.
Defining the Prime Spectrum (Spec)
The prime spectrum (Spec) of a ring R is the set of all prime ideals of R, equipped with the Zariski topology, where closed sets correspond to the vanishing of sets of ring elements. Spec serves as a fundamental object in algebraic geometry, capturing algebraic properties of R through geometric points identified with prime ideals. In comparison, the projective spectrum (Proj) generalizes this construction to graded rings, focusing on homogeneous prime ideals and providing the foundation for projective schemes.
Understanding the Projective Spectrum (Proj)
The projective spectrum (Proj) generalizes the prime spectrum (Spec) by focusing on graded rings and homogeneous prime ideals, which provide a natural framework for studying projective varieties in algebraic geometry. Unlike Spec, which considers all prime ideals of a ring, Proj restricts attention to homogeneous primes excluding the irrelevant ideal, enabling the construction of schemes that correspond to projective spaces. Understanding Proj involves grasping the connection between graded ring structures and geometric objects, facilitating the translation from algebraic data to projective geometric intuition.
Topological Structures in Spec and Proj
The prime spectrum (Spec) of a ring is equipped with the Zariski topology, where closed sets correspond to vanishing sets of ideals, making it a sober and spectral space fundamental in algebraic geometry. The projective spectrum (Proj) construction refines Spec by considering homogeneous prime ideals in a graded ring, endowed with a topology induced by the irrelevant ideal, yielding a projective scheme with a structure sheaf supporting homogeneous localization. Both Spec and Proj possess underlying spectral topologies satisfying Hochster's axioms, but Proj's topology encodes additional grading data crucial for studying projective varieties and sheaf cohomology in graded contexts.
Affine vs Projective Schemes
The prime spectrum (Spec) of a ring defines an affine scheme by associating prime ideals with geometric points, providing a local description of algebraic varieties. In contrast, the projective spectrum (Proj) of a graded ring constructs projective schemes, capturing global projective geometry through homogeneous prime ideals and accounting for the grading structure. Affine schemes correspond to "classical" algebraic varieties with a simpler local viewpoint, while projective schemes generalize this concept to include compactifications and embeddings into projective space, essential for studying global geometric properties.
Points and Closed Sets in Spec and Proj
In the prime spectrum (Spec) of a ring, points correspond to prime ideals, with the Zariski topology defined by closed sets V(I) consisting of all primes containing the ideal I. In the projective spectrum (Proj) of a graded ring, points correspond to homogeneous prime ideals not containing the irrelevant ideal, and closed sets are defined similarly by homogeneous ideals, reflecting the graded structure. The distinction in their point sets and closed sets arises from the grading in Proj, which filters out non-relevant primes and leads to a richer geometric interpretation in projective algebraic geometry.
Relations to Commutative Rings and Graded Rings
The prime spectrum of a commutative ring, denoted Spec(R), consists of all prime ideals and forms a topological space fundamental in algebraic geometry, encapsulating the ring's algebraic structure. The projective spectrum, Proj(R), applies to graded rings and parametrizes homogeneous prime ideals not containing the irrelevant ideal, leading to the construction of projective schemes. Both spectra serve as bridges from algebraic properties of rings to geometric objects, with Spec linking general commutative rings to affine schemes and Proj connecting graded rings to projective geometry.
Morphisms between Spec and Proj
Morphisms between the prime spectrum Spec(R) and the projective spectrum Proj(S) reflect the fundamental differences in their algebraic structures: Spec(R) classifies prime ideals of a ring R, while Proj(S) parametrizes homogeneous prime ideals of a graded ring S. A morphism from Spec(R) to Proj(S) corresponds to a graded ring homomorphism from S to a suitable graded ring extension of R, ensuring compatibility with the grading and preserving the relevant ideal structures. These morphisms induce continuous maps underlying the functorial relationships, crucial for translating geometric properties between affine schemes and projective schemes in algebraic geometry.
Applications in Algebraic Geometry
The prime spectrum, Spec(R), serves as the foundational space in algebraic geometry by encoding the prime ideals of a ring R, enabling the study of affine schemes and their morphisms. The projective spectrum, Proj(R), extends this framework to graded rings, allowing construction of projective schemes crucial for analyzing projective varieties and homogeneous coordinate rings. Both spectra facilitate the translation of algebraic properties into geometric contexts, with Spec(R) applying primarily to affine varieties and Proj(R) to projective varieties, underpinning core concepts such as sheaf cohomology and scheme theory in modern algebraic geometry.
Key Differences and Comparative Analysis
Prime spectrum (Spec) of a ring consists of all prime ideals, forming a topological space with the Zariski topology, essential in algebraic geometry to study algebraic varieties. Projective spectrum (Proj) deals with graded rings, specifically homogeneous prime ideals not containing the irrelevant ideal, crucial for constructing projective schemes and studying graded ring structures. The key difference lies in Spec focusing on arbitrary prime ideals for affine schemes, while Proj emphasizes graded structure for projective geometry, with Spec capturing local properties and Proj encoding global projective data.
Prime spectrum Infographic
 libterm.com
libterm.com